分层抽样下样本量的分配方法研究

李林蔓

（重庆第二师范学院 旅游与服务管理系，重庆 400067）

0 引言

分层抽样是在概率抽样中非常常用的样本抽样方法。分层抽样中所采取第一种方法是按比例缩小来确定样本单位数结构，这是最简单可行的分配方式。但大多数人认为除遵循样本与总体单位数结构一致性外。还必须考虑总体不同层次方差的差异。满足抽样估计量方差的最小化要求，简而言之，就是指在有限资金、时间或其他与每层的样本分配量相关的条件限制下，分配每层的样本量使估计量方差最小。

统计抽样检验的理论自1924年由美国贝尔实验室的罗米格博士和道吉博士提出后，多年来在实践中不断完善和发展，而且还在发展之中。我国学者对分层抽样方法的研究有很多。王晓燕[1]等借助了非线性规划和非线性目标规划等最优化方法，试图解决实际中遇到的问题，以解决简单分层抽样的不足。范雯雯[2]利用分层方法，通过选择适当的期权,对使用方差减缩技术和没有使用方差减缩技术的期权价格进行比较,发现使用方差减缩技术期权的精度更高,并且使用方差差减缩技术后,标准差更小,那么模拟出的期权价格可信度就更高了。邱赛兵[3]等为多项选择敏感性问题提供科学的、精度更高的随机抽样调查方法及其统计量的计算公式,设计出多项选择敏感问题分层抽样下的随机抽样调查模型,并推导出在此模型下总体比例的估计量及其估计方差的计算公式,计算出敏感属性比例95%的置信区间。分层抽样需将研究总体组合成一个个层，然后再在每一层选取一个随机样本。使用分层抽样的目的不外乎以下几个：确保每一层的比例有代表性；降低抽样变异性；使较小的子总体能从而使分析更为可靠。

综上文献发现，对分层抽样的研究集中在样本选择的方法和置信区间的空政等，比例分层抽样和非比例分层抽样只作为一种工具被大家使用，还没有学者对比例分层抽样和非比例分层抽样进行具体的分析比较。比例分层抽样是指按各个层的单位数量占调查总体单位数量的比例分配各层的样本数量的。在分层抽样中，采用分层比例抽样可以提高样本的代表性，及对总体数量指标的估计值的确定，避免出现简单随机抽样中的集中于某些特性或遗漏掉某些特性。但是在现实样本收集的过程中，样本并不规范，并不是所有的样本都能使用比例分层抽样。本文将以母亲文化程度分层的考试分数比例分层样本为实例介绍比例分层抽样和不成比例分层抽样的方法。

1 样本来源

分层抽样可以是成比例的，也可以不是成比例的。成比例的分层抽样的目的在于在每一层中用相同的抽样分数来保证层的比例的代表性。本文调查了某高校的15名学生，以研究母亲文化程度对学生成绩的影响。将母亲文化程度分为高中以下、高中和大学肄业和大学三个层次，抽样后统计学生的成绩，如表1所示。这一变量被认为是知识技巧的一个重要的预测变量，因而保证样本能在这一变量上按比例地代表三个组是很重要的。

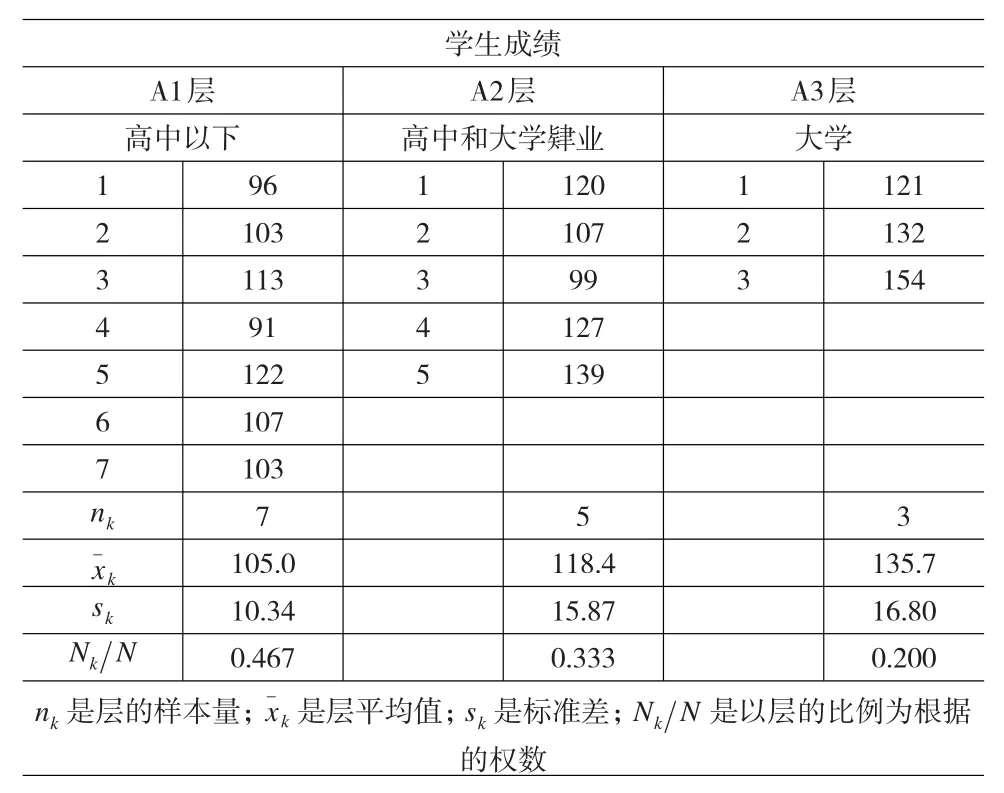
表1 按母亲文化程度分层的考试分数比例分层样本

2 比例分层抽样实例

在使用比例分层抽样时，因为每一层包含的成员数目不同，所以每一层的样本的容量，如表1所示也不同。对于比例分层抽样来讲，每一层的抽样分数都是相同的。它的均值、比例和其他统计量的计算公式与简单随机抽样都是一样的。

表2 分层抽样标准差计算法：以比例分成样本为例

分层可以减少标准误差，这一点可以用这一例子的未作分层数据，且使用用于简单随机样本公式计算的标准误差得到证明。分层样本的标准误差与简单随机样本的标准误差的比率就是设计效应(deft)的平方根，设计效应的值列在了该表的底部。就这一例子而言，精度的相对增益是21%(100%一79%)。

表4将备择的分层变量班级用于与表2表3相同的总体。这一分层的增益为2%，它等于设计效应的平方根，小于用母亲的文化程度分层的增益。班级分层的设计效应的平方根为98%，而用母亲的文化程度分层的是79%。母亲的文化程度较之学生就读的班级解释了更多的学生考试成绩的方差。比较这两个例子，我们不难发现，用母亲文化程度分层的各层均值的间距(30．7)，大于用班级分层的均值间距(16.0)。不仅如此，我们还可以看到，用母亲文化程度分层的层内变差或标准差(s)都比较小。

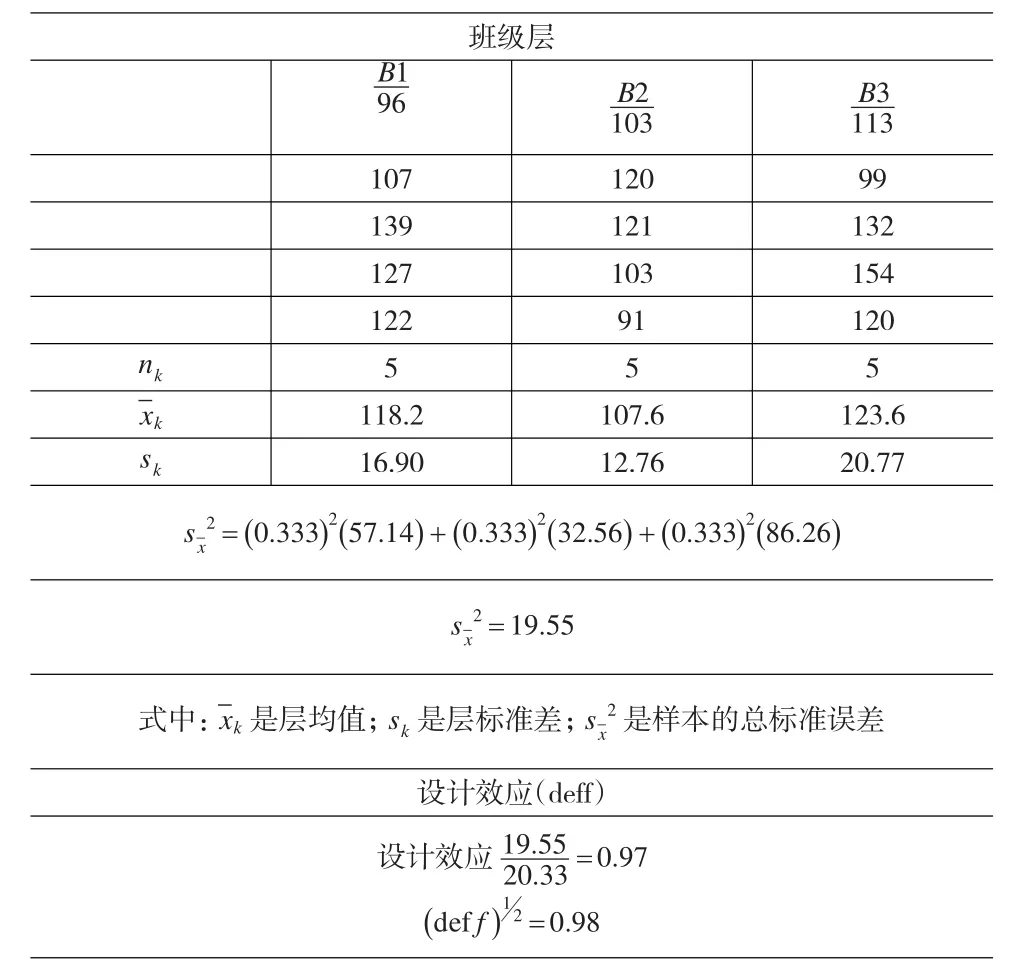
表4 分层样本标准误差计算法：以备择比例分层为例

从以上可以得出，层所占比例的大小(删)会对相对增益有所影响。增加某一小子总体的样本量，不论它与总体的其余部分有多么大的不同，也不会显著改善估计的精度。在百分比或比例是分析的主要目标时，分层的增益一般都不会太大。在层内的变差较小(同质)和层间的差别比较大的时候，分层就会有比较大的斩获。一般讲，在层与层之间的大小比例差别很大时，很难通过分层来提高估计值的精度。

3 不成比例分层抽样实例

当在遇到整个样本的精度，或某个子总体的精度不够这样的情况的时候，可以改而采用不成比例的分层。不成比例的分层源于对不同的层使用不同的抽样分数。采用不同的抽样分数将导致选择的不等概及最终样本中的代表性不成比例。为了修正选择的偏倚，加权是必不可少的。

不成比例的分层好处在于增加某一有较高的标准差的层的抽样数，而使该层的抽样变异有所降低。理解这一做法为什么能降低变差这一点，将对理解和掌握标准差的计算公式不无帮助。

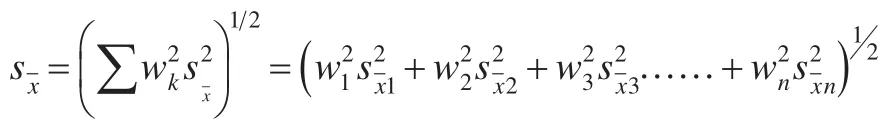
除了每一层的标准差已经计算出来之外，这一公式都与上面介绍的比例分层的公式相同。这两个公式的任何一个，既可用于比例分层，也可以用于不成比例的分层。

首先计算每层的标准差，然后再把它们合并成一个加权平均数，所以标准差最大和权数最大的层对标准差的影响最大。用不成比例的分层增加具有最大的抽样误差的层的层内样本量，将会降低该层的抽样误差，从而使整个样本的抽样误差也有所降低。表5用不成比例分层对这一性质做了阐述。该表的分层与表2～表4中的例子相同。用设计效应的平方根这一指标，测得抽样误差降低了将近2%，每一种不成比例的分层的抽样误差都小于对应的每一种比例分层抽样误差。例如按母亲教育程度分层的高效单元分配的标准误差为3.48，而以同一变量作比例分层的则为3.56。前者略低于后者，并不是特别显著。

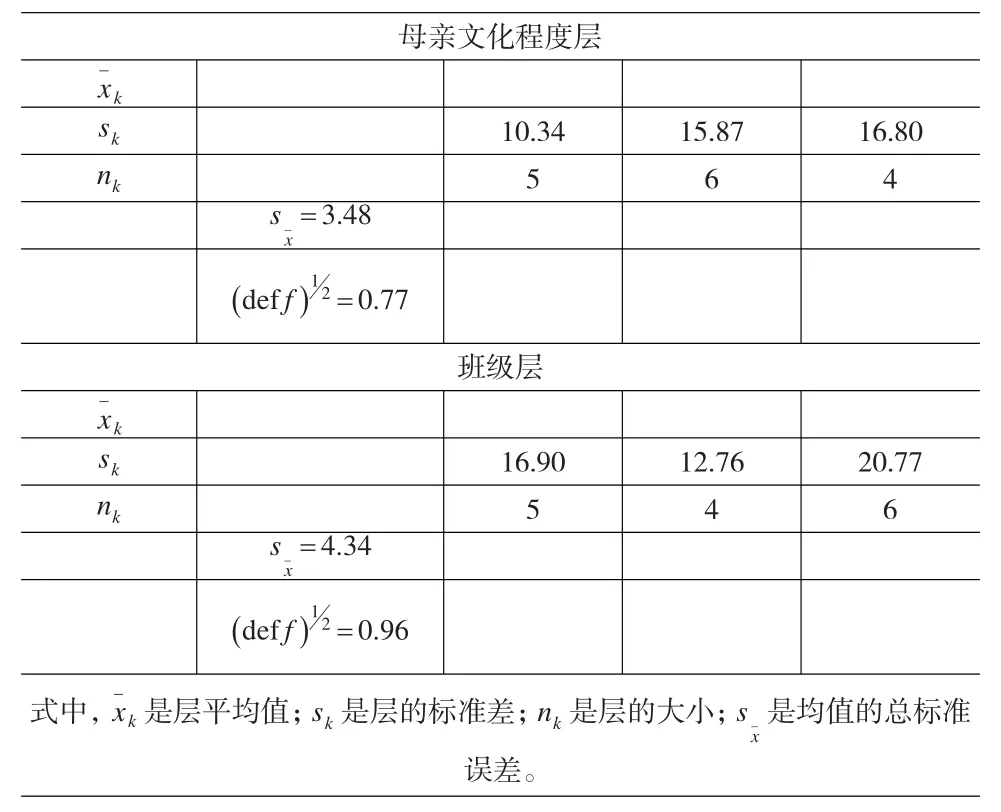
表5 分层样本量高效分配：层样本量变动的结果

为了最大限度地提高总体估计值的精确度，样本量应与标准差和层的大小成比例：

式中，nk是层的样本量；n是总样本量；Nk是总体的层的样本量；Sk是层的标准差。

虽然这一公式看起来似乎是合乎逻辑的，但实际上总体和层的标准差几乎都是未知的。所以，分配给每一层的抽样单元不是那么精确，

但是在标准差，或在更多的时候是它们的相对大小可以以被估计的时候，对层的抽样单位数进行分配将会使估计值的精确度有所提高。在表4所列的两个例子中，对第一个例子中的15个抽样单位中的2个做了重新分配，对第二个例子中的一个抽样单位作了重新分配。在第一个例子中，我们将A1层中的抽样单位减少2个，给A2和A3分别增加了1个。在第二个例子中，我们从B2层中取走了一个抽样单位，加到了B3层。可以用与估计高效样本量的标准差相同的方法来估计每一层的变差。

4 总结

比例分层抽样的优点在于能提高估计值的精度和确保分层的群体的比例的代表性。分层本身并不需要什么额外的费用。但研究总体的每一成员都必须列出，并按用于分层的变量分类。而要得到有关整个总体的诸如这样的信息的费用则可能十分昂贵。有时得到与我们期望的分层的变量有关的信息的费用则可能不那么昂贵。例如，从成本效益的角度看，收集有关整个学生总体母亲文化程度的信息可能得不偿失。但是我们却有学生居住的地区的信息，可作为社会经济地位的信息的指标加以利用，而这一指标可能与母亲的文化程度相关。

如有需要对子群体进行分析，而按比例选取产生的子样本的标准差又过于大的时候，要采用不成比例分层抽样。这时不成比例的分层抽样使我们得以在不必成比例地加大总样本量的前提下，加大子总体的样本量。要能这样做，我们要以能使子总体的成员与这一特定层次联系在一起的方式来定义这个层。实现这一目的的理想分层都发生在层是由互斥的子总体的成员组成的时候。在子总体的成员是高度集中的时，不成比例抽样也同样可以使用。

不成比例分层的主要缺点是在计算标准差的时候必须要加权。这样标准差的计算势必会更加复杂。此外，保存的数据集中不仅必须有专门用来识别层的编码，还必须包括分层赖以生成的权数。许多统计软件都有用于设置总体估计值和标准差计算的权数的程序或命令。抽样中最为常见的错误是在样本选择时采用的是不成比例的抽样，但却在估计过程中没有加权，因而未能对总体估计值中的这一偏倚进行修正。

[1]加里·T.亨利著.实用抽样方法[M].重庆：重庆大学出版社,2008.

[2]刘爱琴，吴玉香.分层抽样中样本量的分配方法研究[J].山东财政学院学报，2007（04）

[3]刘红英.关于多目标分层抽样方法及其应用研究[D].西安：西安财政学院，2010

[4]范雯雯.利用蒙特卡罗方法模拟期权价格的实证分析——基于方差减缩技术中的分层抽样方法[J].时代金融，2013，（5）.

[5]邱赛兵，唐波.分层抽样下多项选择敏感问题随机抽样调查方法及应用[J].湖南人文科技学院学报，2013，（2）.

[6]戴林送，林金官.广义泊松回归模型的统计诊断[J].统计与决策，2013,（11）.

[7]王战伟.非线性数据拟合的递推法及程序实现[J].统计与决策，2013,（12）.

[8]周庆元.PPS和简单随机抽样估计效率的实证检验[J].统计与决策，2014,（1）.

[9]郝枫.价格体系对中国要素收入分配影响研究——基于三角分配模型之政策模拟[J].经济学（季刊），2013，（10）.

[10]魏志华，林亚清等.家族企业研究:一个文献计量分析[J].经济学（季刊），2014，（1）.

[11]朱胜，刘锦扬，成美纯.当前抽样调查工作存在的几个问题及解决途径[J]，经济学（季刊），2014，（1）.