一种自适应的混沌粒子群优化RBF神经网络算法

张 义，田爱奎，韩士元

(1.山东理工大学计算机科学与技术学院，山东淄博 255049; 2.济南大学信息科学与工程学院，济南 250022)

一种自适应的混沌粒子群优化RBF神经网络算法

张 义1，田爱奎1，韩士元2

(1.山东理工大学计算机科学与技术学院，山东淄博 255049; 2.济南大学信息科学与工程学院，济南 250022)

为了提高RBF神经网络的预测效果，针对RBF神经网络的不足提出一种自适应混沌粒子群优化RBF神经网络算法(SACPSO-RBF)。该算法主要采用自适应和混沌操作，采用粒子群算法对RBF神经网络进行优化。利用个体的变异、个体之间的交叉操作和个体的混沌扰动，有效克服了粒子群算法的局部收敛性。使用该优化算法对测试函数序列进行预测，并对算法的有效性进行检验。实验结果表明:改进的算法具有良好的预测能力。

混沌;自适应;RBF神经网络;变异;交叉

径向基函数神经网络(RBFNN)是由输入层、隐含层和输出层构成的一种特殊的3层前馈神经网络，具有结构简单、非线性逼近能力强、收敛速度快以及可全局收敛等优点［1］。尽管该网络有诸多优点，但是其网络结构设计参数(包括隐含层节点个数、中心、宽度和隐含层与输出层的权值等)难以确定。粒子群算法(PSO)是一种群体优化算法，具有良好的全局寻优特点。因此，将这两种算法相结合，对PSO算法中的粒子结构使用RBF的参数设定，通过PSO算法寻找最优参数，从而为RBF设定最优的网络结构。

尽管PSO算法具有可全局寻优的特点，但是PSO算法会陷入“早熟”，寻优效果不是很理想［2］。针对以上不足，本文提出一种自适应的混沌粒子群优化RBF神经网络的算法［3-19］。针对PSO的“早熟”现象，使用混沌扰动的方法对全局最优粒子进行干扰，以跳出局部最优。通过模拟退火算法，使用自适应交叉变异的方法增加粒子的多样性，提高PSO算法的全局搜索能力。

1 自适应混沌粒子群优化RBF神经网络算法

1.1 RBF神经网络

RBF神经网络是3层前馈网络，主要包括输入层、隐含层、输出层。假设在D维空间内有M个样本，则第i个样本的为输入向量，i∈［1，M］。N为输出解空间维度，令Y= (y1，y2，…，yn)为输出向量。使用高斯函数作为隐含层的径向基函数，公式如下:

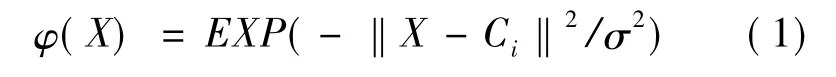
神经网络的输出公式为

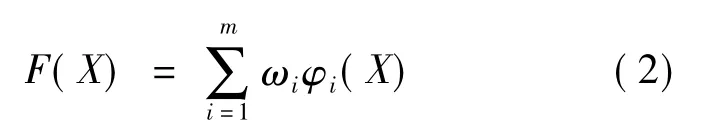
其中:ωi为隐含层中第i个结点到输出结点的权值;m为隐含层结点的个数。

1.2 粒子群优化算法

粒子群算法因模拟鸟群捕食行为而得名，是众多集群智能算法中的一种，具有快速搜索能力和全局寻优功能［3］。

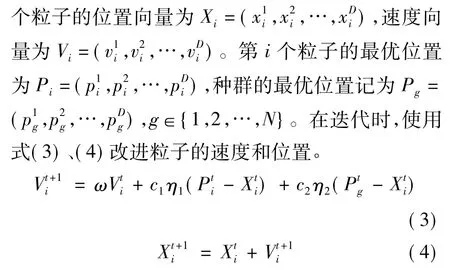
其中:ω为惯性权重;c1，c2为加速度系数;η1，η2

为［0，1］的随机数。

1．3 优化工作

1．3．1 混沌

利用Logistic混沌序列扰动粒子群，其步骤如下:

1)将初始粒子根据式(5)映射到［0，1］范围内，当xi∈［ai，bi］时，公式为

2)根据Logistic公式生成序列:

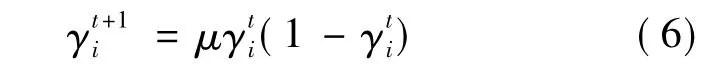
当μ接近4时，Logistic处于混沌状态。可以使用该公式得到N个混沌的解空间。

3)将步骤2)中生成的混沌空间中的向量根据式(7)映射到原始解空间范围内，得到向量组X={X1，X2，…，Xn}，公式如下:

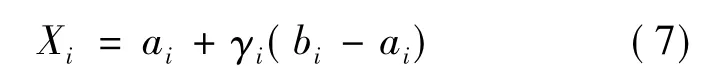
1．3．2 变异

对粒子采取变异操作，将粒子Xi根据式(8)进行变异。如果新产生的粒子适应度优于原始粒子，则使用新粒子替换原始粒子。

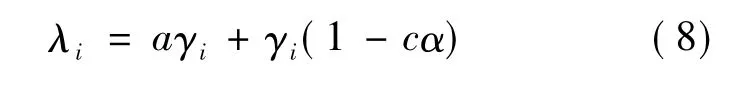
其中:α［0，1］表示条件系数;c为抗体的浓度，是适应度最大的粒子个数与粒子总数的比值。

1．3．3 交叉

粒子在迭代更新过程中，使自身粒子与其他粒子相交叉，生成相同数目的子粒子。若子粒子的适应度有所改进，则替换原来的粒子以增加粒子群粒子的多样性。交叉公式如下［6］:速度交叉公式为:

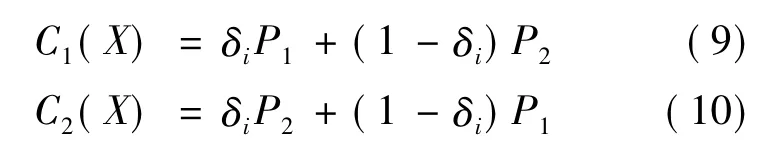
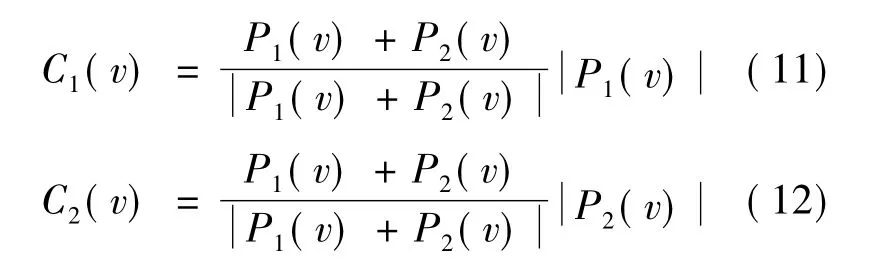
式(9)～(12)中:δi∈［0，1］;Ck(X)为子粒子的位置;Ck(v)为子粒子的速度。

1．3．4 自适应

在PSO算法中，当参数ω较大时，利于全局搜索;当ω取值较小时，局部搜索能力强，利于获取最优精度解。因此，本文使用自适应的ω，c1，c2取值方式，即在开始时采用较大的系数，使粒子以较快的速度接近最优粒子;在完成一定程度的搜索后，使用较小的系数，提高群体局部搜索的能力，查找最优解。公式如下:

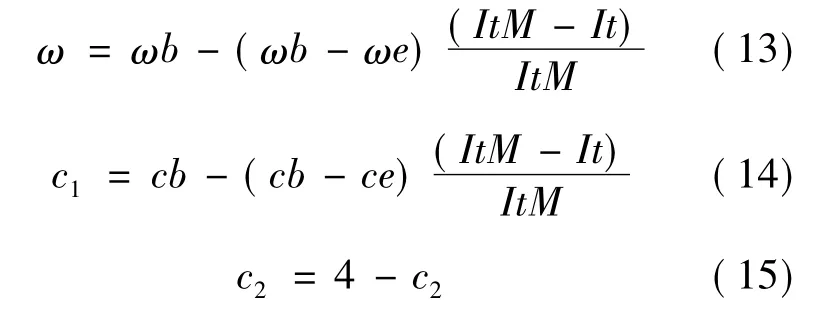
其中:0．1≤ωe≤ωb≤0．9;0＜ce≤cb≤4;ItM是最大迭代次数;It是当前迭代次数。

1.4 算法优化

自适应混沌粒子群优化RBF神经网络算法流程如图1所示，其中粒子寻优部分的流程见图2。

步骤1 粒子群初始化

采用2级结构粒子。第1级采用二进制编码，使用0/1表示隐含层节点所处状态，0是休眠，1是激活;第2级采用十进制编码，每位代表RBF神经网络的相关参数(中心点、宽度)，结构如图3所示。

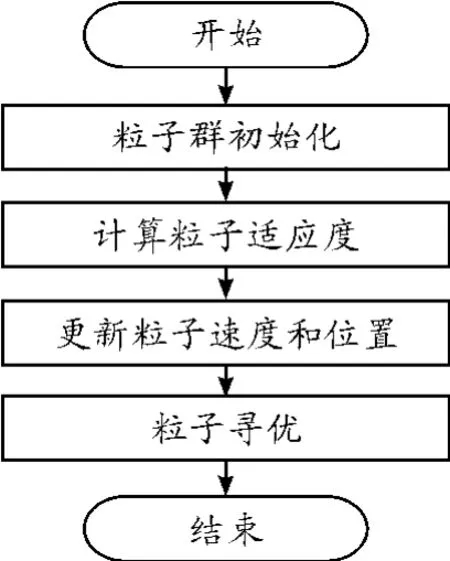
图1 自适应混沌粒子群优化RBF神经网络算法流程

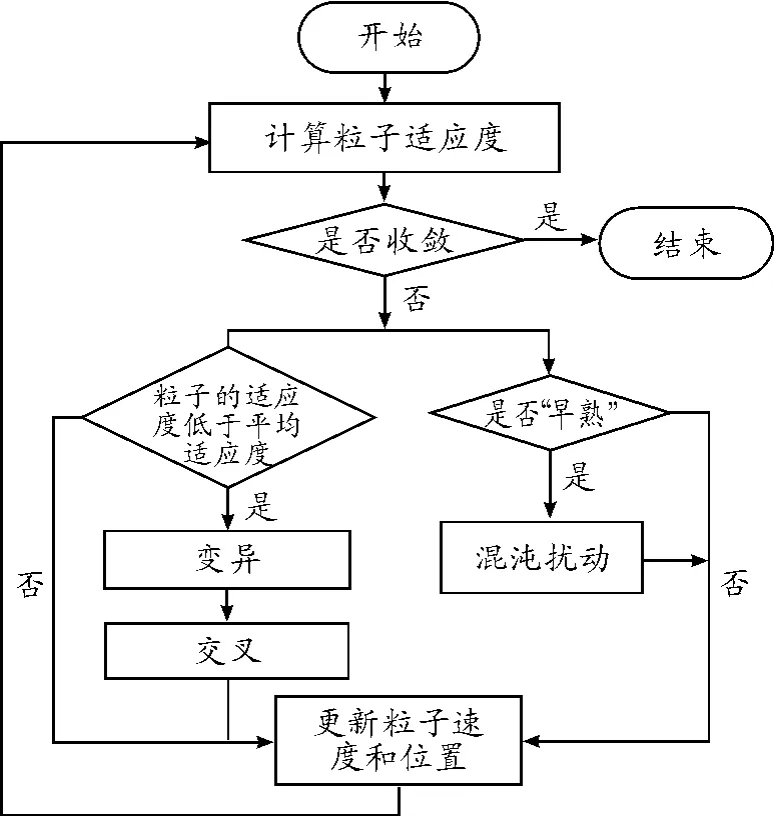
图2 粒子寻优流程

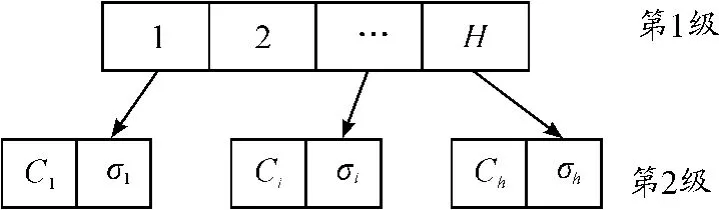
图3 粒子结构

隐含层节点的个数可以根据式(16)确定［2］:

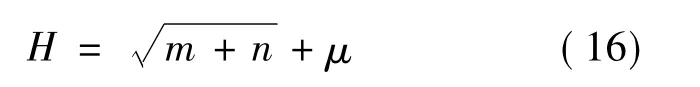
其中:μ∈［1，10］;m为输入节点个数;n为输出节点个数。因此，设置第1级编码中的基因个数为H。随机选取H个样本Xi为初始化中心Ci，初始化宽度σi根据式(17)计算获得，i=1，2，…，H。

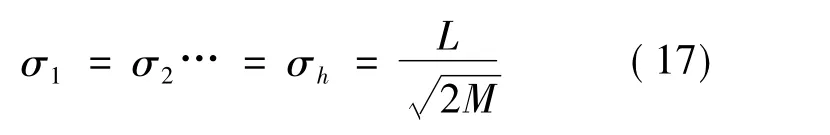
其中:L为选取中心的最大距离;M为隐含层结点个数。使用LMS方法获取计算权值ωi。

步骤2 根据式(18)计算每个粒子的适应度值。

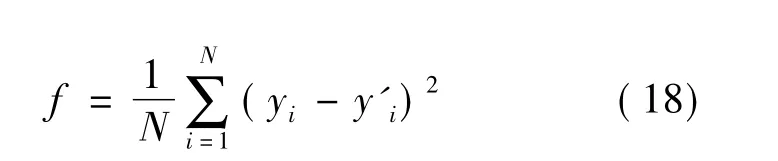
其中:N为粒子总数;yi为输出结点的目标输出值;y'i为实际的输出值。

步骤3 根据式(3)、(4)更新粒子位置速度，取得新一代的粒子群。ω，c1，c2采用式(13)～(15)进行更新。

步骤4 粒子干扰并寻优的过程如下:

1)计算新一代粒子群的适应度值，判断是否满足条件，若满足，转向步骤6);否则转向步骤2)。

2)根据式(18)～(20)计算群体适应度方差σ2:

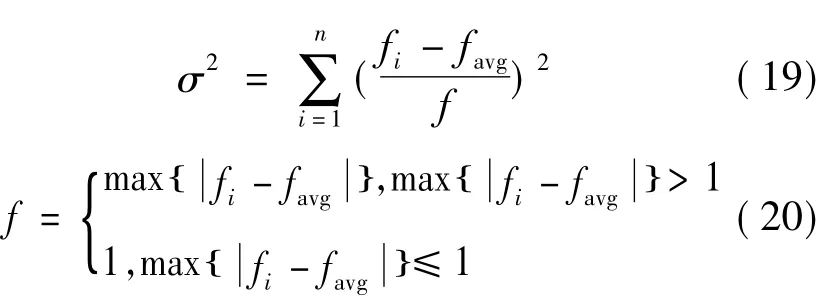
其中:fi代表第i个粒子的适应度值;favg为粒子群中所有粒子的平均适应度。σ2能够表现种群的搜索收敛情况，其值越小越收敛。若前后两次σ2的差小于某个很小的阈值，可以认为搜索过程中出现了“早熟”现象。若搜索出现“早熟”现象，则对粒子群最优位置向量进行混沌扰动，并计算混沌扰动后的向量获取最优的粒子P*。用P*向量随机取代群体中的某个粒子，从而增加粒子群的多样性，跳出局部最优的限制。

3)若粒子P的适应度小于平均适应度，则根据式(8)对粒子进行变异，并根据新粒子的适应度优劣替代原粒子。

4)若粒子P的适应度小于平均适应度，则根据式(9)～(12)对粒子进行交叉，并根据新粒子的适应度好坏替代原粒子。

5)更新粒子位置速度，返回步骤1)。

6)进化结束，返回最优解。

2 仿真结果分析

本文采用测试函数——Schwefel函数进行仿真分析，其函数公式为

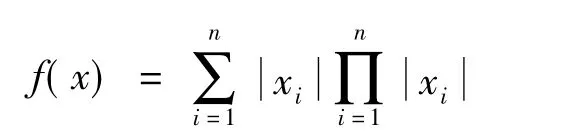
使用该函数产生100个样本数据，前80个样本作为培训样本，后20个样本用于模型测试。本文将SACPSO-RBF算法与RBF算法的结果进行比较。图4为SACPSO-RBF与RBF两种算法针对每个测试样本的预测值与函数真实值的对比情况。图5是两种算法针对每个测试样本的误差对比。对比结果表明:在相同维度、相同的测试数据情况下，SACPSO-RBF算法比RBF算法拥有更好的预测精度。表1为相同测试数据下，在不同维度中两种算法的误差绝对值总和的对比。从表1中可以看出:随着维度的增大，SACPSO-RBF算法相比RBF算法拥有更明显的优势。

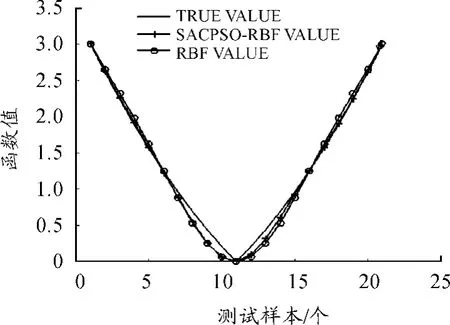
图4 预测值与真实值对比

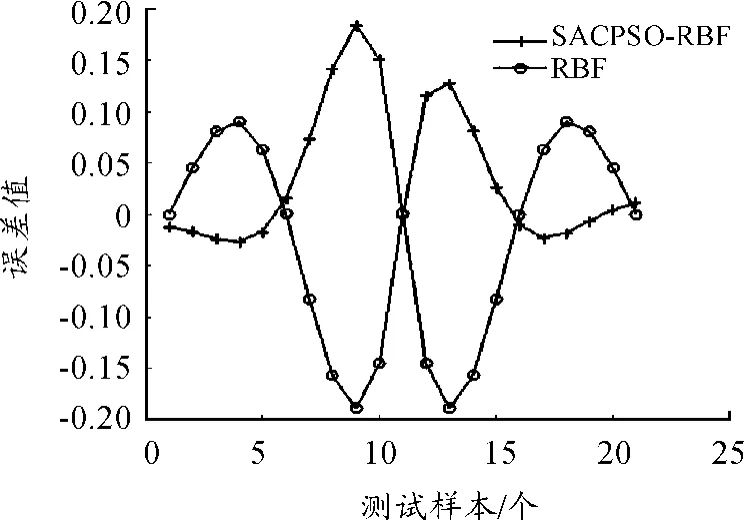
图5 误差对比

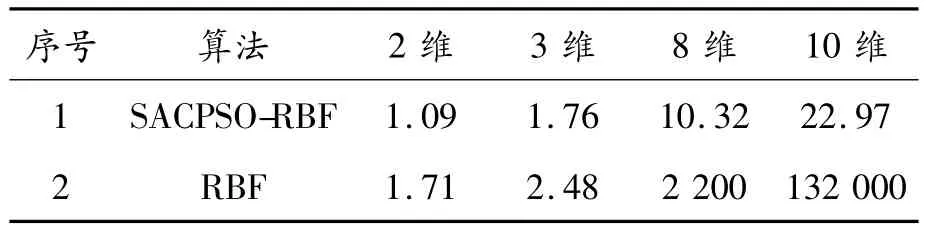
表1 总误差对比

3 结束语

通过使用自适应的混沌粒子算法对RBF神经网络进行优化，使得RBF神经网络结构得到最优化。使用混沌扰动和自适应算法对PSO算法进行优化，克服了PSO易陷入“早熟”的缺点。最后，通过仿真分析验证了优化工作的有效性。

参考文献:

［1］郝晓丽，张靖.基于改进自适应聚类算法的RBF神经网络分类器设计与实现［J］.计算机科学，2014，41 (6):260-263.

［2］孟萌萌.基于RBF神经网络短期热网负荷预测研究［D］.哈尔滨:哈尔滨工业大学，2013.

［3］王亚，熊焰，龚旭东，等.基于混沌PSO算法优化RBF网络入侵检测模型［J］.计算机工程与应用，2013，49 (10):84-87.

［4］王博.基于线性回归和神经网络的预测模型在国民经济数据中的应用［D］.长春:吉林大学，2012.

［5］王芹芹.基于主成分分析和RBF神经网络的融雪期积雪深度模拟［J］.干旱区资源与环境，2014，28(2): 175-178.

［6］李雪.基于粒子群的粮食产量预测神经网络优化研究［D］.舟山:浙江海洋学院，2014.

［7］王晓军.神经网络建模方法及数据挖掘在煤造气过程中的应用［D］.北京:北京交通大学，2014.

［8］张方舟，郝庆辉，周勃，等.遗传算法的RBF神经网络在线损计算中的应用［J］.计算机技术与发展，2014，24(6):192-195.

［9］刘洁，李目，周少武.一种混沌混合粒子群优化RBF神经网络算法［J］.计算机技术与发展，2013，23(8): 181-184.

［10］朱玉，赵卿，周兴东.基于混沌免疫优化RBF网络的遥感水深反演［J］.计算机工程，2013，39(5):188 -191.

［11］武燕.粒子群改进算法及在混合神经网络中的应用研究［D］.景德镇:景德镇陶瓷学院，2014.

［12］李艳玲.基于神经网络的电力系统负荷预测问题研究［D］.沈阳:沈阳工业大学，2014.

［13］葛珉昊.基于混合递阶遗传算法的RBF网络优化及在BOD软测量中的应用［D］.兰州:兰州工业大学，2014.

［14］陈伟淳.基于多神经网络的智能电网短期负荷预测研究［D］.广州:华南理工大学，2012.

［15］曹秋燕.基于SVM和PSO的信用评级模型研究［D］.杭州:浙江工商大学，2013.

［16］方一新.改进BP神经网络的EMG手指运动识别［J］.激光杂志，2014(9):92-95.

［17］兰胜坤.遗传算法优化BP神经网络的说话人识别系统［J］.重庆理工大学学报:自然科学版，2013(10):91 -95.

［18］彭继慎，程英.优化RBF神经网络在压力传感器中的应用［J］.压电与声光，2012(3):414-416.

［19］钟宇平.基于神经网络及强化学习的智能控制系统［J］.西南大学学报:自然科学版，2013(11):172 -179.

(责任编辑杨黎丽)

An Adaptive Chaotic Particle Swarm RBF Neural Network Optimization Algorithm

ZHANG Yi1，TIAN Ai-kui1，HAN Shi-yuan2
(1.College of Computer Science and Technology，Shandong University of Technology，Zibo 255049，China; 2.School of Information Science and Engineering，University of Jinan，Jinan 250022，China)

In order to improve the prediction results of RBF neural network，this paper proposed an adaptive chaos particle swarm optimization algorithm of RBF neural network(SACPSO-RBF)according to the shortcomings of the RBF neural network.This algorithm mainly used the adaptive chaotic particle swarm optimization algorithm to optimize the RBF neural network.The use of variation between individuals，the cross over operation and individual chaos disturbance can effectively avoid the local convergence of the particle swarm optimization algorithm.Using the optimization algorithm，we predicted the testing function sequence and tested the validity of the algorithm.Finally，the experimental results show that the algorithm has well prediction ability.

chaos;adaptive;RBF neural network;variation;cross

TP301.6

A

1674-8425(2015)11-0126-05

10.3969/j.issn.1674-8425(z).2015.11.021

2015-04-22

山东省优秀中青年科学家科研奖励基金资助项目(BS2014DX015)

张义(1983—)，女，山东人，硕士研究生，主要从事计算机信息化研究;田爱奎，男，山东人，博士，主要从事计算机教育游戏研究。

张义，田爱奎，韩士元.一种自适应的混沌粒子群优化RBF神经网络算法［J］.重庆理工大学学报:自然科学版，2015(11):126-130.

format:ZHANG Yi，TIAN Ai-kui，HAN Shi-yuan.An Adaptive Chaotic Particle Swarm RBF Neural Network Optimization Algorithm［J］.Journal of Chongqing University of Technology:Natural Science，2015(11):126 -130.