基于COMSOL声表面波扭矩传感器的有限元分析

李志鹏，李晓英，邵宪友

(东北林业大学交通学院，哈尔滨 150040)

基于COMSOL声表面波扭矩传感器的有限元分析

李志鹏，李晓英，邵宪友

(东北林业大学交通学院，哈尔滨 150040)

基于对汽车转向扭矩测量方法的研究，重点分析了SAW扭矩传感器的工作机理以及优势，并建立其力学和数学模型。分析了作为转向扭矩传感器的核心元件弹性轴以及压电膜片的选择要素，并基于COMSOL的大型仿真功能对弹性轴和压电膜片进行有限元分析，模拟了声表面波扭矩传感器的力学特性，保证了敏感膜片以及弹性体在承受最大扭矩时不至于破坏，在承受最小扭矩时能够保证其灵敏度，为汽车转向SAW扭矩传感器的器件设计提供理论依据。

转向扭矩;COMSOL;压电膜片;弹性轴;有限元分析;灵敏度

电动助力转向系统EPS已成为助力转向系统的一大发展趋势［1］，其主要组成部分为机械转向系统、转向扭矩传感器、控制器等。转向扭矩传感器对助力系统有重要的影响，也成为汽车研究中的热点。针对汽车转向扭矩传感器，基于声表面波传播理论［2-3］和应变片工作原理［4］，应用COMSOL软件的物理仿真功能对弹性轴和压电膜片进行有限元分析，模拟出汽车转向SAW扭矩传感器件的力学特性，保证器件能够满足汽车转向扭矩测量中的实际需要，即当承受最大扭矩时器件不会受到破坏，当承受最小扭矩时器件能够较准确地测出输入扭矩。对压电模块进行一系列仿真实验。结果表明:选取的铌酸锂晶体能够较好地满足SAW扭矩传感器件的力学性能要求。用Matlab对在承受最大扭矩时的材料表面的应力进行统计分析，其结果为双通道SAW扭矩传感器的叉指换能器位置的设计提供了依据，为实现汽车转向节能化提供参考。

1 转向扭矩测量方法及传感器

1.1 常用转向扭矩测量方法及传感器

扭矩测量是将电子、机械等多种物理场结合在一起的技术。扭矩测量的三大关键分别是能量供给、传感准确度、高效传输［2］，其中传感准确度是传感器研究的主要问题之一，对传感器整体起着决定性作用。目前，国内外扭矩测量方法主要有应变型、磁弹性型、转角型［5］。应变型传感器因具有测量精确度高、结构简单、操作简便以及其量程范围基本上可满足所有需求等特点，被广泛应用于静态或低速旋转系统的测量。根据旋转体上的桥压输入和测得的应变信号输出的采集和处理方法的不同，相应地分为传统集流环式、数字式［6］。

1)集流环式

集流环式采用导电滑环来传递扭矩。导电滑环属于摩擦接触，容易使器件受损并且产生热量，影响实验结果的准确性，造成不必要的能量损失，降低材料的使用寿命。同时，器件工作时产生很大的噪声，造成噪声污染。

2)数字式

根据实验中被测对象以及其测量范围，在特定的弹性轴上贴上应变片，组成相应的电桥，确定基础转矩测量传感器。

传统的电阻式扭矩传感器根据弹性轴在受到外界输入扭矩时发生形变，电阻应变片的电阻随之呈线性变化的原理，通过对应变片电阻的测量实现对转向扭矩的测量。但是电阻式扭矩传感器当轴体产生较大应变时有较大的非线性特性，并且输出信号较弱。

本文研究的是新型SAW扭矩传感器。SAW扭矩传感器利用叉指换能器(IDT)在压电基体直接激励和接受声表面波。声表面波是指在弹性体自由表面产生并沿着表面或界面传播的各种模式的波，在大多数固体中的传播速度为2～10 km/s，在数量级上比电磁波低4～5个数量级，85%的能量是沿着固体表面传播出去的。因此，在压电基体表面上制备叉指换能器能够非常方便地传播和截取声表面波信号，从而实现滤波、延时、传感等功能。声表面波在压电基体上的传播过程如图1 (a)所示，叉指换能器结构如图1(b)所示。IDT的电极间距和电极宽度分别记为a和b，当二者相等时，叉指周期为均匀周期，叉指换能器的相邻电极构成电极对。因此，叉指周期T=2×(a+b)，其重合的电极长度为有效指长，也称为换能器的孔径，记为w。

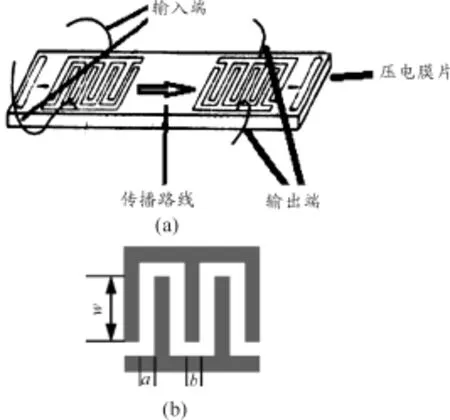
图1 SAW传播过程及IDT构造

1.2 转向SAW扭矩传感器的优点

转向SAW扭矩传感器的优点包括以下几个方面［3］:①信号处理简单、方便;②器件适用于批量生产;③使用时性能稳定且表现出优异的可替代性，可重复性好;④ 随着电子以及机械技术的不断改进，SAW器件会不断地进行更新，体积、质量以及功耗都将会慢慢降低，而精度和灵敏度会有相应的提高，同时能够在高温等较为恶劣的环境下工作;⑤易实现无线化。

2 转向SAW扭矩传感器的设计

2.1 理论依据

如图2(a)所示，用相邻的2个截面p和q从转轴上截取长度为dx的微体。假定在转轴上施加一定的扭矩，转轴发生一定的变形，扭转角记为φ。扭矩剪应力分布如图2(b)所示。

根据材料力学相关理论［7］，剪应力在横截面上的分布公式为:

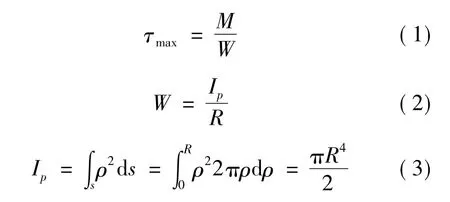
其中:τmax为轴面上最大剪应力;W为轴截面系数;Ip为横截面对圆心的极惯性矩;ρ为横截面上任一点到圆心的半径;R为转轴半径。

综上，最大剪应力与扭矩之间的关系为

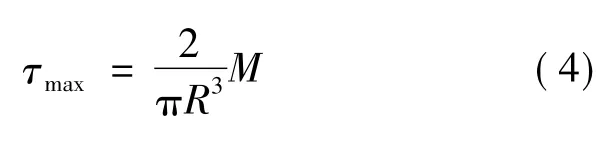
取单元体A进行应力分析，如图2(c)所示。由切应力互等定理可知:单元体4个侧面受力大小相等，处于纯剪切状态。同样，对单元体A进行平面二向力状态分析，假定斜截面的面积为dA，与y轴夹角为α，根据法向力和切向力平衡，可知转轴上任意横截面所受应力为:

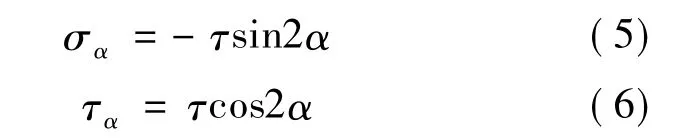
因此，当α=±45°时，正应力σa=±τmax，而切应力τq为0。所以，应变片应沿轴向45°和轴向135°进行粘贴，此处位置只受到最大的拉应力和压应力。

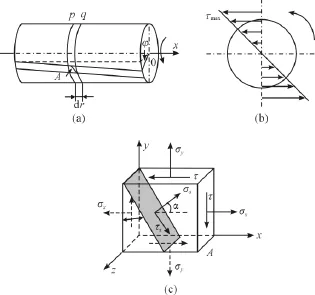
图2 转向轴力学理论分析

2.2 弹性体设计

汽车转向轴传递驾驶员对方向盘的输入扭矩，也是应变片式扭矩传感器的关键组成部分。轴体材料的选择影响着传感器的整体性能，本文弹性轴使用的材料为弹性钢。弹性钢是指在淬火和回火状态下具有良好弹性的钢材，在规定的载荷下，弹性变形的能力使其承受一定的载荷，在载荷去除后，不产生永久变形，具有优越的力学性能和冶金质量，并且具有良好的表面质量。弹性钢的力学性能和化学成分［5］见表1和表2。

表1 弹性钢力学性能

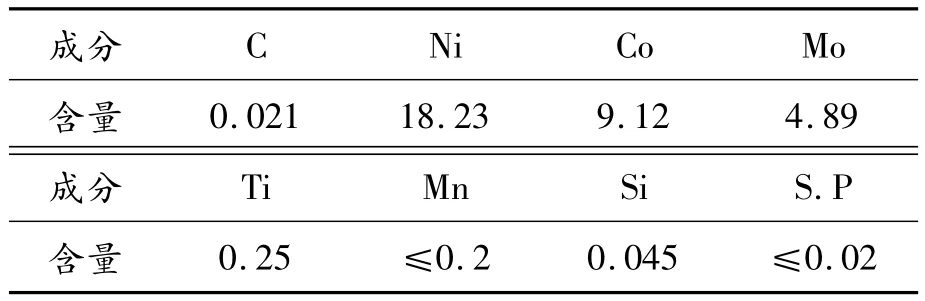
表2 弹性钢基本化学成分

根据汽车转向轴的最大输入扭矩M=100 N/m以及理论力学的相关计算，选定轴体直径D= 20 mm，能满足在大扭矩的输入下轴体的刚度以及屈服极限的要求，也能确保在扭矩较小的输入下提供足够的弹性应变。

2.3 压电基片

压电材料是指受到压力作用后在其两端面会出现电荷的一大类单晶或多晶的固体材料［8-12］，它是声表面波器件进行能量转换和信号传递的重要载体［2］。目前，使用最为广泛的压电材料包括压电单晶(如石英、铌酸锂等)、压电陶瓷(如锆钛酸铅陶瓷等)和压电薄膜(如氧化锌薄膜、氮化铝薄膜、铌酸锂薄膜等)这三大类。压电材料种类很多，各有优缺点，对其的一般要求［3］如下:

1)具有良好的表面，表面粗糙度尽可能小，方便制备高性能的叉指换能器;

2)具有较小的传播损耗，一般在0.2 dB/λ;

3)具有较高的机电耦合系数K2，其数值在0.5%以上;

4)材料成本较低且便于批量化生产。

本文选取石英单晶、铌酸锂单晶和氧化锌薄膜作为压电基片，分别建模进行有限元分析，模拟出各自的力学特性。为了不破坏轴体尺寸，选定3个膜片的平面尺寸均为50 μm×50 μm，高度为30 μm。

3 转向轴及压电膜片模型的建立

器件仿真工作是器件设计和制作的基础，通过仿真可以有效提高设计效率，同时能减少材料的使用，防止造成不必要的浪费。目前，大型有限元分析软件主要有ANSYS、ANSOFT、COMSOL，可以利用这些软件对SAW扭矩传感器进行仿真分析。相比ANSYS、ANSOFT等软件，COMSOL软件具有完全开放的架构，有专业的计算模型库，用户可以自己定义所需要的仿真分析方程，并根据自己的仿真需要选择相应的物理模型进行一定的修改。同时，COMSOL软件的后处理功能非常强大，可以进行各种数据、曲线、图片及动画的输出与分析。

3.1 转向轴三维模型的建立

打开COMSOL软件，选择三维空间，物理场选定为固体力学。本文对轴体进行仿真分析是为了求解轴体在静态载荷作用下的变形、应力和应变，因此轴体分析的物理场接口的预置求解为稳态研究。在几何窗口新建工作面，选择添加圆柱体，在输入窗口分别输入相应的直径和轴长，点击全部构建，圆柱体模型即初步建立。然后进行模型边界条件的设定，分别点击圆柱体上、下表面，其中一面的边界条件为固定，另一面则为载荷边界条件，用以施加载荷。本文轴体采用弹性钢，在仿真软件中选择结构钢即可满足分析要求。网格划分的序列类型为物理场控制网格，单元格类型为细化。建立的初步仿真模型如图3所示。

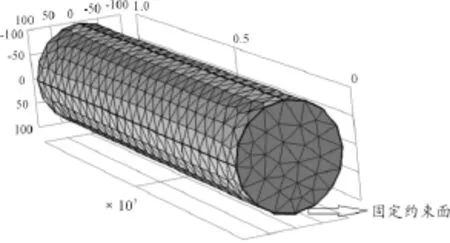
图3 转向轴仿真模型

3.2 压电膜片三维模型的建立

石英单晶、铌酸锂单晶和氧化锌晶体的特性参数［2］如表3所示。同时，将膜片的压电、弹性、介电常数分别输入到COMSOL软件材料属性框中，将压电膜片的高宽以及厚度输入到模型中。边界条件设定如图4所示，上表面为自由边界条件，下表面为固定边界条件，其余4个面均设定为边界载荷条件。

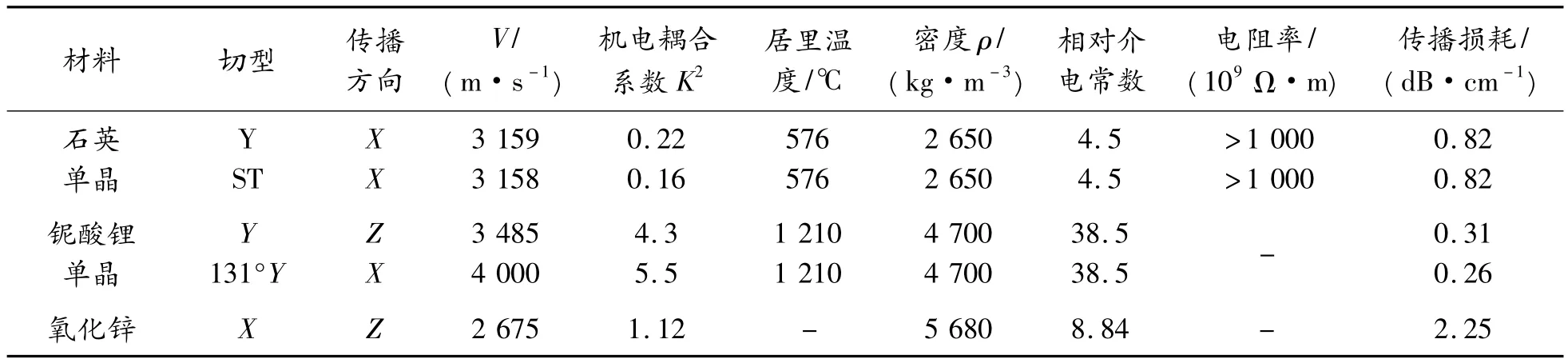
表3 压电材料的特性参数

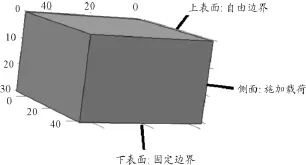
图4 压电膜片仿真模型边界条件

4 转向轴及膜片的仿真分析

4.1 转向轴仿真分析

本文转向轴直径D=20 mm，轴长L= 100 mm，将M=100 N·m输入到边界条件中后点击计算模块对模型进行仿真。转向轴变形后的应力分布如图5所示。

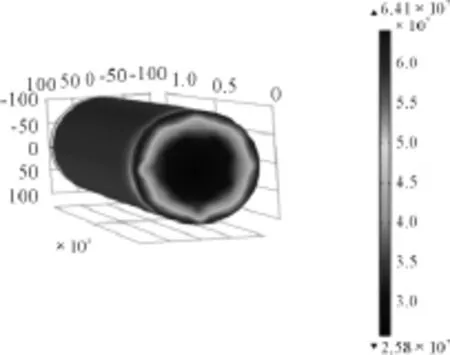
图5 在转向轴施加扭矩M=100 N·m时的应力分布

在同一个截面内，圆轴表面具有最大的切应力τ'=6.41×107Pa，与理论值基本一致，并且从图5中可以看出:轴表面剪应力分布均匀、无应力集中及梯度变化现象，为SAW扭矩传感的稳定性提供了前提［13-21］。

4.2 压电基片仿真分析

当压电膜片与轴呈±45°放置时，侧面受到的压应力即为轴体最大表面切应力。根据轴体的仿真分析可知:轴体在受到最大输入扭矩时，最大切应力τ'=6.41×107Pa。分别将1=0，2=1.41× 107Pa，3=2.41×107Pa，4=3.41×107Pa，5= 4.41×107Pa，6=5.41×107Pa，7=6.41×107Pa输入到COSMOL边界载荷条件中，对石英单晶体、铌酸锂单晶体和氧化锌晶体3个模型做7组仿真实验，并读取其最大应力值。采用Matlab软件的数学分析功能对实验数据进行统计分析。分析结果如图6所示。从图中可以看出:压电膜片的应力与输入剪应力呈线性变化。由式(3)和(4)可知:压电膜片应力与被测扭矩呈线性关系，即压电膜片的应变与扭矩加载呈线性关系，因此被测扭矩可以通过测量压电膜片的应变得到。初步仿真结果表明:选择石英单晶体、铌酸锂单晶体和氧化锌晶体作为应变片来测量扭矩是可行的。从图6也可见铌酸锂单晶体的应变性能最好。因此，选用铌酸锂单晶体作为SAW式扭矩传感器的应变片。

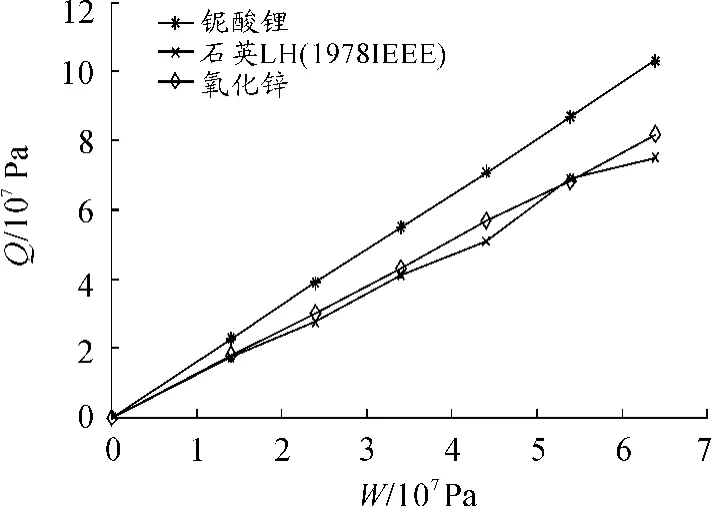
图6 压电膜片承受压力时膜片最大应力曲线

图7 压电膜片表面应力分析

正方形铌酸锂膜片沿Z轴方向的应力分布如图8所示。从图中可以看出:COSMOL软件将正方形铌酸锂膜片沿着X方向分为10份，应力分布等分12份，在X=25 μm处为应力分布的分界点，两侧压力都逐渐增大，保证了在现有的几何结构和相应的尺寸设计下压电膜片依然具有较高的敏感度。

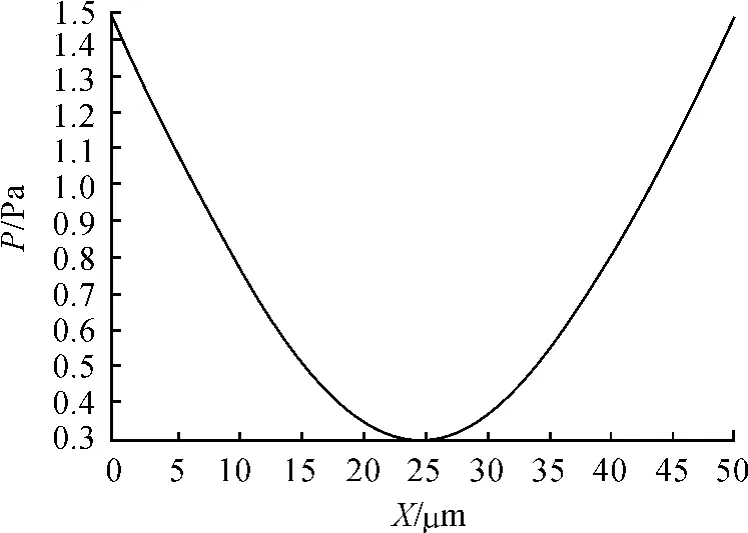
图8 铌酸锂膜片应力分布曲线

5 结论

1)轴体在受载后，轴表面剪应力分布均匀，无应力集中及梯度变化现象;

2)采用3种晶体作为压电膜片材料时，膜片表面应力与输入剪应力基本上呈线性变化，并且压电膜片应力与被测扭矩呈线性关系，即压电膜片的应变与扭矩加载呈线性关系;

3)相比石英单晶体、氧化锌膜片，铌酸锂单晶体的应变性能最好，因此选用铌酸锂单晶体作为SAW式扭矩传感器的应变片;

4)应力分布分为12个区域，从原点(铌酸锂膜片的中心)开始，应力逐渐增大，在膜片的边缘处达到最大值;

5)在X=25 μm处为应力分布的分界点，两侧压力都逐渐增大，较好地保证了压电膜片对被测量输入扭矩的敏感度。

［1］卢尚斌，孟广耀.电动助力转向系统中的转矩传感器设计［J］.机械设计与制造，2006(6):25-26.

［2］潘峰.声表面波材料与器件［M］.北京:科学出版社，2012.

［3］何鹏举，张朋，陈明，等.声表面波网络传感器及其在国防工业中的应用［M］.西安:西北工业大学出版社，2011.

［4］王岩，储江伟.扭矩测量方法现状及发展趋势［J］.林业机械与木工设备，2010(11):14-18.

［5］胡德福.应变式扭矩传感器的设计技术［J］.船舶工程，2011(4):96-99.

［6］卢尚斌，孟广耀.电动助力转向系统的转矩传感器设计［J］.机械设计与制造，2006(6):25-26.

［7］陈忠安，王静.材料力学［M］.北京:北京大学出版社，2009.

［8］李珉，柏逢明.双晶片压电材料微型驱动系统研究［J］.压电与声光，2014(6):929-932.

［9］冯莎莎，李方旭，肖定全.铌酸钾钠基无铅压电陶瓷的制备工艺技术研究进展［J］.功能材料，2014(19): 19001-19005.

［10］徐佩韦，张海波，肖建中，等.织构化钛酸铋钠基无铅压电陶瓷的制备与性能研究［J］.电子元件与材料，2014(7):8-11.

［11］赵兴强，温志渝.基于压电材料的振动能量收集器的谐振频率调节［J］.压电与声光，2013(2):241-244.

［12］李方旭，刘超，肖定全.钛酸铋钠基无铅压电陶瓷的组分设计与性能调控研究进展［J］.功能材料，2013(7): 913-917.

［13］水永安.声表面波与声表面波器件讲义［R］.南京:南京大学电子科学与技术系，2010.

［14］任姝.声表面波扭矩传感器结构设计及信号提取方法研究［D］.上海:上海交通大学，2013.

［15］徐继辉.应用于船舶传动轴扭矩检测的声表面波传感器设计［D］.上海:上海交通大学，2013.

［16］董辉平.声表面波传感器模拟与仿真［D］.太原:中北大学，2008.

［17］潘峰.声表面波材料与器件［M］.北京:科学出版社，2012.

［18］殷宝麟，于影，龙泽明，等.应变式扭矩传感器的设计研究［J］.机械设计与制造，2011(10):13-15.

［19］资新运，赵姝帆，耿帅，等.应变式扭矩传感器的分析及ANSYS仿真［J］.仪表技术，2014(10):50-54.

［20］Drafts B.Acoustic wave technology sensors［J］.IEEE Transactions on Microwave Theoy and Technology，2001，49(4):349-353.

［21］Krishnan R N，Nemade H B，Paily R.Simulation of One-Port SAW Rseonator using COSMOL Multiphysics［C］// Proceedings of the COSMOL Users Conference.Boston:［s.n.］，2006.

(责任编辑刘 舸)

Finite Element Analysis of Torque Sensor Based on COSMOL Surface Acoustic Wave

LI Zhi-peng，LI Xiao-ying，SHAO Xian-you
(Traffic College，Northeast Forestry University，Harbin 150040，China)

Based on the research of automotive steering torque measuring methods，we analyzed the work mechanism of SAW torque sensor and advantages，and established its mechanical and mathematical model.We analyzed selection elements of the elastic axis which is the core of steering torque sensor devices and piezoelectric diaphragm.Based on COMSOL’s large simulation function of elastic axis and piezoelectric diaphragm finite element analysis，we simulated the mechanics characteristic of the surface acoustic wave torque sensor，and ensured that the sensitive diaphragm and elastic under the maximum torque and cannot be damaged under the maximum torque and ensured its sensitivity when taking the minimal torque，which provides theoretical basis for designing SAW torque sensor for vehicle steering devices.

steering torque;COMSOL;piezoelectric diaphragm;elastic axis;finite element analysis;sensitivity

U463;TM571.2

A

1674-8425(2015)11-0017-06

10.3969/j.issn.1674-8425(z).2015.11.004

2015-06-22

黑龙江省科学技术基金资助项目(E051103)

李志鹏(1963—)，男，黑龙江哈尔滨人，博士，教授，主要从事汽车电子控制技术研究。

李志鹏，李晓英，邵宪友.基于COMSOL声表面波扭矩传感器的有限元分析［J］.重庆理工大学学报:自然科学版，2015(11):17-22.

format:LI Zhi-peng，LI Xiao-ying，SHAO Xian-you.Finite Element Analysis of Torque Sensor Based on COSMOL Surface Acoustic Wave［J］.Journal of Chongqing University of Technology:Natural Science，2015(11):17 -22.