《对数函数及其性质》(第一课时)教学设计
邢晓燕


● 创新整合点
◇运用几何画板软件的作图功能、动态演示功能、反射功能,突出学习重点、突破学习难点。设计“动手实践1”,运用作图功能,使学生在同一坐标系中绘出多个对数函数图像,提高学生动手实践能力,加深对对数函数定义的认识,突出学习重点;设计“动手实践2”,运用动态演示功能,呈现对数函数图像随底数的变化情况,验证底数取定义范围内任意值时,对数函数所具备的性质,增强学生对图像的直观感知,突破学习难点;设计课件,运用反射功能,验证函数与函数(且)图像间的对称性。
◇运用学霸机房管理系统,借助“广播教学”、“文件分发”、“学生演示”功能,实现图像共享,提高学习效率,突破学习难点。“广播教学”功能,实现教师集中授课与学生自主学习相结合;“文件分发”功能,将教师机课件分发至学生机D盘,快速便捷,避免一一拷贝;“学生演示”功能是小组代表发言活动得以实施的关键。如果没有学霸机房管理系统,学生所绘图像只能呈现在自己的计算机上,无法实现共享,而“学生演示”功能的使用,使得全班同学能快速共享大量图像,提高了学生对研究过程的参与程度,学习效率明显提高。
● 教材分析
本节课是《普通高中课程标准实验教科书·数学1(必修)》(人教A版)第二章第一节第二课《对数函数及其性质》。本节课的内容在教材中起到了承上启下的关键作用。一方面,对数函数是在学生系统学习了函数概念,基本掌握了函数性质的基础上,进行研究的第一个重要的基本初等函数。作为基本初等函数,它是继指数函数之后对高中函数概念及性质的又一次应用;另一方面,对数函数是后续学习幂函数的基础,对于研究幂函数及其他基本初等函数,在研究方法上起到示范作用。
● 学生分析
从学生的知识上看,学生已经学习了函数的定义、图像、性质,对函数的性质和图像的关系已经有了一定的认识。学生已经熟悉研究函数的一般过程和方法,会用此来研究对数函数。
从学生现有的学习能力看,通过初中对函数的认识与理解,学生已具备了一定的观察事物的能力,积累了一些研究问题的经验,初步具备了抽象、概括的能力。通过教师启发式引导,学生能自主探究完成本节课的学习,会进行几何画板的基本操作。
● 教学目标
知识与技能目标:①通过具体实例了解对数函数模型的实际背景;②初步理解对数函数的概念、图像和性质。
过程与方法目标:①借助几何画板绘制对数函数图像,加深对定义的认识,增强对对数函数图像的直观感知;②学生观察对数函数图像,通过小组讨论,代表发言等活动,探究对数函数性质;③通过对对数函数的研究,体会数形结合、由具体到一般及类比思想。
情感态度与价值观目标:通过小组讨论、代表发言活动,培养合作交流意识。
● 教学环境与准备
多媒体网络教室、几何画板课件、学霸机房管理软件。
● 教学过程
1.创设情境
观察事例1:某种细胞分裂时,由1个分裂成2个,2个分裂成4个,……依此类推,一个细胞分裂次后,得到的细胞个数为个,思考与的函数解析式:;指数式化对数式:,用表示自变量:。
观察事例2:一根1米长的绳子,第一次剪掉绳长的一半,第二次剪掉剩余绳长的一半,……剪了次后,剩余绳子的长度为米,思考与的函数解析式:;指数式化对数式:,用表示自变量:。
观察事例3:已知一个正方形的面积是1,第一次取其四分之一生成正方形,再取的四分之一生成,以此类推,求第次取后生成的正方形的面积与截取次数之间的函数解析式:;指数式化对数式:,用表示自变量:。
设计意图:课上播放PPT动画,回顾“指数函数及其性质”一节的三个观察示例:“细胞分裂”、“剪绳动画”、“截纸动画”,引出对数函数定义,同时使学生体会到对数函数与指数函数的联系。
2.探究新知
(1)归纳定义
问题1:上述观察事例中的三个函数解析式有什么共同特征?
学生思考得出,三个函数解析式,结构都是对数的形式,自变量在真数位置,定义域为。
设计意图:通过对三个实例函数解析式的分析,突出对底数取值的认识,引导学生把解析式概括为的形式,为形成对数函数定义作铺垫。
对数函数的定义:一般地,形如(且)的函数叫做对数函数,其中是自变量,函数的定义域为 。
师生共同分析定义要点:①定义域为;②对数函数是形式化的定义;③且。教师引导学生将指数函数定义与对数函数定义作对比。
练习1:根据对数函数定义,判断下列函数是否为对数函数。
设计意图:通过题目判断加深学生对对数函数定义的认识和理解,为学生自主选择底数,应用几何画板绘制对数函数图像作铺垫。
(2)作图探究
问题2:我们研究函数的一般过程是什么?
教师启发学生思考:归纳定义,画出图像,观察图像,总结性质,继而进行性质应用。
设计意图:对数函数作为基本初等函数,是继指数函数后对高中函数概念及性质的再次应用,学生已经熟悉研究函数的一般过程和方法,会用此来研究对数函数。
作图1:画出函数的图像。
学生独立在坐标纸上作图,教师巡视个别辅导,正投对比展示学生作圖结果,总结作图要点,规范列表、描点、连线的每一步。
设计意图:描点法作图是画函数图像的基本方法,用正投呈现学生作图结果,培养学生画图基本功。
作图2:自主选择底数绘制对数函数的图像。
教师:为了研究对数函数性质,我给同学们传送了几何画板课件“动手实践1”,在D盘,这里有两个任务,请相继完成。对于任务1,全班同学分为6组,小组中每位同学设想一个具体的对数函数解析式,小组汇总,每位同学在同一坐标系中,绘制每组所确定的对数函数的图像,之后完成任务2(如图1)。
设计意图:设计任务1,是为了加深学生对对数函数定义的认识,增强对图像的直观感知。设计任务2,是将本节课的重点以任务形式呈现,使任务1的实施更具方向性,使课堂教学更具灵活性和机动性。
每位学生自主选择底数,确定一个
对数函数解析式,小组汇总。
设计意图:学生自选底数,确定对数函数解析式,加深对对数函数定义的认识。
学生小组讨论之后,每位同学打开D盘,双击进入几何画板课件“动手实践1”,在同一坐标系中,绘制每组确定的对数函数图像。
设计意图:学生通过几何画板课件“动手实践1”,在同一坐标系中,绘制多个对数函数图像,在绘制过程中,可以更加直观地感知底数对对数函数图像的影响,能更好地观察图像特征,总结图像性质。
学生自主选择底数,绘制对数函数图像,完成“任务1”之后,思考、讨论“任务2”,各小组根据所绘制的对数函数图像,观察图像特征,总结性质,每组自荐一名代表发言。
教师适时发问、点拨,引导学生总结,师生、生生互动交流。
设计意图:应用学霸机房管理系统,“学生演示”功能,逐个呈现每组学生作图结果,快速大量共享图像,加深学生对对数函数图像特征的认识,有助于攻克教学难点,课堂效率明显提高。
小组学生发言,师生交流过程中,解决问题3、问题4和问题5。
问题3:观察图像,你认为如何对对数函数进行分类研究?
各小组学生共提出两类标准:①按图像上升和下降分两类;②按底数分两类。经教师引导,学生发现这两类标准可以统一:与图像上升统一;与图像下降统一。
问题4:你能结合屏幕上所呈现的对数函数图像,观察它们的图像特征,并总结其性质吗?
各组学生从图像位置、特殊点、图像变化趋势等方面总结图像特征,概括性质如表1。
设计意图:学生通过观察具体对数函数图像,应用数形结合思想,归纳概括性质。
问题5:函数与(且)的图像之间有什么关系?
有的小组作出和的图像,观察、猜想两个函数图像关于轴对称;有的小组作出3对对数函数图像(如图2),观察猜想图像关于轴对称,进而猜想与(且)关于轴对称。
对于学生猜想和的图像关于轴对称,教师引导学生从坐标角度理解,并用几何画板进行验证。在函数图像和函数的图像上,分别取横坐标相同的两个点,点和随之运动,观察纵坐标关系,发现纵坐标相反,点和关于轴对称,所以和的图像关于轴对称。继而,教师操作课件验证:当取定义范围内的任意值时,图像间的对称关系(如图3)。
设计意图:通过具体底数的两个对数函数图像间的关系,观察、归纳、概括一般的两个对数函数与(,且)图像间关系,体会由特殊到一般思想的应用。
各小组总结图像特征,概括函数性质之后,教师总结呈现整理结果。
问题6:我们由具体对数函数分析出它们的图像特征和所具备的性质,所有的对数函数都具备这样的性质吗?
教师操作几何画板软件,通过拖动点,改变底数的大小,得到(且)的对数函数的图像,验证底数取定义范围内所有值时,对数函数的性质。
在几何画板课件“动手实践2”中,学生自己拖动点“”,亲身体验图像随底数的变化情况,进而归纳性质(如图4)。
设计意图:通过几何画板课件的动态演示,学生更直观地观察到对数函数图像随底数的变化情况,以及为什么要把底数分为和两类,有利于学生由图像归纳性质,从而突破本节课的难点。
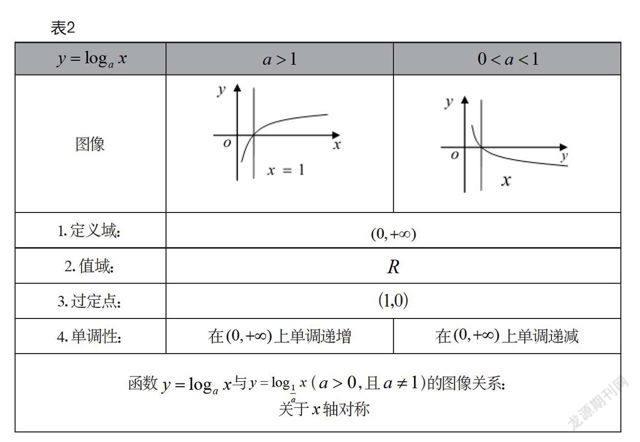
(3)归纳性质
學生观察图像,讨论总结性质,如下页表2。
设计意图:学生总结性质,培养学生归纳概括能力。
师生共同对学习内容进行总结:①研究函数的一般过程是:定义→图像→性质→应用。②借助图像研究性质,应用了数形结合思想;由具体对数函数入手,到一般对数函数总结性质,应用由特殊到一般思想方法;对数函数对底数分类进行研究性质,应用了分类讨论思想,类比指数函数研究对数函数,应用了类比思想。
3.例题讲解
师:刚才我们共同探究得出性质,下边看性质应用。
例1:比较下列各组中两个值的大小:①;②;③。
设计意图:通过例题使学生体会对数函数单调性应用,设计三题,使学生体会分类讨论思想。
第一题教师引导讲解,示范解答过程,第二题、第三题学生正投讲解。
设计意图:通过学生正投讲解题目做法,培养学生学习数学的信心和勇气,同时,对于出现的错误及时纠错,起到示范作用。
4.归纳总结
◇这节课你学到哪些知识?
◇这节课你体会到哪些数学思想方法?
5.分层作业
◇必做题:P73,2、3;
◇选作题:函数和的图像间有何关系?
● 教学反思
1.设计问题系列,驱动教学
问题是数学的心脏,本节课以6个问题为主线贯穿始终,以问题解决为教学线索,在教师的主导与计算机的辅助下,学生思维由问题开始,由问题深化。
2.借助信息技术突出重点、突破难点
本节课的学习重点是对数函数的概念、图像和性质;学习难点是用数形结合方法从具体到一般地探索概括对数函数性质,为突出重点、突破难点,使用了以下信息技术:
◇探究对数函数概念:课上播放“细胞分裂”、“剪绳动画”、“截纸动画”三个PPT课件,学生总结三个“观察事例”中函数解析式的共同特征,概括到的形式,从而形成概念,突出学习重点。
◇绘制对数函数图像:作图1,学生动手画图,初步感知对数函数图像,教师个别辅导,正投展示,对比分析作图结果,纠正作图错误,总结作图要点,培养学生作图基本功;作图2,设计课件,全体学生参与,自选底数绘制对数函数图像,从而加深了学生对定义的认识,增强了对图像的直观感知,突出学习重点。
◇探究对数函数性质:对数函数性质的获得,需要借助对数函数图像。设计“动手实践2”,教师运用几何画板的动态演示功能,验证底数取定义范围内所有值时,对数函数的性质,学生操作课件“动手实践2”,通过拖动点“”,改变底数的值,观察对数函数图像随底数的变化情况,学生的亲身体验,提高了对研究过程的参与程度,有效突破学习难点。
◇运用学霸机房管理系统,其“广播教学”“文件分发”“学生演示”功能,使得大量图像共享成为可能,使得学生小组代表发言活动得以实施。学霸机房管理系统的使用,提高了学生对研究过程的参与程度,使得学习效率明显提高,更为有效地突破学习难点。

