二次函数图象 “五步法”教学例谈

唐庆玲

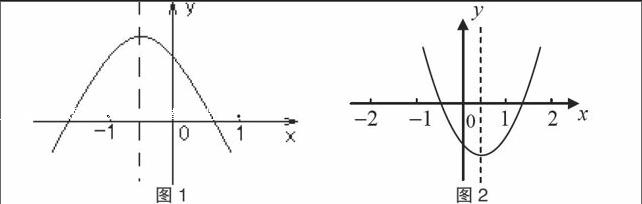
摘 要：二次函数图象是初中数学教学中重要的内容之一，数学教师必须认真阅读教材，吃透原理，通过各种策略和方法有效唤起学生学习的积极性，从而不断培养学生发现问题、分析问题、解决问题的综合能力。

关键词：二次函数图象；探究式重组；“五步法” 例谈

在多年的教学实践中，我发现教材中描点法画二次函数y=ax2+bx+c（a≠0，a，b，c都是常数）的图象存在一些问题值得我们商榷：一是在抛物线图象上存在最高点或最低点，如果学生在描点时找不到这个点，那么再多的点也是无用；二是在抛物线上存在几个重要的点，例如：y轴交点、x轴交点、对称轴、顶点坐标，学生如果不能很好的运用这些点，将给以后学习二次函数带来隐患；三是二次函数的图象和性质有着十分广泛的应用，教材把图象画法与图象增减性放在一起，导致课堂容量过大，学生不能很好地掌握；四是学生的认知已清楚二次函数的图象是抛物线，只是不确定要将抛物线放在坐标系的何处而已，故我们可以探讨寻求其它的画图方法来推进知识的理解和运用。

鉴于以上原因，我对教材进行了探究式重组，放弃“唯书论”“唯师论”，利用了“五步法”画抛物线，这样，不仅符合学生的认知规律，而且还使学生进一步体会了数形结合的思想方法，学生通过自主操作、合作交流、在猜想与探究的过程中逐步掌握了数形结合思想，同时也充实了课本内容，锻炼了学生思维，培养了他们实践的能力和推理能力，最终提升解决问题的能力。下面我根据教学实际和经验探索来谈谈自己的几点认识。

一、引导探究，归纳关键知识点

我认为：教材呈现和所强调内容的逻辑性、严密性与科学性是合理的，但是在教学实践中适当地对教材做点变通和改变，以便能让学生更好地理解和接受知识那才是最好的。从建构主义的理论观点出发，教师在实际教学中选取的内容多少，容量大小应该由学生的实际情况来确定，也就是说我们在教学中要尊重学生各自的经验、思维方式和习惯，积极组织和引导学生观察、探究、发现。虽然最终结论是一致的，但学生解决问题的过程可以是多元的。

在教学中，我先让学生回顾y=ax2，y=ax2+c，y=a（x-h）2+k的图象，并说出这些图象的共性与区别，然后再让学生猜想y=ax2+bx+c的图象。一番讨论之后，在黑板上画出两条抛物线，如图1、图2所示：

先让学生认识这就是二次函数y=ax +bx+c图象，也叫做抛物线，再要求学生结合一次函数图象画法仔细观察对比两个图，接着我提出以下两个问题：（1）如果你们自己画，需要注意哪些关键点？（2）抛物线是否是轴对称图形？

学生根据教师提出的问题，小组讨论，同学间互相交流补充，教师积极引导，学生主动参与。由于学生已经学习过一次函数，反比例函数，所以学生对函数图象有较强的认知能力，在思考的过程中，学生逐步形成认知，教师再根据学生的回答和学生一起归纳出以下关键点：（1）抛物线与x轴的交点。（2）抛物线与y轴的交点。（3）抛物线的最高点或最低点。（4）抛物线的对称轴。（5）抛物线开口方向。

评析：学生会有其他回答，教师要做引导、分析、解释。在备课时要尽量考虑周到，既要备教材，又要备学生，还要重视知识的生成过程，在教学设计中，教师可以预设多种可能。

二、创设问题情境，重视知识的生成过程

教师对教材的理解，不但要理解知识内容，更要理解其中蕴含的数学思想方法，以及学生的情感态度和价值观，并在适当的时机展示数学美，欣赏数学美。因此我在完成归纳总结后，要求学生以小组形式完成y=x2-2x-3的图象，采用的方式是学生独立完成与共同探讨相结合，让学生自己动手，大胆展示，畅所欲言，表达自己的想法，激发学生认知的欲望，当学生讨论分歧达到最高点时，我抓住时机，引导学生回顾以上五点，按下面五个步骤完成观察、分析、概括。

教师板书：

第一步：令y=0，即x2-2x-3=0 解可得x=-1或x=3

所以抛物线与x轴交点为A（-1，0），B（3，0）

第二步：令x=0 即y=-3

所以抛物线与y轴交点为C（0，-3）

第三步：到这里我让学生利用配方法求二次三项式最大值或最小值做了必要的回顾，随后让学生完成配方：y=x2-2x-3=x2-2x+1-1-3=（x-1）2-4，学生容易得出当x=1时，y有最小值-4，即抛物线最低点D（1，-4），学生对比图1、图2得到对称轴：x=1。

第四步：要求学生用光滑曲线连接上面的点，提醒学生注意对称性。随即可以得到y=x2-2x-3的图象，如图3所示。

引导学生用关键点画出函数图象，让不同层次的学生展示自己画的图象，同时进行比较，让他们弄清自己所画的不足之处，并在比较中深化知识的理解。实践证明，学生对此知识点会掌握地更好。

第五步：学生小组合作画出下列二次函数图象：

①y=x2-x-2 ②y=-x2+x+2

完成之后，教师引导学生做出抛物线开口方向的判断：a>0，开口向上；a<0，开口向下。

评析：二次函数的图象本来就广泛应用于生活和生产中，例如：拱桥，投篮，投铅球，花园里的自动喷水器等，它们都是学生熟悉的图形，它们既有对称美又有实用价值。如果能将传授知识与欣赏美、感受美相结合，那么数学课堂教学也将是美的。至此，“五步法”操作基本完成。

四、总结反思，做好铺垫

本节课，解决了二次函数中很多关键问题，如二次函数与坐标轴的交点的求法，利用配方法求二次函数最高点或最低点问题（事实上就是顶点和最大值或最小值问题）。为下节课函数性质的得出做了很好的铺垫，为学生继续学习二次函数打下良好的基础。我没有像教材中那样更多的强调抛物线的顶点和二次函数最大或最小值之间的关系，也没有涉及二次函数增减性，而是根据自己学生的实际情况把它们放到下一课时。

总之，一个善于思考，爱动脑筋的教师，才能在教学中汲取课本精华，并将课本所蕴含的数学思想方法，技能技巧传授给学生，提炼并总结出学生易于理解和操作的数学方法。只有这样，教师的“教”才能促进学生的“学”。叶圣陶先生说：“教材只能用为教课的依据，要教得好，使学生受到实益，还靠教师的善于运用”。教材是对话的文本，是学生学习活动所凭借的话题与依据，教师应钻研教材，领悟教材的编写意图，必要时可在教学过程中重组教材，让教材变为一个动态生成的、鲜活实效的教学内容，以达到教材使用的最高层次——超越教材。这样，教师才能凭借教材，整体使用教材，才能促进学生数学素质的全面发展。

参考文献：

[1]《全日制义务教育数学课程标准（修订稿）》 北京师范大学出版社 2013年6月.

[2]席振伟著《数学的思维方式》 江苏教育出版社 2009年5月.endprint