经典全等图形的变式问题解读

☉江苏省苏州市相城区春申中学 丁 岩

经典全等图形的变式问题解读

☉江苏省苏州市相城区春申中学 丁 岩

变式教学是我国中学数学教学中的重要方式，特别是关于习题的变式，具体到每一节数学课堂、每一次课后作业、每一份数学试卷，无不体现着习题变式的追求，然而变式的方向、意图、立意却各不相同，层次也高低不等．本文选择平面几何初学全等时的经典图形，变式追问，意图指向后续学习，与同行研讨交流．

一、全等图形的变式题例

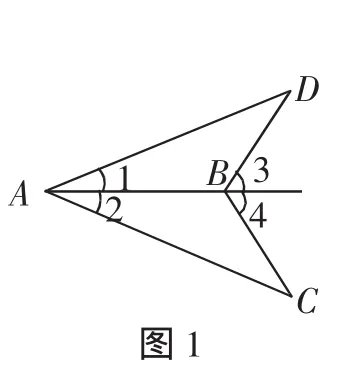
例1 如图1，∠1＝∠2，∠3＝∠4．（1）求证：AC＝AD．

（2）过点B作BG⊥AD，BH⊥AC，垂足分别为G、H．求证：BG＝BH．

变式解读：第（1）问是很多教材上的经典全等习题，主要是促进学生转化间接条件“∠3＝∠4”，而不能直接使用．根据教学经验，不少几何学习适应性不好的学生，往往将间接条件“∠3＝∠4”直接使用，需要多次提醒、训练才能达到规范要求；而第（2）问则是要求学生作图，然后证明三角形全等得出“角平分线上的点到角的两边距离相等”，实质上是后续要学习的角平分线性质定理．

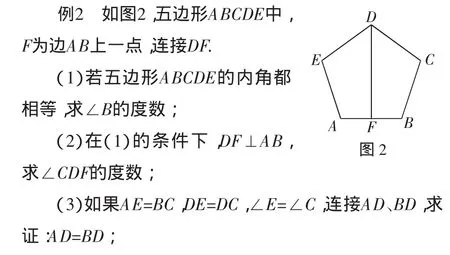
（4）在（3）的条件下，若DF⊥AB，点F是否为AB的中点？为什么？

（5） 如果DF垂直平分AB，且AE＝BC，∠EAB＝∠CBA，求证：DE＝DC．

成果扩大：小舟练习之后，发现在（5）的条件下，还可以证明四边形AEDF≌四边形BCDF！

你会证明小舟的发现吗？

变式解读：这是七年级初学多边形内角和性质时就有的一道经典正五边形问题，经过变式设问，将该题引向全等三角形的判定；重要的是，该题将会与后续学习等腰三角形的判定与性质建立关联．

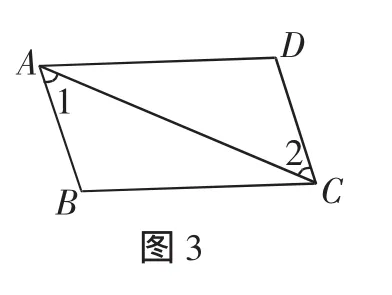
例3 如图3，在四边形ABCD中，∠B＝∠D，连接对角线AC，∠1＝∠2．

（1）问：边BC与AD有怎样的关系？并说明理由.

（2）连接BD，与AC交于O点，小诚发现：这个四边形的对角线竟能互相平分！你能证明小诚的发现吗？

变式解读：该题第（1）问主要是训练全等三角形的判定，而且是一种旋转180°后的对应关系，根据教学经验，不少全等适应性不佳的学生初学时往往难以找准对应关系；而第（2）问则将问题引向后续要学习的平行四边形的性质（平行四边形对角线互相平分）．

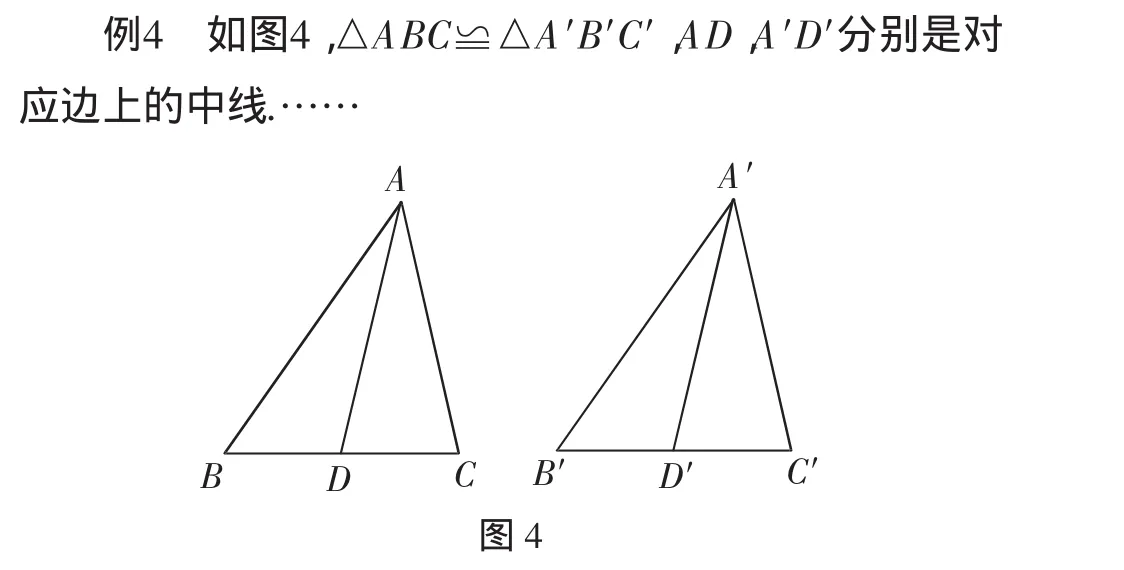
小诚很快证得AD＝A′D′．（结论①）

他想起老师说过“求出解答并继续前进”，是不是还能“成果扩大”呢？不一会儿，小诚就发现了BC、B′C′边上的高AH、A′H′的数量关系，也有AH＝A′H′．（结论②）

小南进一步猜想△ABC和△A′B′C′的对应角平分线BE、B′E′的关系，有BE＝B′E′．（结论③）

小史在他们在基础上，归纳出一个重要性质：如果两个三角形全等，那么这两个三角形中的对应线段一定相等．

小舟还不满足他们的发现，继续进行了如下探索，分别在边BC、B′C′上取一点M、M′，使BM＝B′M′，再连接AM、A′M′，则一定有AM＝A′M′．（结论④）

逆向思考，成果扩大：小婧想了想，是不是还能逆向思考呢？比如将题设与结论互换呢？她提出如下问题：

如图1，在△ABC和△A′B′C′中，AB＝A′B′，AC＝A′C′，AD、A′D′分别是边BC、B′C′上的中线，且AD＝A′D′．求证：△ABC≌△A′B′C′．（命题⑤）

……

答题要求：请证明上述“结论①、②、③、④”“命题⑤”．

变式解读：这道题主要向学生传递“求出答案并继续前进”（舍费尔德语），即全等三角形不仅是对应边、对应角相等，而且可以进一步成果扩大：全等三角形对应线段相等，而且通过模拟学生的探究对话，将问题深入；特别是最后一问，引导学生逆向思考，探究原命题与逆命题的关系，这又是一种成果扩大的探究取向；最后那个“……”将问题开放，让学生继续沿着小婧同学的思绪往前探究，比如还可提出“两个三角形的两边及第三边上的高对应相等，两个三角形全等吗”等问题．

二、变式立意的进一步阐释

以上选择近期改编的一题全等经典问题，并逐题给出命题解读，下面再从整体上阐释全等经典问题的变式立意．

1.深刻理解教学内容，精心选择经典问题

根据马立平博士的“深刻理解数学知识”的观点，选择哪些经典图形展开变式之前，需要基于“深刻理解教学内容”，认真思考哪些问题或图形是经典问题，具有较大的生长或拓展空间．上文提供的4个例题中，图形都比较简洁，较容易拓展生长，也是各类各级命题的重点图形．此外，精心选择经典问题也是后续预设追问的前提，因为一个问题如果不够典型，其生长性、讲评意义也不会很大，如“例1”那样，正是因为考虑到不少学有困难的学生常常在初学全等时，对于间接条件的错用、混用，才重新引导他们认真思考、训练这类问题，这也是落实双基的需要．

2.题干条件简洁呈现，预设追问自然生长

章建跃教授在文1中指出：“真正的数学题应该满足一些基本条件，例如：反映数学本质，与重要的数学概念和性质相关，不纠缠于细枝末节，体现基础知识和联系性，解题方法自然、多样，具有发展性，表述形式简洁、流畅且好懂等．”从上面提供的4个例题来看，题干条件都比较简洁、好懂，后续追问也显得自然、和谐，想要圆满完成又具有一定的挑战性．需要指出的是，习题变式时切忌在题目呈现初始阶段就是安排一个繁杂的图形，因为上来就是一个繁杂图形呈现时，往往有不少几何适应性不好的学生就会被拒之门外，习题的内容效度就大打折扣．

3.问题凸显几何特征，变式设问指向后续

根据中科院李文林研究员的观点，数学主要是“算”“证”．初中几何主要训练“证”的能力，发展逻辑思维能力，所以在选择几何图形问题及变式训练时，需要注意凸显几何学段特征，重视发展学生的几何推理论证能力．这也是我们在上述4个题例中重点构思的，此外，例1中的第（2）问指向后续即将学习的角平分线性质；例2中的第（4）、（5）问指向后续垂直平分线性质定理；例3中第（2）问指向后续要研究平行四边形的性质；例4中系列设问既训练巩固了全等三角形的判定方法，又示范了几何问题的研究套路和探究方向，既照应了学生的眼前利益，又关注了学生的长远利益．

三、写在最后

数学习题的变式设问是一个大的方向，是值得很多一线教师深入实践和思考的，我们在上面选择了日常教学中一些变式题例，阐释变式立意，这些努力是初步的，期待同行批评指正、实践跟进．

1.章建跃．发挥数学的内在力量，为学生谋取长期利益［J］．数学通报，2013（2）.H