深刻理解教学内容，预设追问促进生成——以“勾股定理”教学设计为例

☉江苏省南通市启秀中学 吴 敏

深刻理解教学内容，预设追问促进生成
——以“勾股定理”教学设计为例

☉江苏省南通市启秀中学 吴 敏

文1、文2分别从实验教学、操作拼图的角度对勾股定理起始课教学给出富有启发的教学设计，受此启发，笔者也将近期执教的一节“勾股定理”的教学设计梳理如下，并解读各栏目的设计意图，提供研讨．

一、勾股定理教学设计

1.结合历史，引出特例

情境引入：古希腊数学家毕达哥拉斯在朋友聚会时，发现脚下的地砖具有某种性质（如图1）．

预设：毕达哥拉斯发现等腰直角三角形三边之间的数量关系．

板书：命题1：如果直角三角形的两直角边分别为a和a，斜边长为c，那么a2+a2=c2.

2.探究发现，形成猜想

问题：毕达哥拉斯在发现了等腰直角三角形的三边具有这样的关系后，又进一步地往下思考．同学们，你们知道毕达哥拉斯又在思考什么吗？

预设：等腰直角三角形是特殊的直角三角形，应该考虑一般的直角三角形是否也有这样的结论．

板书：命题2：如果直角三角形的两直角边分别为a和b，斜边长为c，则有a2+b2=c2.

预设：如图2，提供方格纸（每个小正方形方格的面积均为1），在方格纸上有一个非等腰的直角三角形．设它的两条直角边分别为a和b，斜边为c，那么我们现在仍然用面积法来证c2=a2+b2，也就是要证明什么？（SA+SB=SC）

问题1：你如何计算图2中正方形A、B的面积？（数格子即可）

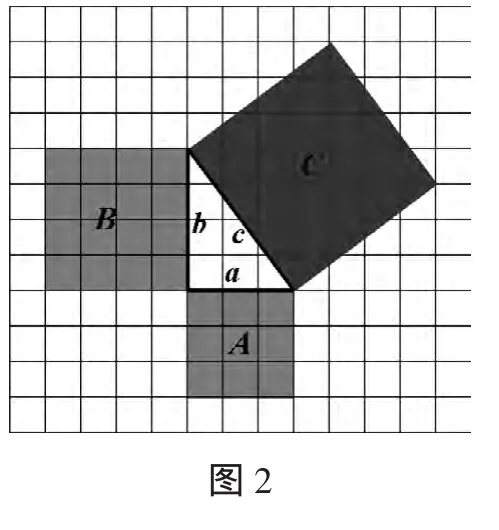
问题2：你如何计算图2中正方形C的面积？由此可知什么结论？（两种方法：割或补．其中割法即为弦图，可由学生讨论）

追问：这样我们能不能说这个命题得到证明了呢？如果是另外的情况，能否也用刚才的方法来说明呢？（不行，因为无法利用方格图了）

3.利用弦图，证明命题

介绍勾股弦图，为了研究的需要，标注一些字母，即两个边长分别为a和b的正方形拼成一个图形.

问题1：如图3，这时图形的面积为多少？（a2+b2）

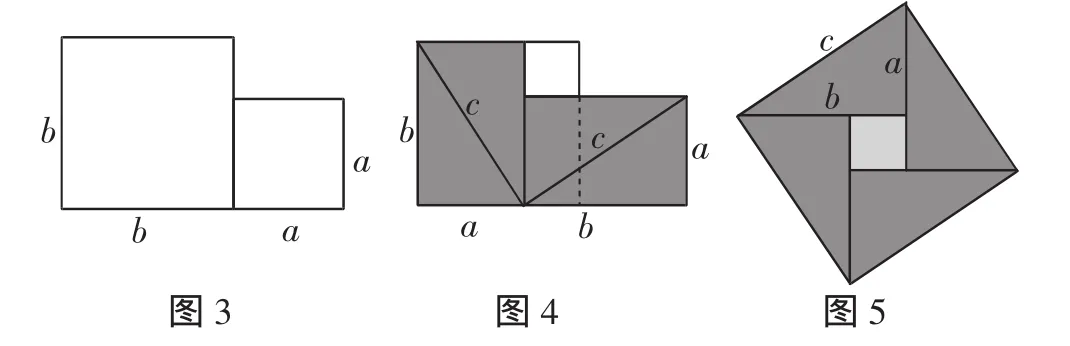
如图4所示，割出两个边长均为a和b的长方形；将这两个长方形分割成两个全等的直角三角形，这些直角三角形都是全等的，并且它们的直角边均为a和b，斜边我们设为c；将其中的两个直角三角形绕顶点旋转至如图5位置．

问题2：这时形成了什么图形？（正方形，并简要证明，并说明这个图形就叫“弦图”）边长是什么？（c）面积是多少？（c2）

预设：可以得出什么结论？（拼成的正方形面积等于原边长为a、b的两个正方形面积之和，即a2+b2=c2）于是我们通过对图形割补拼的方法，利用面积的关系，证明了命题1是真命题．我国古代把直角三角形中较短的直角边称为“勾”，较长的直角边称为“股”，因此我国将其称为“勾股定理”．

板书：将“命题2”改成“勾股定理”．

勾股定理：如果直角三角形的两直角边分别为a和b，斜边长为c，则有a2+b2=c2.

4.讨论交流毕达哥拉斯证法

介绍：毕达哥拉斯学派也用类似的方法证明过勾股定理，他们是利用四个以a和b为直角边，c为斜边的直角三角形（如图6），三个分别以a、b、c为边的正方形（如图7）.拼成两个面积相等的正方形（如图8、9）.

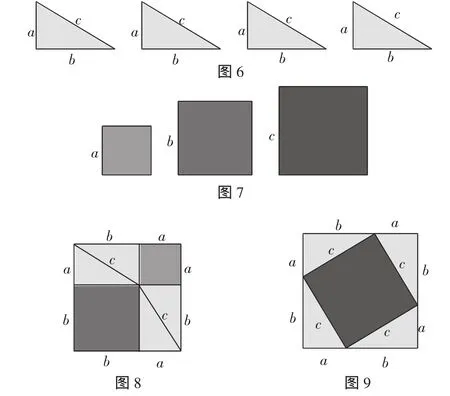
问题：你能否利用这两个图形来证明勾股定理吗？（用两个图形或只用右边一个均可证明，用一个图形证明需要有乘法公式的基础）

5.定理分析，简单运用

问题1：定理的题设是什么？（直角三角形，∠C=90°：反映“形”）结论是什么？（a2+b2=c2：反映“数”）因此勾股定理是“数”“形”结合的一个数学模型.

勾股定理的公式：a2+b2=c2是一个不定方程，解有无数个，若知道直角三角形的两条边，就可以求第三边.

二、教学设计的整体解读

1.深刻理解教学内容，挖掘勾股定理的人文价值

本节课是人教版（义务教育课程标准数学实验教科书）八年级（下）“勾股定理”第1课时，是直角三角形相关知识的延续，同时也是学生学习解直角三角形和学习锐角三角函数的基础，充分体现了数学知识承前启后的紧密相关性、连续性.勾股定理是几何中最重要的定理之一，揭示了直角三角形三边之间的一种数量关系，为发展学生的数形结合思想提供了思维平台.此外，历史上勾股定理的发现反映了人类杰出的智慧，勾股定理在数学的发展与现实世界中有着广泛的作用，其中蕴含着丰富的科学和人文价值，对于激励学生对数学学习产生兴趣具有重要意义.从研究方法而言，勾股定理的探索发现过程，是从特殊到一般的认识过程，学习用以“形”证“数”的方法证明勾股定理，是“数”与“形”相结合的一个数学模型，有利于培养学生的合理猜想能力，拓展学生推理论证的视野.

2.从理解学生的角度出发，预设教学活动和跟进追问

八年级学生已经具备一定的观察、归纳、探索和推理的能力.在小学已经学习了几何图形面积的计算方法——割补法，但运用面积法和割补思想解决问题的意识和能力还远远不够.部分学生听说过“勾三股四弦五”，但并没有真正认识什么是“勾股定理”.本节课的学习重点在于勾股定理的证明，而证明的思想大部分都基于面积的割补拼接，多媒体的作用即体现于此，利用形象的PPT动画向学生演示弦图的生成过程，有利于学生在自己的大脑中对思考内容进行比较和验证，加深对面积法的印象与理解.

3.加强教学对话、互动生成，注重数学思想方法渗透

从上面的教学设计来看，我们预设了大量的互动式的教学活动，并积极与学生对话，促进教学生成；同时在与学生对话、追问之中，引导学生体会、感受数学思想方法，比如从等腰直角三角形到一般直角三角形，渗透了从特殊到一般的数学思想.在勾股定理证明之后，引导学生思考勾股定理揭示出的“形”“数”之间的关系，渗透数形结合思想.

三、结束语

勾股定理是千古第一定理，她的教学更是很多同行研讨的热点，文2中曾说“要想看一个数学教师的基本功，就让他教勾股定理”，此言不虚，我们对勾股定理教学的探索实践只是开始，远未结束，将来的教学生活中还会碰到，还要加强研讨，争取更深刻地理解教学内容，预设出既贴近学生实际，又过渡自然的教学设计.

1.万广磊．基于数学实验的勾股定理教学实践［J］．中学数学（下），2015（4）.

2.冒劼．有效先学·踊跃展示·启发思考——勾股定理（第1课时）教学设计与解读［J］．中学数学（下），2015（7）.Z