一道竞赛题的再探究

☉重庆市云阳江口中学校 王连娜 姜官扬

一道竞赛题的再探究

☉重庆市云阳江口中学校 王连娜 姜官扬

一、赛题呈现

题目 （2011年北京市初二数学竞赛题）如图1，边长为1的正方形EHGF在边长为3的正方形ABCD所在的平面上移动，始终保持EF∥AB.线段CF的中点为M，DH的中点为N，则线段MN的长为（ ）.

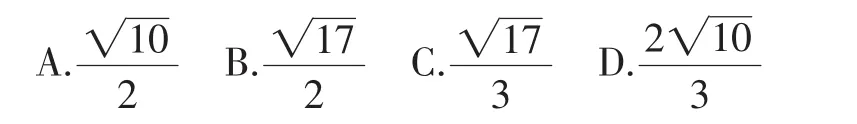
文1用三种不同的方法完成了解答，并且给出了八个不同的变式.读后感想颇多，掩卷之余，总有意犹未尽之感，因此，对如下两点进行了再思考和探究：一是变式的解答，二是原题的变式题是否只有文1给出的八种情况.现将对这两点的思考所得，整理成文，呈现于此，供参考.

二、几个变式的再解

此解法与文1给出的解法相比，不仅少作了辅助线，而且所用的知识较少，思路自然流畅.

此解法与原解法相比，少作了两条辅助线，且用到的知识点少，过程也简洁得多.

此解法比原解法少作两条辅助线，且解题过程简单明了.

三、变式再探

经过探究发现，除文1给出的8个变式之外，还能得出许多优美有趣的变式题，现略举几例.

因为原题中要求边EF与边AB平行，若将此要求改为对角线EG与边AB平行，其余条件不变，又可得：

若将原题中的一个（或两个）正方形改为矩形、菱形或平行四边形，其余条件不变，以及在变式18、19、20的基础之上，还能得出许多变式题，限于篇幅，就不一一例举.

四、由原题、变式题编出新题

1.由原题编出新题

原题为选择题，而选择题反映不出学生的思维过程，为了考查学生的思维过程，可以将原题改编为：

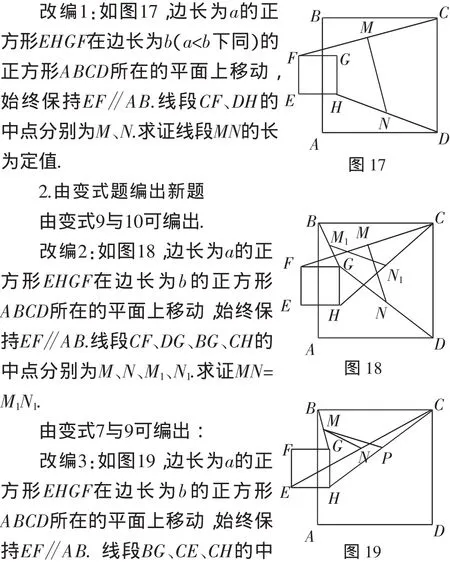
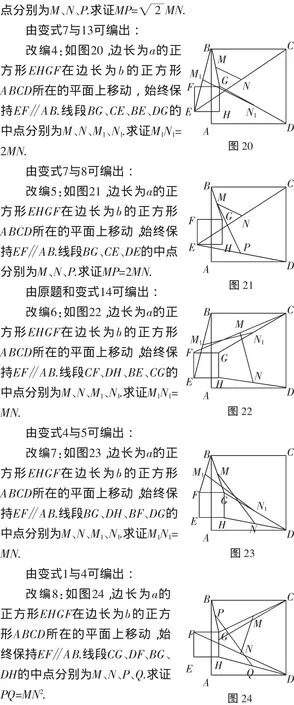
这些题的证明，限于篇幅，此处略去.

由原题和变式题还能编出许多新题，不再赘述，请有兴趣的读者自己去探讨之.

1.张宁.一道竞赛题的解法及变式探究［J］.中学数学（下），2015（4）.H