在“折叠”中体会数学的奥妙

☉江苏省苏州市高新区实验初级中学 朱秋芳

在“折叠”中体会数学的奥妙

☉江苏省苏州市高新区实验初级中学 朱秋芳

有关折叠问题在近几年各地中考中频频出现，有图形折叠后再剪裁并判断剪裁后图形形状的、有图形折叠后求折痕或其他线段长度的、有图形折叠后求边或角的大小关系的、有图形折叠若干次后寻找折叠前后变化规律的、还有坐标系下的图形折叠题等.由直接运用折叠相关性质的说理计算题，发展到基于折叠操作的综合题，甚至是压轴题.考查的着眼点日趋灵活，能力立意的意图日渐明显.

一、几个常见的剪纸活动中初步体会折叠的特殊运用

1.折纸剪裁正方形

把矩形纸片按如图1折叠，就可裁出正方形纸片.

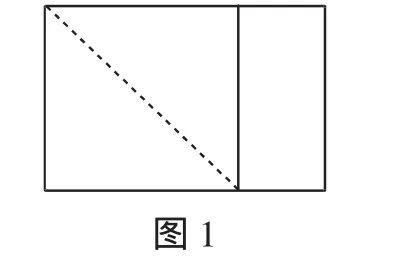
2.折纸剪裁菱形

将矩形纸片对折再对折，然后沿着图2中的虚线剪下，就可裁出菱形纸片.

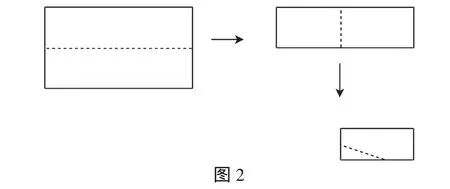
3.折纸做等边三角形

如图3，对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展平，再次折叠纸片，使A点落在折痕EF上的N点处，并使折

痕经过点B得到折痕BM，接下来只要再沿MN所在的直线折叠一次就可以裁出等边三角形了.

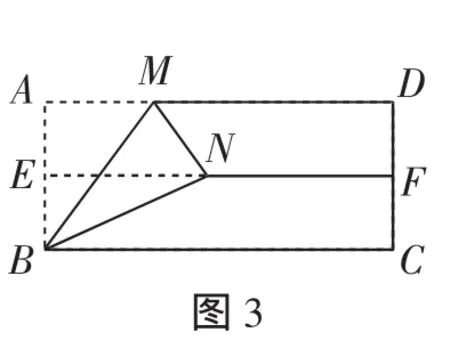
二、常见的折叠问题

1.几何图形通过折叠后求折痕或其他线段长度

解决折叠问题，首先要对图形折叠有一个准确定位，把握折叠的实质；还要在变换几何图形的位置、形状、大小后找到图形之间的联系，知道哪些量没变、哪些量已改变.例如：折叠问题中折叠前后图形全等是解决问题的关键，图形折叠问题中蕴含着重要的轴对称知识，因此，解决这类问题的关键是弄清折痕（即对称轴）及其两侧的全等图形；然后利用勾股定理和相似三角形的性质进行推理、计算.

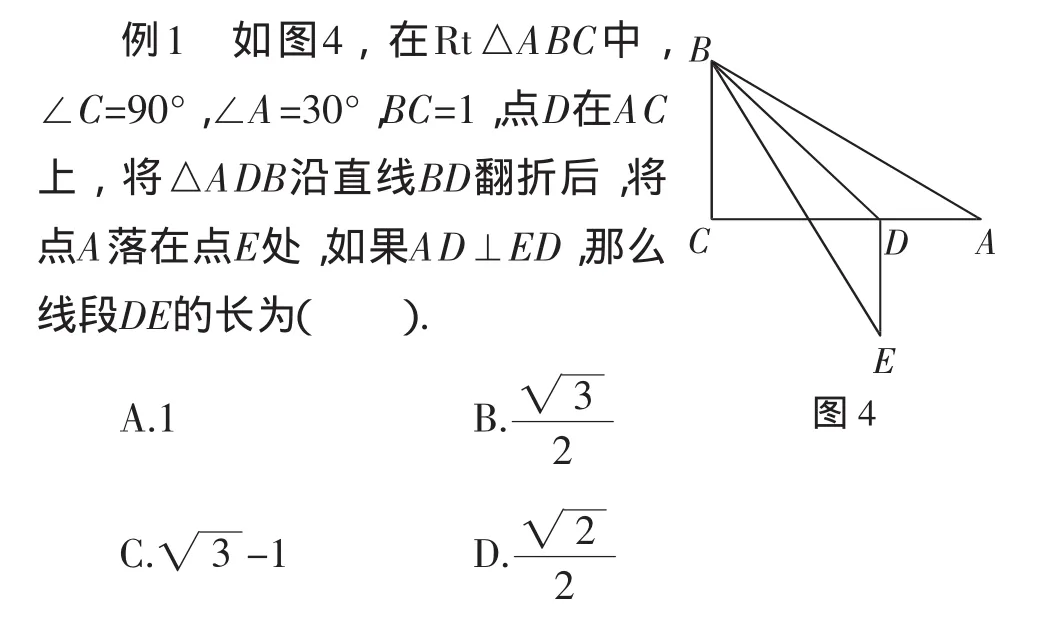
思路分析：由在Rt△ABC中，∠C=90°，∠A=30°，BC=1，利用三角函数，即可求得AC的长，又由△ADB沿直线BD翻折后，将点A落在点E处，AD⊥ED，根据折叠的性质与垂直的定义，即可求得∠EDB与∠CDB的度数，继而可得△BCD是等腰直角三角形，求得CD的长，继而可求得答案.解答过程略.

反思：本题充分利用折叠的性质，结合直角三角形中的勾股定理等知识点，运用数形结合的方法，最后求出未知线段，一定要注意折叠前后图形中角及边的对应关系.

反思：此题主要考查了折叠对称的性质、勾股定理、等腰梯形的判定与性质.从本题可以看出：对称点的连线被对称轴垂直平分，连接两对称点既可以得到相等的线段，也可以构造直角三角形，把折叠问题与四边形的知识结合，联系了折痕与四边形形状之间的互推；考查了学生的应变能力与动手操作、空间思维能力，较好地体现了折叠问题的全面性与技巧性.

2.圆或圆的一部分通过折叠后求有关弧长或面积的问题

例3 如图5，AB是半圆O的直径，且AB=8，点C为半圆上的一点.将此半圆沿BC所在的直线折叠，若圆弧BC恰好过圆心O，则图中阴影部分的面积是_________.（结果保留π）

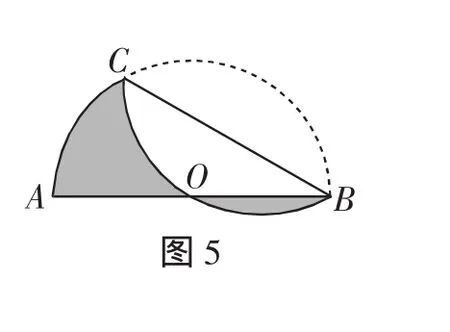
反思：解题过程似乎不难，但要求学生的思路一定要非常清晰，始终紧扣题意，抓住实质，考验了学生严谨、细致的求学态度.

例4 如图6，在扇形OAB中，∠AOB=110°，半径OA=18，将扇形OAB沿过点B的直线折叠，点O恰好落在上的点D处，折痕交OA于点C，则的长为_________.

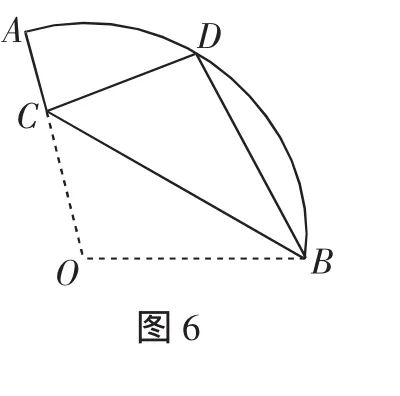
思路分析与解答：如图6，连接OD.根据折叠的性质、圆的性质推知△ODB是等边三角形，易求∠AOD=110°-∠DOB=50°；然后由弧长公式l=来求的长，所以由折叠的性质推知△ODB是等边三角形是解答此题的关键之处.

3.图形折叠若干次后寻找折叠前后的变化规律

实际解决问题时有些题型通常会出现折叠多次的情况，这样就需要寻找多次折叠之间的规律了.

反思：本题主要熟悉沿对称轴折叠后的图形与原图形相似的特征，又要利用等腰直角三角形的特殊性，得出规律.

4.平面直角坐标系下的几何图形的折叠

平面直角坐标系下图形折叠型压轴题的新颖、灵活之处在于不但要会抓住折叠后图形的性质，还要求具有较强的想象力进行合理猜想；还要善于应用有关数学知识进行运算和逻辑推理，验证猜想.

例6 如图8，平面直角坐标系中有一张矩形纸片OABC，O为坐标原点，A点坐标为（10，0），C点坐标为（0，6），D是BC边上的动点（与点B、C不重合），现将△COD沿OD边翻折，得到△FOD，再在AB边上选取适当的点E，将△BDE沿DE翻折，得到△GDE，并使直线DG、DF重合.

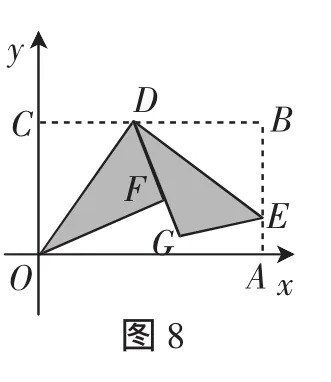
反思：本题用到了折叠后三角形全等求线段长及点的坐标；由相似三角形的性质建立二次函数模型求最值；一元二次方程根的判别式确定函数图像交点个数，证明猜想，解决此类压轴大题，也充分考验了学生的空间想象能力与综合素质.

总之，图形的折叠问题是图形变化的一种，主要是考查学生的自主探索能力、空间想象能力及判断推理能力，也有利于培养同学们的创新能力和实践能力.我们要想在众多折叠题中显得游刃有余，那就一定要抓住“折叠”的实质，展现数学中的“奥妙”所在.相信我们一定能用双手“折叠”出美丽的世界，也能用心灵创造出美好的未来.

1.吴行民.“轴对称”牵手“折叠”［J］.中学生数学（初中版），2010（9）.

2.陈轶.浅议“问题教学”［J］.吉林教育，2010（19）.Z