线段长度“参数化”，方程函数助求值——2015年江苏连云港卷把关题的思路突破与解后反思

☉江苏省苏州市阳山实验初级中学校 仲进东

线段长度“参数化”，方程函数助求值
——2015年江苏连云港卷把关题的思路突破与解后反思

☉江苏省苏州市阳山实验初级中学校 仲进东

近年来，一类以“函数图像+几何性质”为载体的中考压轴题较为流行，这类问题常常与动点问题、存在性问题、最值问题综合在一起，让不少学生感觉到困难，也成为中考二轮复习的重点.下面选取一道2015年中考题，帮助大家突破思路，并一起反思这类问题的解题关键：线段长度“参数化”，方程函数助求值.

一、考题及思路突破

（2）在x轴上是否存在点C，使得△ABC是直角三角形？若存在，求出点C的坐标；如不存在，请说明理由.

（3）过线段AB上一点P，作PM//x轴，交抛物线于点M，点M在第一象限，点N（0，1），当点M的横坐标为何值时，MN+3MP的长度最大？最大值是多少？

思路突破：（1）比较基础，只要找出两个点的坐标就能确定直线解析式，而题目已给定点（0，4）；另外尝试利用抛物线的解析式确定A点坐标为（-2，1），就能利用待定系数法明确直线解析式了.

（2）这里看似是一道以抛物线为载体的存在性问题，本质上与抛物线无关，因为A、B点都已被确定，本质上就是已知两个定点，在x轴上寻找一点，使这三个点围成直角三角形.这类问题分三种情况讨论：分别以A、B、C为直角顶点讨论，用一个参数式子分别表示AB、AC、BC，再结合勾股定理得出方程求解.

（3）又是一个动点P，要注意点P在“线段AB”上，即点P的横坐标是有取值范围的！待求的“MN+3MP”也很难找到转化成某一条直线的模式或解题经验，那就设法用一个参数分别表示这两条线段的长，然后再转化为一个函数表达式，分析最值.3a+9取到最大值为18.所以当点M的横坐标为6时，MN+3PM的长度最大值是18.

二、解后反思

以下主要针对第（2）、（3）问展开反思，我们尝试摆脱上面主要是基于“数”的角度解题的思维风格，意图从“形”的角度更直观地思考问题的结构.

可见，如果对抛物线的焦点、准线知识有所了解，对于数学“念头”或直觉的获得，那一切都只不过是逻辑的必然，情况就像小学的某些奥数应用题用中学的方程来处理一样，知识对解题有指导作用.解题需要居高临下，因为初中数学和高中数学在本质上是相通的，有些初中数学中的所谓难题，需要我们用“高观点”来进行把握.

三、命题导向与教学之思

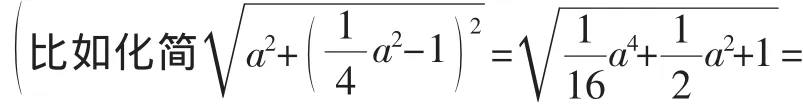
1.罗增儒．数学解题学引论［M］．西安：陕西师范大学出版社，2008.

2.贺信淳．从多角度审视一道中考试题说开去——谈对初中数学教育现状之惑［J］．数学通报，2013（12）.

3.邬吉利．一类“伪坐标系”考题的评析与商榷［J］．中学数学（下），2014（8）．

4.邢成云．中考命题需要谨慎，一石三鸟当思量［J］．中学数学（下），2015（3）．H