多基线组合求解深空航天器载波相位模糊方法

周 欢，李海涛，2，陈少伍，徐得珍，董光亮

(1．北京跟踪与通信技术研究所，北京100094;2．北京航空航天大学电子信息工程学院，北京100191)

0 引言

随着月球和深空探测任务的复杂性进一步增加，地外天体轨道交会对接和采样返回等对导航定位精度要求越来越高。我国嫦娥三号任务取得圆满成功后即将开展探月三期采样返回等工作，火星探测也在规划之中。精确的航天器导航定位不仅可以为任务安全提供保障，也能为科学探测提供更多的支持。现阶段深空航天器导航主要还是依靠地基无线电跟踪测量，传统的测距和多普勒测速方法与无线电干涉测量技术是主要的测量手段［1］。测距和测速可以获得航天器精确的距离和速度信息，干涉测量主要用于测角，确定航天器在天平面上的位置。随着航天器与地球距离的增加，同等测角精度下的定位误差也随之增大，因此需要不断提高无线电干涉测量精度。

无线电干涉测量技术利用互相关的方法求得航天器信号到达两个相距很远的测站的时间差，根据测角几何确定航天器的位置(如图1所示)。时延的测量精度与航天器定位精度息息相关，是该技术的关键之一。受限于航天器下行信号带宽，无线电干涉测量技术由早期的差分甚长基线干涉测量(Delta Very Long Baseline Interferometry，ΔVLBI)发展为现在的双差单程测距(Delta Differential Oneway Range，ΔDOR)［2－4］。ΔDOR技术通过在航天器下行信号中加入几个频率上间隔很远的测距音(DOR音)，求解信号传输的群时延，等效于增大信号带宽，有效提高了时延测量精度。但这种方法对增大信号带宽有一定的上限，例如在X频段，国际电信联盟(International Telecommunication Union，ITU)分配给深空探测的最大信号带宽仅50 MHz［5］。一种提高时延测量精度的方法就是测量载波相时延［6］，如果可以获得X频段的载波相时延值，就等效于拥有8．4 GHz左右的信号带宽。我国嫦娥三号航天器ΔDOR技术群时延测量精度最高达到了0．5 ns［7］，如果可以求解X频段的相时延，时延测量精度可以提高到ps量级。相时延测量面临的主要问题是相位模糊。因为相位的2π周期变化，只能测量［0，2π)内的相位值，无法直接获得总时延对应的总相位，所以要获得相时延首先要求解相位模糊。

图1 无线电干涉测量技术示意图Fig．1 Diagram of radio interferometry

现有的一种求解载波相位模糊的方法是频率综合法［8－9］。该方法在下行干涉测量信标中加入多个频率分布有一定规则的点频信号，首先通过频率间隔小的点频获得群时延粗值，然后利用该初值解除频率间隔更大的点频之间的群时延模糊，获得更精确的群时延，最后利用精确的群时延求解相时延的模糊。日本的月亮女神(SELENE)航天器就是利用特殊设计的频点解出了S频段的相时延，时延测量精度可达几十个ps量级［10］。该技术的不足在于需要航天器发射多个用于解模糊的点频信号，信号设计比较复杂，占用了下行发射功率，容易干扰遥测和科学数据传输。

本文提出利用多基线组合的方法直接求解载波相位模糊。第一节建立了多基线组合求解载波相位模糊的数学模型，根据模型约束推导了基线组合要求。第二节利用美国国家射电天文台(National Radio Astronomy Observatory，NRAO)下属的甚长基线阵(Very Long Baseline Array，VLBA)仿真校验了模型的正确性。第三节根据我国已有的测站资源，分析了在我国深空任务中求解航天器载波相时延的可行性和不足，给出了满足本文方法要求的站址选择建议。

1 多基线组合求解载波相位模糊的数学模型

多基线组合求解载波相位模糊的基本原理为:根据无线电干涉测量的几何关系，测量基线越短，一个相位整周模糊对应的测角误差越大。首先利用全部基线测量的群时延确定航天器先验角位置，如果该先验角位置精度足够高，就可以直接确定短基线的相位整周模糊度，得到短基线的相时延;然后利用多条(至少两条)不平行的短基线相时延值可以有效提高航天器角位置精度，进而求解较长基线的相位模糊。依此类推，基线长短和方向搭配合适的情况下可以解出所有基线的相位模糊，得到精确的航天器角位置。为了简化分析过程，近似认为航天器信号为平行波，只考虑信号到达两个测站的几何时延。

1．1确定航天器先验角位置

航天器在天平面上的先验角位置精度决定了是否可以解出短基线的相位模糊。首先根据可用的测量信标，利用全部基线进行ΔVLBI或ΔDOR测量，通过最小二乘拟合对航天器进行单点定位［11］。单通道群时延测量精度可以用下式估计［12］

式中:Δf为信号带宽，S为信噪比。双通道或多通道情况参考文献［12－13］。结合无线电干涉测量几何原理，基线长度为B时，有

式中:c为光速，τ为信号到达两个测站的几何时延，θ为基线方向与航天器视线方向的夹角(取(0，π/2］)。式(2)两边求导可以得到时延测量误差与测角误差之间的关系为(忽略误差正负)

通过对全部基线进行分析可以为航天器在天平面的先验位置精度提供一个估计。在实际工程测量中，还可以结合测距和多普勒测速数据提供更精确的航天器轨道［7］。用3ε误差椭圆来表示航天器在天平面的二维角位置精度。假设航天器在天平面的先验角位置为Ppre±δPpre，其中Ppre包含了赤经、赤纬两个分量，δPpre包含了定义误差椭圆的长半轴、短半轴和倾角。

1．2求解短基线载波相位模糊

多基线解载波相位模糊需要多条长短方向合适的基线组合，首先建立求解其中单条短基线的相位模糊的数学模型。假设有M个地面测站，可以构成n=条长为Bi(i=1，2，…，n)的基线。不妨令B1＜B2＜… ＜Bn，第i条基线上的总时延为τi，相应的测角为θi。载波频率为f时，该基线总时延引起的总相位差为=2πfτi。设总时延的模型估计值为，对应的相位为，因此经过相关处理过程中时延补偿后的残余相位φRi为

如果能获得总相位差就可以获得精确的相时延。δφi为信噪比的倒数［12］，相比于一个整周模糊度引起的相位误差要小很多。

对于基线Bi，其时延测量值为，利用航天器天平面先验角位置可以反推该基线的几何时延为。假设航天器先验角位置误差在该基线天平面投影方向上的误差分量为(单条基线只能得到一个方向的位置信息)。从式(6)可以看出，由该基线对应的相位整周模糊和测量误差引起。当时延中存在一个相位整周模糊度时，基线Bi的角位置测量偏差将达到λ/(Bisinθi)，λ为载波波长。

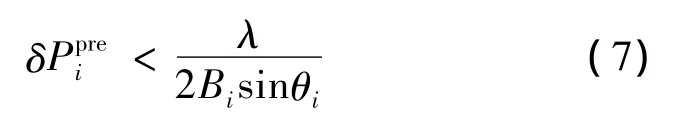
就可求解出相位整周模糊度Ni(如图2所示)

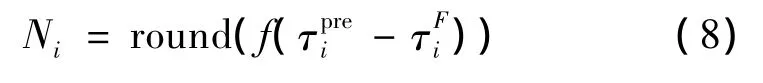
round(·)表示四舍五入取整。此时基线Bi测量得到的精确相时延为

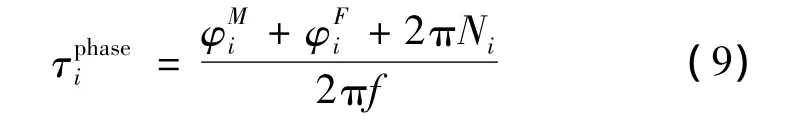
相时延测量精度为

相时延确定的航天器角位置误差为

图2 求解单条基线载波相位模糊示意图Fig．2 Diagram of resolving carrier phase ambiguity on a single baseline

目标位置和载波频率一定的情况下，基线Bi越短越容易满足式(7)，所以先解出短基线的载波相位模糊。上述推导包含了对基线长短的重要约束，即:1)长基线需要尽量长才能利用群时延干涉测量值获得较高精度的航天器角位置先验值;2)短基线必须足够短才能利用先验角位置知识解其载波相位模糊。得到多条不平行的短基线的相时延后，再利用最小二乘拟合求解航天器的角位置，其精度将得到极大的提高。

1．3迭代求解剩余基线相位模糊

利用短基线相时延测量值得到的航天器角位置作为先验信息，可以迭代求解剩余基线的相位模糊。假设已解出基线B1，B2，…，Bi的相位模糊，利用前i条基线相时延值，通过最小二乘拟合可以确定航天器角位置，相应的角位置误差椭圆由各条基线相时延确定的角位置误差决定。当基线B1，B2，…，Bi在各个方向上分布较为均匀时，角位置误差椭圆会得到有效减小，其在基线Bi+1天平面投影方向上的误差分量为，如果满足

就可以根据式(8)求解出基线Bi+1的相位模糊度Ni+1。依此迭代，基站布局合理时可以获得所有基线的相时延。

建立以上模型时没有考虑大气对流层、电离层等扰动，实际应用时需要采用同波束观测或短间隔交替观测射电源进行系统标校，削弱路径上的相位噪声。

2 仿真校验

结合美国VLBA对本文方法进行仿真校验。VLBA包含10个口径25 m的天线，分布在美国本土(如图3所示)，测站间距离由200多千米到8600千米不等［14］，具体的基线长度分布见表1。可以看到几百千米长的短基线数量很多，还拥有多条长基线，基线长度和指向分布比较均匀。美国航空航天局(National Aeronautics and Space Administration，NASA)和NRAO曾利用VLBA开展过一系列航天器相位参考成图试验，其定位精度比美国深空网(Deep Space Network，DSN)的 ΔDOR技术更高，优于1 nrad［15－16］。

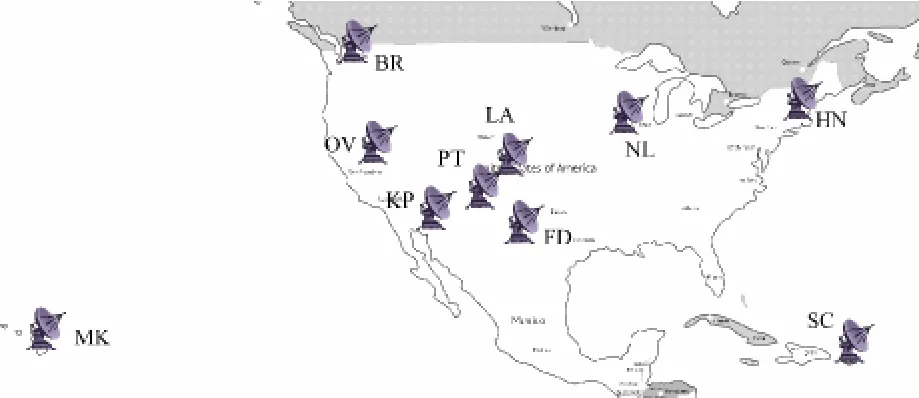
图3 VLBA测站分布图Fig．3 VLBA station configuration

表1 VLBA基线长度表Table 1 Lengths of the baselines of the VLBA

以跟踪土星探测器卡西尼号为背景，假设目标航天器的赤经赤纬分别为西经110度，北纬16度，可以求得航天器信号在每条基线上的精确几何时延。航天器下行信号中心频率设为8．47 GHz，群时延测量精度为0．6 ns，相位测量误差为十分之一个周期。首先在每条基线精确的几何时延上加入－5到5之间随机整数倍的信号周期，再加入幅度为－0．1到0．1倍信号周期的白噪声，模拟精度约为0．6 ns的群时延。然后利用这些基线的群时延确定航天器在天平面上的位置，进行2000次蒙特卡罗试验，得到其测量误差椭圆如图4(a)实线所示。下面求解各条基线的相位模糊。

1)根据式(7)，一共有6条基线满足相位模糊求解约束，分别是FD-PT，FD-KP，LA-PT，LA-KP，LA-OV，PT-KP。可以看到短基线FD-LA虽然只有600多千米，但是因为其天平面投影方向上航天器先验角位置误差分量较大，无法满足求解约束;反而是东西方向上超过1000千米的基线LA-OV解出了相位模糊，这是由于VLBA在该方向上具有长基线，相应的先验角位置精度较高。

2)利用上述6条基线获得的精确相时延值再次求解航天器角位置，其位置误差椭圆如图4(a)点划线所示。相比于全部45条基线群时延，6条基线相时延得到的航天器位置精度得到了很大的提高。

3)利用第2步解出的航天器角位置作为先验信息，可以求得另外9条基线的相位约束，分别是HNNL，HN-BR，NL-LA，NL-OV，NL-BR，FD-LA，FD-OV，PT-OV，KP-OV。综合已解出相位模糊的全部15条基线相时延值对航天器进行定位，得到的误差椭圆如图4(a)点线所示，位置精度得到进一步提高。

4)利用第3步解出的航天器位置可以解出剩余所有基线的相位模糊，最终得到的航天器位置误差椭圆如图4(a)虚线所示，航天器角位置误差小于1 nrad，比群时延测量精度提高了近50倍。

最后对基线的闭合相时延进行统计，图4(b)为SC-HN-NL基线的闭合相位统计直方图示例，可以看到基线的闭合相位基本符合均值为0的正态分布，说明了相时延求解的正确性。需要说明的是，随着目标航天器位置的不同，航天器先验角位置误差椭圆也会随之改变，导致整个解算过程有所不同。上述仿真校验了多基线组合求解载波相位模糊方法的有效性。

图4 基于VLBA的多基线组合解载波相位模糊仿真结果Fig．4 Simulation results of carrier phase ambiguity resolution based on the VLBA

3 多基线组合求解载波相位模糊技术的应用分析

我国正在建设全球深空测控网系统，喀什和佳木斯两个深空站已经投入使用并成功支持了嫦娥三号任务，加上原有的VLBI观测网位于上海佘山和天马、北京、昆明和乌鲁木齐的五个测站，一共有七个大口径天线，布局如图5所示。每个测站都配备了干涉测量数据采集设备，具备开展无线电干涉测量的能力［17］。下面先分析利用七个测站间形成的21条基线解载波相位模糊的可行性。

上述七个测站的基线长度如表2，可以看到我国干涉测量网严重缺乏短基线。以跟踪嫦娥探月任务为背景，目标航天器的赤经赤纬假设为东经110度，北纬30度，其它仿真参数与第3节保持一致。只有佘山至天马的6公里短基线可以满足式(7)的约束条件，但该基线太短以至于即使解出其对应的相时延，也无法有效提高测角精度。因此只依靠我国现有测站，很难利用多基线组合求解X频段的载波相位模糊。

图5 我国深空测站分布图Fig．5 Chinese observation network configuration

与VLBA相比，我国干涉测量网的另一个不足是最长基线不够长，同等群时延测量精度下，航天器先验角位置误差更大，使得短基线必须更短才能满足相位模糊求解要求。如果尝试求解S频段的载波相位模糊，可以使得式(7)更容易满足。为此我们提出一个新建测站的站址选择方案，在我国现有测站布局的条件下，构造合适的短基线求解S频段的载波相位模糊。站址选择依据如下:1)充分利用现有的短基线，并尽量选择低纬度建站，改善对低赤纬目标的跟踪能力;2)兼顾南北和东西两个方向的测角精度;3)满足多基线组合求解载波相位模糊的约束。为此至少需要新建两个测站，一种可行的站址坐标为(120．12°E，33．31°N)和(119．64°E，31．58°N)(图5中黑色方块所示)。第一个测站位于北京到天马基线上靠近天马的三等分点，位于江苏盐城市附近;第二个测站至第一个测站的基线与第二个测站至天马的基线相垂直，位于江苏金坛市附近。由此可以增加多条150至200千米的短基线，而且保证了各个方向的测量精度。

对扩展后的干涉测量网进行仿真。S频段(2．4 GHz)信号带宽窄，时延测量精度相比X频段要低，假设为0．85 ns，相位测量误差为百分之五个周期。利用全部基线群时延解得的航天器角位置先验值可以解出新增的6条最短基线和喀什至乌鲁木齐基线的相位模糊，然后进一步解出另外10条基线的相位模糊，并最终得到所有基线的相时延。整个解算过程中航天器角位置误差椭圆变化如图6(a)，佘山－天马－北京基线的闭合相位统计直方图如图6(b)。可以看到在这种条件下，本文方法顺利地解出了所有基线的相时延，有效地提高了航天器角位置精度。

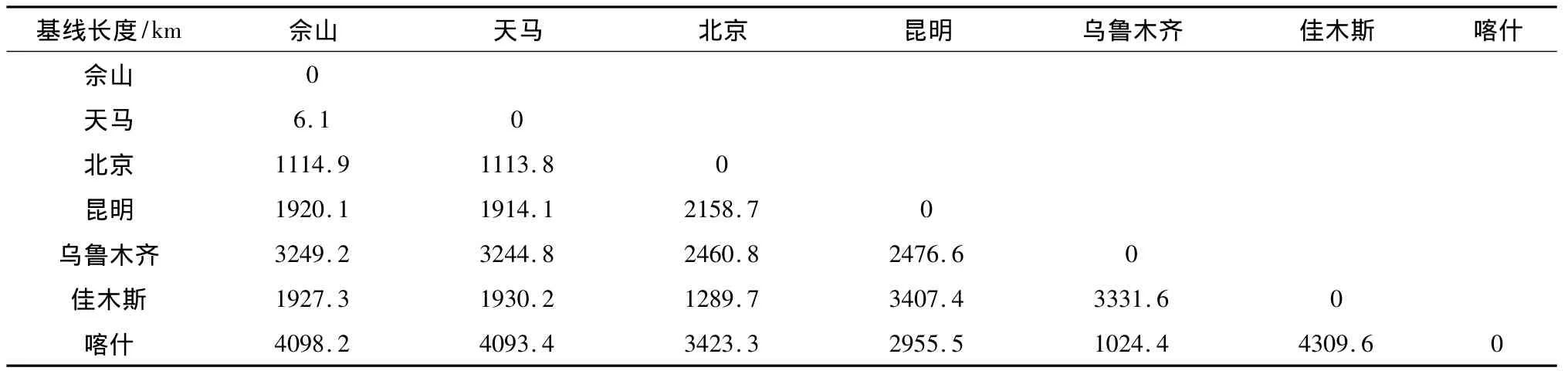
表2 我国干涉测量网基线长度表Table 2 Lengths of the baselines of the Chinese observation network

图6 新增两个测站后基于我国测控网的多基线组合解载波相位模糊仿真结果Fig．6 Simulation results of carrier phase ambiguity resolution based on the Chinese observation network with two new stations

4 结束语

深空导航精度要求越来越高，求解载波相时延可以极大地提高无线电干涉测量精度。本文提出的多基线组合求解载波相位模糊方法可以在现有无线电干涉测量的基础上通过地基基线组合获得精确的相时延。与频率综合法在频域上解模糊的原理不同，多基线组合实际上是在空域上求解信号整周模糊。随着群时延测量精度的提高，航天器先验角位置误差将进一步减小，更有利于满足相位模糊求解约束。未来的一个研究方向是利用我国现有的多个18 m左右口径的测控天线来补充干涉测量网，在系统误差得到良好标校的情况下，有望解出载波相位模糊。

［1］Border JS，Lanyi G E，Shin D K．Radiometric tracking for deep space navigation［C］．The 31st Annual AAS Guidance and Control Conference，Breckenridge，USA，February 1－6，2008．

［2］Curkendall D W，Border J S．Delta-DOR:the one-nanoradian navigation measurement system of the deep space networkhistory，architecture，and componentry［R］．JPL:Interplanetary Network Progress Report 42－193，May 2013．

［3］ 李春来，张洪波，朱新颖．深空探测VLBI技术综述及我国的现状和发展［J］．宇航学报，2010，31(8):1893－1899．［Li Chun-lai，Zhang Hong-bo，Zhu Xin-ying．A survey of VLBI technique for deep space exploration and trend in China current situation and development［J］．Journal of Astronautics，2010，31(8):1893－1899．］

［4］MaddèR，Morley T，AbellóR，et al．Delta-DOR，a new technique for ESA＇s deep space navigation［J］．ESA Bulletin，2006，128:68－74．

［5］Kwok A．Frequency and channel assignments［R］．DSN:DSN Telecommunications Link Design Handbook 810－005，Rev．E，December 2009．

［6］Martin-Mur T J，Highsmith D E．Mars approach navigation using the VLBA［C］．The 21st International Symposium on Space Flight Dynamics，Toulouse，France，September 28－October 2，2009．

［7］Huang Y，Li P J，Chang S Q，et al．Orbit determination of Chang’E-3 and positioning of the lander and the rover［J］．Chinese Science Bulletin，2014，59:3858–3867．

［8］ 陈少伍，董光亮，李海涛，等．同波束干涉测量差分相时延观测模型研究及验证［J］．宇航学报，2013，34(6):788－794．［Chen Shao-wu，Dong Guang-liang，Li Hai-tao，et al．Research and verification of differential phase delay measurement model of same beam interferometry［J］．Journal of Astronautics，2013，34(6):788－794．］

［9］ 陈少伍，刘庆会，董光亮，等．月球轨道器交会对接同波束VLBI测量差分相时延实时解算［J］．中国科学:信息科学，2013，43(11):1460－1471．［Chen Shao-wu，Liu Qing-hui，Dong Guang-liang，et al．Real-Time differential phase delay resolving of same beam VLBI in lunar orbiter rendezvous and docking［J］．Science China:Information Sciences，2013，43(11):1460－1471．］

［10］Kikuchi F，Liu Q，Hanada H，et al．Picosecond accuracy VLBI of the two sub-satellites of SELENE(KAGUYA)using multifrequency and same beam methods［J］．Radio Science，2009，44:1－7．

［11］ 郭丽．基于VLBI跟踪观测的空间飞行器瞬时状态参量归算［D］．上海:中国科学院研究生院(上海天文台)，2007．［Guo Li．Reduction of the instantaneous state vectors of spacecraft based on VLBI tracking data［D］．Shanghai:Shanghai Astronomical Observatory，Chinese Academy of Sciences，2007．］

［12］Takahashi F，Kondo T，Takahashi Y，et al．Very long baseline interferometry［M］．Tokyo:Ohmsha Press，2000．

［13］Whitney A R．Precision geodesy and astrometry via very-longbaseline interferometry［D］．Cambridge:Massachusetts Institute of Technology，1974．

［14］Napier PJ，Bagri D S，Clark B G，et al．The very long baseline array［J］．Proceedings of the IEEE，1994，82(5):658－672．

［15］Lanyi G，Border J，Benson J，et al．Determination of angular separation between spacecraft and quasars with the very long baseline array［R］．JPL:Interplanetary Network Progress Report 42－162，August 2005．

［16］Fomalont E，Martin-Mur T J，Border J S，et al．Spacecraft navigation using the VLBA［C］．The 10th European VLBI Network Symposium and EVNUsers Meeting:VLBIand the New Generation of Radio Arrays，Manchester，UK，September 20－24，2010．

［17］ 钱志瀚，李金岭．甚长基线干涉测量技术在深空探测中的应用［M］．北京:中国科学技术出版社，2012:10－15．