对空间碎片的相对位姿估计

宋 亮，李 志，马兴瑞

(1．中国空间技术研究院钱学森空间技术实验室，北京100094;2．广东省政府，广州510031)

式中:

0 引言

航天技术经过半个多世纪的发展，已逐渐成熟并在人类的生产生活中发挥着愈加重要的作用。但与此同时，频繁的航天活动也造成近地轨道日渐拥挤。美国空间监视网(Space Surveillance Network，SSN)的数据显示，在轨可跟踪空间物体的数量已超过21000个［1］，其中绝大部分为空间碎片。空间碎片，特别是大体积空间碎片占据了稀缺的轨道资源并对在轨航天器构成了极大的威胁。为消除空间碎片带来的碰撞风险，采用服务航天器进行空间碎片清除的研究项目已经提上日程。

对空间碎片执行清除操作的前提是通过相对测量手段获取空间碎片与服务航天器间的相对位置与姿态信息(相对位姿)，基于相对位姿信息进行位姿控制实现对目标的绕飞观测与逼近停靠，进而完成复杂的碎片清除操作。作为一种成熟的视觉测量敏感器，单目相机在相对位姿测量领域得到了广泛的应用［2］。相比于功能更完备但也更复杂的双目相机和激光雷达，单目相机具有技术实现简单、体积质量小、功耗低等优势，在应用上更具灵活性和经济性。

空间碎片的几何、质量参数一般不可知(包括质量、转动惯量、质心、形状和尺寸)，且可能处于姿态翻滚状态，是典型的姿态翻滚未知目标。因此，无法将适用于合作目标的相对位姿估计算法应用在空间碎片上。同时，当空间碎片由于某种原因处于姿态翻滚状态时，其参数的未知性更是对基于单目相机的相对位姿估计算法［3－6］提出了挑战。

在目前的研究中，对于没有任何先验知识的未知目标，单独使用单目相机进行相对位姿估计仍是一个难题。其困难主要在于距离相关量的解算。一些研究通过引入额外信息，使单目相机对未知目标的相对位姿估计成为可能［7－9］。针对单目相机无法直接测距的问题，文献［7］在单目相机测量信息的基础上引入激光测距信息，采用扩展卡尔曼滤波(Extended Kalman Filter，EKF)建立了相对位姿估计算法，解决了对未知目标的相对位姿估计问题。文献［8］使用结构光提供额外的信息，结合相机测量方程，完成了对未知目标局部区域的相对位姿解算。这两种方式的缺点在于增加了系统的复杂性。文献［10］通过对静态目标不同角度成像所得的多幅图像，基于相机的散焦信息进行了相对位姿解算，但该方法难以应用在动态目标上。可见，必须引入额外的信息解决单目相机在距离测量上的不足。此外，当以未知、姿态翻滚的空间碎片作为目标时，对其未知惯量参数的估计也是一项关键技术。文献［11－12］采用不同的模型对该问题进行了研究。

本文针对单独使用单目相机对未知目标进行相对位姿估计的问题，以几何、质量参数未知的空间碎片为目标，基于单目相机获得的目标特征视线测量，在不依赖结构光、无需距离测量敏感器/惯性测量单元辅助且不使用散焦信息的前提下，给出了一种基于EKF的相对位姿估计算法。

1 基本知识

1．1基本假设

在相对位姿估计中涉及两个空间物体，服务航天器和空间碎片。空间碎片作为一个未知目标，其外形、尺寸、质量、质心位置和转动惯量等参数均是未知的，且处于姿态翻滚状态。服务航天器作为主动航天器具有姿态控制与轨道控制能力。服务航天器上装备一部单目相机作为唯一的相对测量敏感器，通过单目相机可以获得目标特征点的视线测量信息。假设目标上具有固定数量的特征，这些目标特征间的相对位置关系对于估计算法而言是未知的。通过对图像特征的识别，相机在对目标成像时可以获得这些特征的像素坐标，即视线测量。通过对目标特征的跟踪，可以进一步得到相同特征在序列图像中的视线测量。图像特征相关技术不在本文研究范围内，其过程将由数学模型模拟。

1．2坐标系定义

相对运动坐标系(Local Vertical/Local Horizontal，LVLH){H}:定义同文献［6］。目标与服务航天器间的相对位置r、相对速度v及相应的运动方程均在此坐标系中表示，qH→I表示该坐标系相对惯性系的姿态。

服务航天器主轴坐标系{A}:坐标系原点位于航天器质心，坐标轴沿惯量主轴方向。相机位置偏置TB在此坐标系中表示，qA→I表示服务航天器的绝对姿态。

目标主轴坐标系{B}:坐标系原点位于目标质心，坐标轴沿惯量主轴方向。目标绝对角速度ωB和目标特征位置ρi(如图1所示)均在此坐标系中表示，qB→I表示目标的绝对姿态。

相机测量坐标系{C}:坐标系原点位于{A}中的TB位置，z轴沿相机视线轴方向，qC→A为该坐标系相对于服务航天器主轴系{A}的姿态。

图1 相对测量几何Fig．1 Relative measurement geometry

1．3相机测量方程

相机的直接测量为目标特征在成像平面上的像素坐标(Xi，Yi)。但如将像素坐标作为滤波器的测量输入，将导致复杂的测量方程和滤波敏感矩阵。因此一般采用与其等价的视线测量形式作为滤波器测量输入。

单目相机测量几何如图1所示。其中，第i个目标特征相对于相机(将相机视为一个点)的位置矢量li可表示为

式中:·表示四元数乘。

由式(1)可得第i个目标特征的视线测量为

式(4)即为本文提出算法的测量输入。下面推导测量协方差矩阵。根据小孔成像模型，第i个特征的视线测量bi与对应的像素坐标(Xi，Yi)间有如下关系

式中:f为相机的焦距。对式(5)求像素坐标(Xi，Yi)的偏导，可得测量误差传递关系如下

式中:

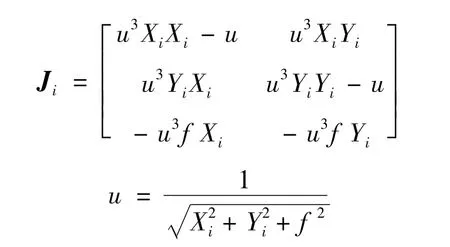
由式(6)可得视线测量bi的协方差矩阵为

2 运动方程

2．1相对位置运动方程

考虑到空间碎片所处轨道的多样性，研究中将采用与文献［6］类似的、适用于非圆轨道的相对位置运动方程。令xt=［rTvT］T，则有相对位置运动方程如下所示

式中:Bt=［03×3I3×3］T/mA为轨控矩阵，mA为服务航天器质量;ut为服务航天器轨道控制量;wt～N(0)是均值为零、方差为的高斯噪声;Γt=［03×3I3×3］T为噪声系数矩阵。ft形式如下

式中:θ为轨道真近点角，rc为轨道半径，pc为半正交弦。绝对轨道参量θ、rc和pc可以通过服务航天器的轨道确定系统较为精确地得到，将作为已知量用于滤波方程中。

2．2姿态运动方程

选择四元数作为姿态参数，建立目标的绝对姿态动力学方程和姿态运动学方程。现有文献对于相对姿态估计问题中滤波状态的选取各有不同。文献［12］选择相对姿态和目标绝对角速度作为滤波状态，但假设服务航天器保持对地定向，即服务航天器的姿态角速度与轨道角速度一致。文献［5］选择相对姿态和相对角速度作为滤波状态，但假设目标的姿态角速度与轨道角速度一致。本研究不对目标和服务航天器的姿态和角速度做任何限制，在采用服务航天器姿态确定系统提供自身绝对姿态的前提下，将目标绝对姿态和绝对角速度作为滤波状态。

目标的姿态运动学方程和动力学方程分别为

式中:IB=diag(Ix，Iy，Iz)为目标的主惯量矩阵;wr～N(0)是均值为零、方差为的高斯噪声;为ωB的叉乘矩阵。由于目标的惯量矩阵是未知的，因此不能直接使用式(11)建立滤波方程。为此，定义惯量比p=［p1p2］T=［Iy/IxIz/Ix］T，用惯量比p替换式(11)中的Ix、Iy和Iz，得到新的姿态动力学方程如下

式中:

惯量比p是常量，因此有

2．3目标特征

将目标特征位置ρi作为估计状态是对未知目标进行相对位姿估计的关键。假设目标为刚体，则特征位置 ρi为常数，所以有。令Π=为目标特征的集合向量，则有

3 滤波器设计

本节将基于EKF方法给出滤波器的具体实现。选取系统状态如下

式中:qv，B→I为目标绝对姿态的矢部，δqv，B→I为qv，B→I的误差形式;δωB为目标绝对角速度的误差形式。δqv，B→I的运动方程为［12］

对式(12)进行变分运算，可得

式中:

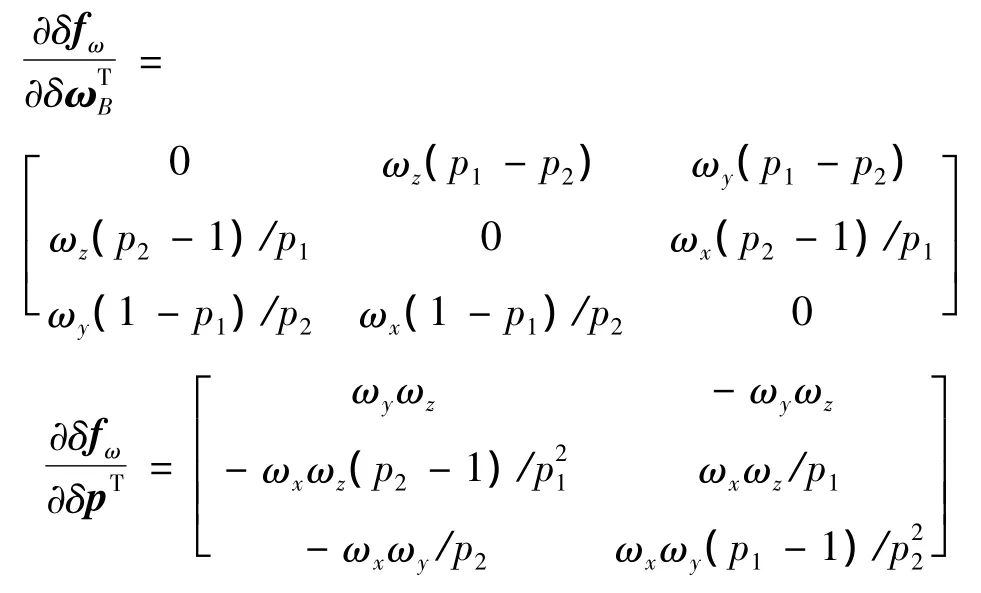
根据式(9)、(13)、(14)、(16)和(17)可得线性化的系统状态方程如下

式中:

由系统矩阵F可得滤波状态转移矩阵的一阶近似Φ=I26×26+FΔt，Δt为滤波周期。由状态转移矩阵Φ可得过程噪声矩阵为

下面将给出滤波测量方程。对于N个特征视线测量{b1，…，bN}，测量方程为

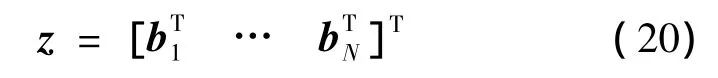
对式(20)求系统状态(15)的偏导，可得滤波敏感矩阵如下

式中:

EKF算法流程可参考文献［6］。

4 算法核心思想

算法基于EKF实现，现对滤波状态的选取进行说明。首先，对于相对位姿估计问题，相对位置/速度、姿态/角速度必须作为滤波状态。而对于未知空间碎片，由于其转动惯量未知，因此需将目标转动惯量以某种形式引入滤波状态，本研究中采用了惯量比形式。此外，由于采用目标特征的视线测量作为滤波测量输入，而对于未知目标，特征位置是未知的，因此必须将目标特征位置作为滤波状态。完整的滤波状态包括了以上讨论的所有物理量。然而，由于单目相机视线测量缺少距离维度信息，如果以上述方式建立滤波算法，则仅能对姿态、姿态角速度和惯量比等姿态相关状态进行有效估计。对相对位置、相对速度和目标特征位置等距离相关状态是不可观。下面给出两个关键条件可以保证新算法对距离相关状态也是可观的，即全部位姿状态均可被有效估计出。

4．1关键条件

条件1．将相机位置偏置TB引入滤波测量方程中。目前，基于滤波方法、采用视觉测量敏感器(不局限于单目相机)进行相对位姿估计研究时，一般假设测量敏感器位于所搭载航天器的质心上，如文献［3，6，12－13］。因此在动力学意义上，即相对位置运动方程中，敏感器和航天器被视为一体。这种建模上的简化会在估计结果中引入系统误差，损失一定的估计精度。文献［5］在建立相对位置运动方程和测量方程时，考虑了相机相对于航天器质心偏置安装的问题，通过引入相机安装位置矢量TB，建立了非质点形式的相对位置运动模型。通过仿真，分析了上述两种建模方式间的差别，并得到非质点形式相对位置运动模型可以给出更好估计结果的结论。这一结论无疑是正确的，但该文作者并没有发掘出其蕴含的更为重要的一个特性。即通过引入相机的位置偏置，结合相对位姿运动的耦合关系，使得仅基于单目相机的视线测量，即可完成对未知目标的相对位姿估计。

条件2．服务航天器进行轨道机动。若不引入相机位置偏置，为了提供额外信息解决位置相关状态的可观性问题，需要服务航天器进行轨道机动。引入服务航天器的轨道机动是有明确物理意义的。轨道机动既可以是使服务航天器对目标进行受迫绕飞的轨道机动，也可以是使服务航天器逼近/远离目标的轨道机动。引入轨道机动是视线导航中解决位置状态可观性问题的常规方法［14］，但视线导航中不考虑姿态，因此本研究中的问题更加复杂。

4．2可观性分析

本节将进行可观性分析证明第4．1节给出条件的作用。首先采用基于Lie导数的可观性秩条件法进行可观性分析，具体方法可参考文献［15］。由于本文建立的滤波器维数大，难以人工写出求解可观性秩过程中涉及到的复杂矩阵。故采用Matlab符号函数工具箱建立可观性分析方程并求解，最终得到可观性矩阵的秩为26，为满秩。因此根据第4．1节提出的两个条件建立的滤波算法是可观的。基于可观性秩条件给出的可观性结果并不能形象说明本文提出的算法是如何有效解决可观性问题的，下面通过解析方法进行可观性分析。

首先需要指出的是，单目相机对未知目标相对姿态的测量是不存在可观性问题的［16］，文献［11］所研究的即为基于单目相机视线测量的姿态/角速度估计问题。因此，下面对可观性的分析仅针对位置相关状态。为方便推导，在分析过程中假设姿态相关状态都是可知的。

本文算法的可观性问题与视线导航中存在的可观性问题非常相似，都是基于单目视线测量进行相对状态估计的可观性问题。事实上，本节给出的可观性分析就是基于Geller和Klein［17］在视线导航领域的研究成果进行的。本节分析采用与文献［17］类似的可观性判定条件:通过对目标特征进行一段时间的测量，根据测量信息，若可以唯一确定一组初始的相对位置、相对速度以及目标特征位置，则算法对位置相关状态是可观的。

首先证明当第4．1节提出的条件不满足时，算法对位置相关状态是不可观的。根据式(4)，对于第i个特征点，其t0时刻的视线测量如下(为方便讨论，将变量在LVLH坐标系中表示)

式中:

不失一般性，以线性形式表示相对位置运动方程，如文献［17］。因此有

式中:

将式(23)代入式(22)中，可以得到以r(t0)、v(t0)、ρi(t0)表示的特征视线测量bi。其中项包含了相机位置偏置表示轨道机动项。若第4．1节提出的条件均不满足，则和均为零，目标特征视线测量可表示为

根据可观性判定条件，若算法是可观的，则通过一系列{bi(t0)，…，bi(tN)}，可以唯一确定一组初值r(t0)、v(t0)、ρi(t0)。但对于式(24)，对于任意正常数 α，αr(t0)、αv(t0)、αρi(t0)同样使式(24)成立，即{bi(t0)，…，bi(tN)}不能唯一确定一组状态初值。因此不满足可观性条件，此时估计算法对位置相关状态不可观。

下面使用文献［17］中的方法证明，当第4．1节提出的条件满足时，估计算法是可观的。假设除r(t0)、v(t0)、ρi(t0)，存在另外一组相对位置、相对速度以及目标特征位置初值可以产生与式(22)相同的视线测量，如下(以相机位置偏置为例进行证明)

为使式(25)成立，必有

式中:

同理，对于ti时刻可得

式中:

将式(27)中的ti分别代之以t1、t2并与式(26)联立，得到如下方程组

式中:

进一步可得

将式(27)中的ti分别代之以t3、t4，并将由式(29)求得的代入，可得如下形式的方程

式中:

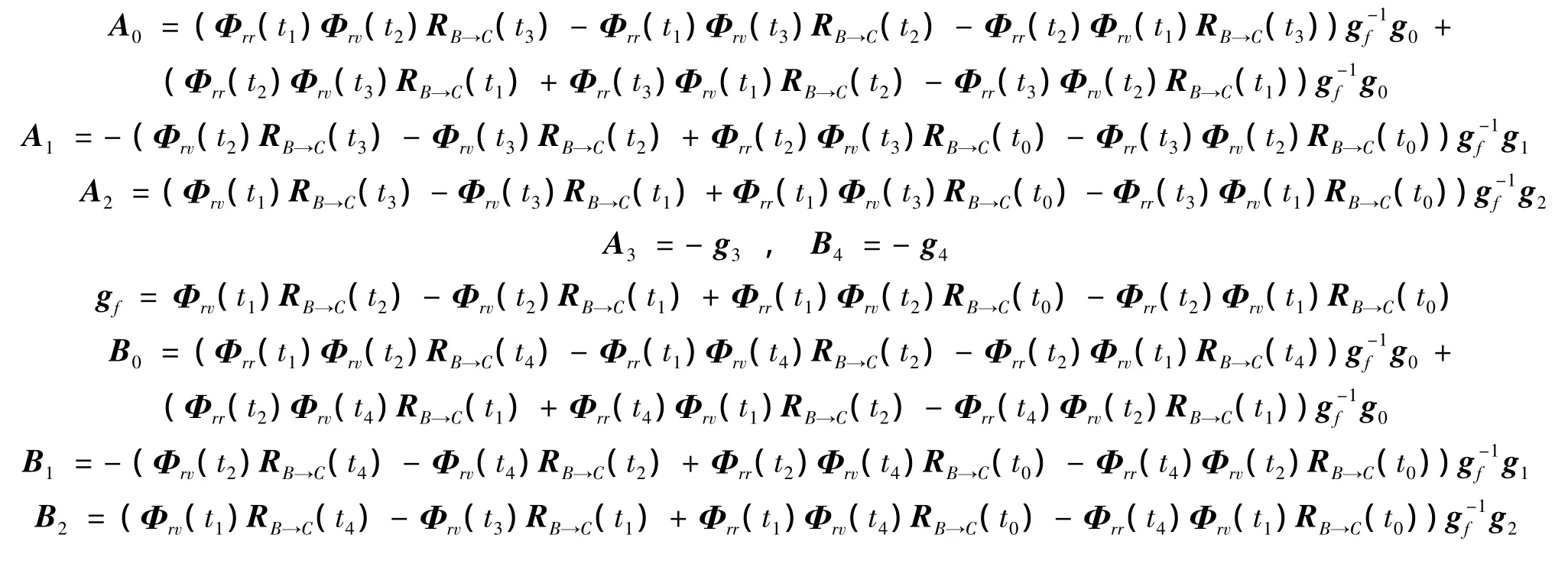
对式(30)、(31)联立方程组，如下

式中:

当TB不为零时，根据Ai和Bi的表达式可知矩阵M是列满秩的。因此式(32)中的K必为零向量。由此证得，通过一系列的测量{bi(t0)…bi(tN)}可以唯一确定相对位置、相对速度和目标特征的初值r(t0)，v(t0)，ρi(t0)，满足可观性判定条件，所以本文提出的估计算法对位置相关状态是可观的。结合姿态相关状态的可观性，可得本文算法对所有状态都是可观的，证毕。

以上可观性分析过程以相机安装位置TB为例，证明了TB对算法可观性的关键作用。轨道机动的作用与相机位置偏置TB完全相同，证明过程相似，不再给出。

5 数值仿真

5．1仿真算例

给出三个仿真算例，分别为相机位置偏置和轨道机动单独作用的情况，以及相机位置偏置和轨道控制均不作用的情况。

算例1．服务航天器对目标进行自然绕飞(相机位置偏置单独作用，无轨道机动)

选择目标轨道参数为，半长轴a=6698455 m，偏心率e=0．05。服务航天器与目标的相对轨道参数为

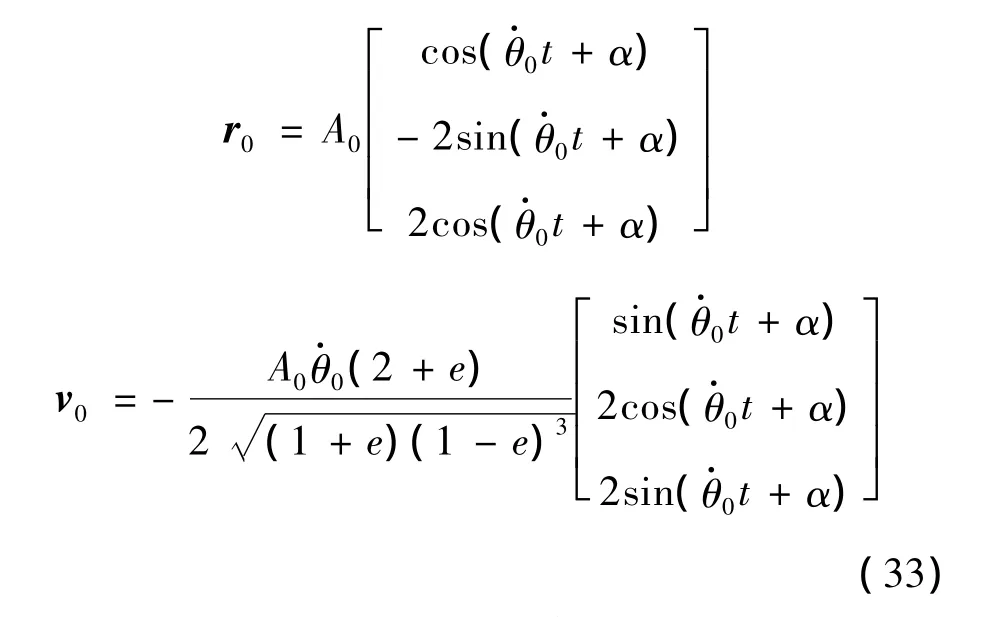
式中:A0=30 m，α=π/4，=0．0012 rad，t=0。相机位置偏置TB=［0．5 0．5－1］Tm。仿真过程中服务航天器不进行轨道机动，但需进行姿态控制保证单目相机的视线方向对准目标。算例2、3中对服务航天器姿态的要求同算例1。

算例2．服务航天器对目标进行受迫绕飞(轨道机动单独作用，相机位置偏置为零)

轨道初始条件同算例1，但将相机位置偏置TB设置为零，即相机与服务航天器质心重合。服务航天器通过轨道控制进行受迫绕飞。为了进行对比，选择与算例1绕飞轨道相近的受迫绕飞轨道。选取方法如下:根据式(33)选取绕飞制导点，取t=600i，i=1，…，10，其他参数同算例1，获得10个制导点。由这10个制导点组成的绕飞轨道与算例1中的自然绕飞轨道形状相似，但周期不同。

算例3．服务航天器对目标进行自然绕飞(相机位置偏置为零且无轨道机动)

轨道初始条件同算例1，但将相机位置偏置TB设置为零，且无轨道控制。

以上三个算例中，目标均处于姿态翻滚、无控状态。目标的姿态参数初值为

在滤波器中，状态相关的测量协方差矩阵根据式(7)计算。初始协方差估计为P0=diag(I3×3，I3×3，2I2×2，500I3×3，I3×3，25I12×12)，在滤波器中设置初始状态估计值为仿真值的150%。目标特征位置(目标主轴系{B}中表示)设置如表1所示。

表1 目标特征位置Table 1 Feature locations

5．2仿真结果与分析

受篇幅所限，仅将算例1的全部仿真结果列出。图2～图7给出算例1全部状态估计结果(姿态以欧拉角的形式给出)，所有结果均以误差形式给出，即估计值与真值之差(图中实线)，并且同时给出相应的3σ误差界(图中虚线)。图7给出一个特征位置的估计结果，其他特征位置估计的收敛趋势具有相似性，不逐一给出。仿真结果显示，误差界可以较为准确地描述估计偏差，所有估计状态均得到较为准确的估计。因此当条件1满足时，算法有效。算例2的结果与算例1相似，不再给出。

图2 姿态估计误差曲线与误差界(3σ)Fig．2 Estimated errors for the target＇s attitude and 3σbounds

图3 角速度估计误差曲线与误差界(3σ)Fig．3 Estimated errors for the target＇s angular velocity and 3σbounds

图4 惯量比估计误差曲线与误差界(3σ)Fig．4 Estimated errors for the inertia ratios and 3σbounds

算例3中所有姿态相关状态均收敛且收敛趋势与算例1、2相似，说明算例3条件下的算法对姿态是可以有效估计的。但是算例3中的算法无法对位置相关状态进行有效估计，所有位置相关状态均不收敛。

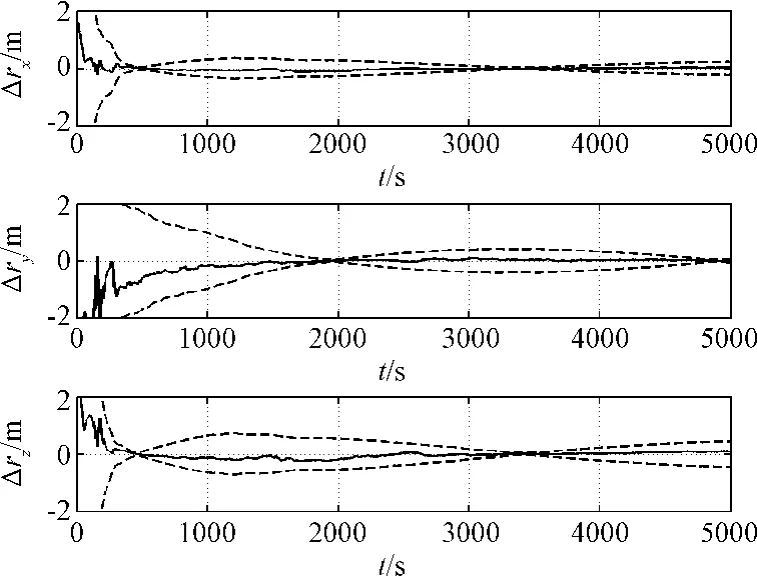
图5 相对位置估计误差曲线与误差界(3σ)Fig．5 Estimated errors for relative position and 3σbounds

图6 相对速度估计误差曲线与误差界(3σ)Fig．6 Estimated errors for relative velocity and 3σbounds

图7 特征位置估计误差曲线与误差界(3σ)Fig．7 Estimated errors for the feature locations and 3σbounds

由仿真结果可得，相机位置偏置(算例1)和服务航天器的轨道机动(算例2)均能保证滤波状态的完全可观。如果没有这两者之一，单目相机仅能对姿态相关状态进行有效估计，对距离相关状态不可观。

6 结论

本文基于单目相机视线测量，采用EKF建立了针对未知空间碎片的相对位姿估计算法。提出了两个可以保证算法可观性的关键条件，并通过可观性分析进行了证明。最后对三个典型算例进行了数值仿真，校验了算法的有效性。

［1］National Aeronautics and Space Administration．Space debris and human spacecraft［EB/OL］．2013［2014］．http://www．nasa．gov/mission_pages/station/news/orbital_debris．html#．VCzdNnExjBg．

［2］Florian S，Toralf B，Jörn S，et al．On－orbit servicing missions:challenges and solutions for spacecraft operations［C］．SpaceOps 2010 Conference，Huntsville，Alabama，April 25－30，2010．

［3］Zhang L，Yang H，Zhang S，et al．Kalman filtering for relative spacecraft attitude and position estimation:a revisit［J］．Journal of Guidance，Control，and Dynamics，2014，37(5):1706－1711．

［4］Xing Y，Cao X，Zhang S，et al．Relative position and attitude estimation for satellite formation with coupled translational and rotational dynamics［J］．Acta Astronautica，2010，67(3):455－467．

［5］ 邢艳军，曹喜滨，张世杰，等．非质心特征点相对位置和姿态估计方法研究［J］．宇航学报，2010，31(9):2129－2137．［Xing Yan－jun，Cao Xi－bin，Zhang Shi－jie，et al．Relative position and attitude estimation of feature point deviating from center of mass［J］．Journal of Astronautics，2010，31(9):2129－2137．］

［6］Kim S，Crassidis J L，Cheng Y，et al．Kalman filtering for relative spacecraft attitude and position estimation［J］．Journal of Guidance，Control，and Dynamics，2007，30(1):133－143．

［7］Padial J，Hammond M，Augenstein S，et al．Tumbling target reconstruction and pose estimation through fusion of monocular vision and sparse－pattern range data［C］．2012 IEEE Conference on Multisensor Fusion and Integration for Intelligent Systems，Hamburg，Germany，September 13－15，2012．

［8］ 高学海，梁斌，潘乐，等．非合作大目标位姿测量的线结构光视觉方法［J］．宇航学报，2012，33(6):728－735．［Gao Xue－hai，Liang Bin，Pan Le，et al．Pose measurement of large non－cooperative target using line structured light vision［J］．Journal of Astronautics，2012，33(6):728－735．］

［9］Augenstein S，Rock SM．Improved frame－to－frame pose tracking during vision－only SLAM/SFM with a tumbling target［C］．2011 IEEE International Conference on Robotics and Automation，Shanghai，China，May 9－13，2011．

［10］Kuhl A，Wöhler C，Krüger L，et al．Monocular 3D scene reconstruction at absolute scales by combination of geometric and real－aperture methods［C］．Pattern Recognition，Berlin，Germany，September 12－14，2006．

［11］ 王峰，陈雪芹，曹喜滨．在轨服务航天器对失控航天器参数估计算法研究［J］．宇航学报，2009，30(4):1396－1403．［Wang Feng，Chen Xue－qin，Cao Xi－bin．The research of onorbit parameters estimation for on－orbit－servicing spacecraft relative to out－of－control spacecraft［J］．Journal of Astronautics，2009，30(4):1396－1403．］

［12］Aghili F，Parsa K．Motion and parameter estimation of space objects using laser－vision data［J］．Journal of Guidance，Control，and Dynamics，2009，32(2):538－550．

［13］Segal S，Carmi A，Gurfil P．Vision－based relative state estimation of non－cooperative spacecraft under modeling uncertainty［C］．IEEE Aerospace Conference，Big Sky，USA，March 5－12，2011．

［14］Woffinden D C，Geller D K．Observability criteria for anglesonly navigation［J］．Aerospace and Electronic Systems，IEEE Transactions on，2009，45(3):1194－1208．

［15］ 宋亮．星敏感器陀螺姿态确定系统在轨标定研究［D］．哈尔滨:哈尔滨工业大学，2011．［Song Liang．Research on on－orbit calibration methods for star tracker－gyro attitude determination system［D］．Harbin:Harbin Institute of Technology，2011．］

［16］Hartley R，Zisserman A．Multiple view geometry in computer vision［M］．2nd Edition．Cambridge:Cambridge University Press，2003．

［17］Geller D K，Klein I．Angles－only navigation state observability during orbital proximity operations［J］．Journal of Guidance，Control，and Dynamics，2014，37(6):1976－1983．