混合推进最省燃料轨道设计方法

张 晨，赵育善

(北京航空航天大学宇航学院，北京100191)

0 引言

在深空探测任务中，探测器使用的发动机可分为化学发动机和电推进发动机两大类。化学发动机产生的推力大但耗费燃料。电推进发动机因其高比冲的特性能够极大地节省燃料消耗，但其相对较小的推力幅值导致较长的任务时间。Mingotti等［1］提出的混合推进方式能够兼容以上两种发动机各自的优点，这种方法假定卫星上面级提供一次脉冲后与卫星分离，之后卫星携带的电推进发动机开机并最终进入目标轨道。混合推进方式相比单纯使用化学发动机，能够大幅降低燃料消耗，还有操控灵活，对发射窗口不敏感等优点;且相比单纯使用电推进发动机，混合推进方式提供了更短的任务时间。

近十多年来，国内外对电推进轨道优化技术进行了丰富的研究。任远等使用混合法设计了地火电推进转移轨道［2］，避免直接求解两点边值问题，从而提高了迭代的收敛性。Jiang等［3］研究了同伦方法以及开关检测技术在最省燃料问题当中的应用，并获得了很高的收敛效率和打靶精度。Guo等［4］将同伦方法和粒子群算法结合起来研究了引力辅助在电推进轨道优化方面的应用，获得了更高的剩余燃料比。黄镐等［5］将协态归一化方法和曲线拟合技术相结合，研究了最优电推进逃逸轨道设计问题，降低了多圈问题协态初值猜测的敏感性。上述研究探索了二体模型下的电推进轨道设计方法，近些年来针对深空探测任务提出的新需求，基于三体以及四体模型的电推进轨道设计问题在国内外得到了越来越多的关注。Ozimek等［6］研究了使用变比冲发动机的三体电推进轨道优化问题，基于数值方面的考虑，其推力和比冲没有设定上下限。Caillau等［7］基于庞特里亚金极大值原理和同伦方法，探讨了三体模型下使用定比冲发动机的最省燃料问题，为降低求解复杂度，固定初始发射轨道为地球静止轨道。Russell［8］使用帕累托最优探索了多目标优化下的三体电推进问题，舍弃了一个打靶约束用于提高收敛性。而到目前为止探讨混合推进方式轨道设计方法的研究还较少。Mingotti等［1］将电推进技术和多体引力场下的弹道捕获技术相结合，研究了混合推进方式捕获轨道的设计方法，但其所采用的方法并未将两种发动机的燃料消耗总和进行统一优化。

本文探讨了地－月圆型限制性三体模型下混合推进方式的最省燃料轨道设计问题。将两种发动机的燃料消耗总和作为目标函数统一进行优化，并推导了一阶必要条件，此外还在Russell［8］工作的基础上，进一步推导了最省能量问题的状态转移矩阵。上述方法被用于设计从近地圆轨道出发，到达地－月L1附近Halo轨道的混合推进转移轨道。仿真结果表明，通过设定初始发射脉冲为优化变量，可以进一步节省燃料消耗，并且飞行时间和最终剩余燃料不同的组合方式增加了任务设计的灵活性，而上述改进提高了同伦方法的鲁棒性和计算效率。

1 圆型限制性三体问题

限制性三体问题是在两个大天体P1和P2共同旋转坐标系中研究质量可忽略不计的小天体P3的运动;如果两个大天体绕其公共质心做圆周运动则称为圆型限制性三体问题(Circular Restricted Three-Body Problem，CRTBP)。在地－月CRTBP下，P1代表地球，P2为月球，定义其质量分别为m1和m2，设定两个天体之间的距离、总质量以及旋转角速率都为1，系统的质量参数定义为μ=m2/(m1+m2)。容易验证地球的质量为1－μ并位于(－μ，0，0)，而月球的质量为μ并位于(1－μ，0，0)。卫星P3在地－月引力场和电推进发动机共同作用下的动力学方程表示如下［8］:

式中:Tmax是最大推力幅值，u∈［0，1］为发动机推力幅值比，α是推力方向的单位矢量，c2=Isp2g0代表电推进发动机燃气速度，(Isp2是电推进发动机比冲，g0是海平面重力加速度)，定义g(r)和h(v)为旋转坐标系下位置与速度的函数，其具体表达式为［8］

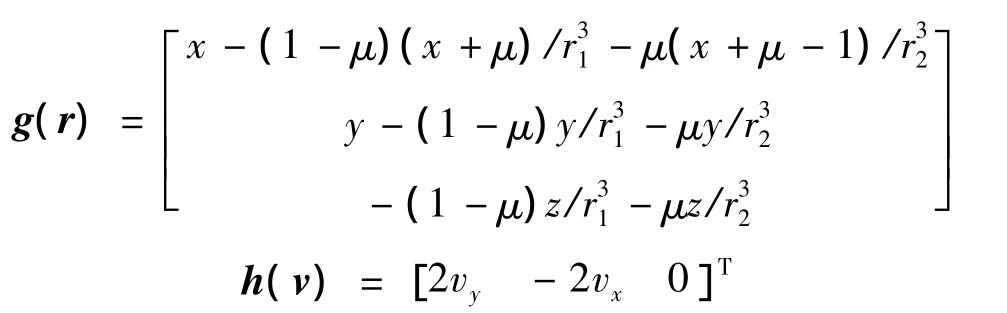
r1和r2分别代表卫星到地球和月球的距离，表示为

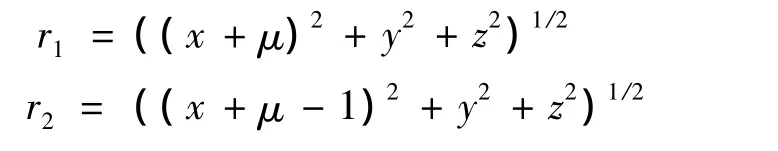
2 混合推进轨道优化问题

假设卫星初始位于近地圆轨道，卫星上面级提供一次脉冲后电推进发动机开机，则混合推进方式最省燃料问题的性能指标可表示为

式(2)等号右端第一项和第二项分别代表化学推进发动机和电推进发动机的燃料消耗质量(需要注意的是，式(2)使用归一化的质量单位，即脉冲前系统质量为单位1)。Δv为脉冲所产生的速度改变量。c1为化学推进发动机燃气速度。t0和tf分别代表任务初始和最终时刻。对于最省燃料问题，推力幅值在任何时刻只能为输出最大推力或者关机两种状态(不考虑奇异情况)，这种“bang-bang”性质使得动力学方程不连续并导致打靶过程非常敏感［3］。Bertrand等［9］使用一种平滑技术即同伦方法来改善收敛性。通过引入同伦参数ε，定义新的性能指标为

当ε=1时式(3)代表最省能量问题，当ε=0时式(3)表示最省燃料问题。

如图1所示，假设卫星初始位于地心距为r0的圆轨道上。卫星上面级提供一次脉冲后电推进发动机开机，则施加脉冲后卫星在地－月旋转系下的状态x0可由两个参数κ和θ确定，如下所示

图1 混合推进方式的转移轨道示意图Fig．1 Hybrid transfer trajectory illustration

式中:κ∈［1，1．4］表示初始脉冲比，即施加脉冲后，卫星速度介于停泊轨道速度与地球逃逸速度之间。而θ∈［0，2π］表示脉冲发射相位角。此外式(4)中脉冲Δv可表示为κ的函数，即

卫星上面级施加脉冲后电推进发动机开机，电推进转移轨道需要满足的初始状态约束表示为

可以发现当给定参数κ和θ时，式(5)的约束自然满足，即x(t0)=x0(κ，θ)。假设卫星在tf时刻到达地－月系L1附近Halo轨道上固定的一点，且剩余质量m(tf)自由，电推进转移轨道需要满足的终端状态约束为

为方便讨论，定义式(3)中化学发动机燃料消耗质量为Θ。对于边界约束，引入拉格朗日乘子υ0和，有约束的最优控制问题就被转换成了无约束的最优控制问题，新的目标函数J1表示如下

假设飞行时间tf固定，J1取得极值的必要条件是其一阶变分等于0，即

通过式(9)可推导协态变量的动力学方程为［8］

梯度矩阵G=∂g(r)/∂r，H=∂h(v)/∂v。此外从式(9)还能得到如下关系

式(11)也称为横截条件，由于 λ0，λf，υ0，υf均为未知的拉格朗日乘子，式(11)只表明如果终端时刻的质量m(tf)自由，则其所对应的协态变量应等于0，即λm(tf)=0。此外，由式(9)还能得到由于κ和θ自由而产生的两个约束条件

庞特里亚金极大值原理(Pontryagin Maximum Principle，PMP)揭示了控制变量应在整个时间历程上都使得哈密顿函数取极小值，则最优推力方向为

式中:S代表开关函数

推力幅值比u介于［0，1］之间，为使哈密顿函数H取极小值，需再次使用PMP。观察式(14)可知H是u的二次函数，两个根分别为u1=0以及u2=(ε－S)/ε，此外该二次函数开口向上。根据u2所在区间不同，最优推力幅值比u*一共有三种情况。由于u2=(ε－S)/ε，可进一步得到开关函数S和最优推力幅值比u*的关系(见式(16)和图2)。需说明的是，对最省燃料问题(即±ε=0)，u*的选取只和开关函数S的符号有关，即当S为正时u*=0，而当S为负时u*=1。

图2 最优推力幅值比u*根据开关函数S位置的不同具有三种情况Fig．2 Optimal thrust magnitude ratio u*with respect to the time-varying S

为方便讨论，将状态和协态变量合并为正则变量即y=［xT，λT］T，并将状态方程(1)和协态方程(10)合并在一起称为正则方程，表示为

至此，混合推进轨道优化问题被转换成两点边值问题。当给定t0时刻9个未知的打靶变量［λT0，κ，θ］T，通过积分隐含 α*和u*的式(17)就能够得到终端时刻tf的状态和协态变量。而所选择的9个打靶变量需使得9个打靶等式约束得到满足，与之对应的打靶函数Z如式(18)所示。

一旦求解了最省能量问题(即ε=1)，从1到0逐步降低同伦参数 ε，并将当前步骤所得到的打靶变量作为初值带入到下一步中，最终能够得到所

对应最省燃料问题的解。需注意的是，为避免无穷转移时间问题，需要将飞行时间固定，而最省时间问题给出了飞行时间的下限(即tf≥tfmin)，所以最省时间问题应先于最省能量和最省燃料问题进行求解。对于最省时间问题除了增加一个打靶变量tf之外，还需再增加一个打靶约束，即哈密顿函数在tf时刻的值H(tf)等于0。由于篇幅所限，最省时间问题的一阶必要条件在此不再进行推导。

3 解析雅克比矩阵

如前所述，最优控制问题被转换成两点边值问题并通过打靶法进行求解，但与打靶法相关的牛顿法对于初始点的选取非常敏感。在本文中，为提高牛顿法的鲁棒性和收敛速度，解析的雅克比矩阵被用于提供打靶过程的梯度信息。状态转移矩阵(State Transition Matrix，STM)反映了正则变量y在t0时刻的扰动对t时刻所产生的影响。定义STM为Φ，其性质如下

1)在一个积分步长内如果发动机始终处于开机或者关机状态(即u*为标量)，则表示为［8］

2)当在一个积分步长内发动机推力幅值始终处于中等推力时，由于u*是m，λv以及 λm的函数，参见式(15)和式(16)，通过链式法则可得

式中:

需注意的是，上述状态转移矩阵只对动力学方程连续的正则变量进行映射，即发动机始终保持开机、中等推力或者关机。然而如果推力幅值u*在积分步长内发生切换，则需考虑切换点tj处的状态转移矩阵 ψ(tj)［8］:

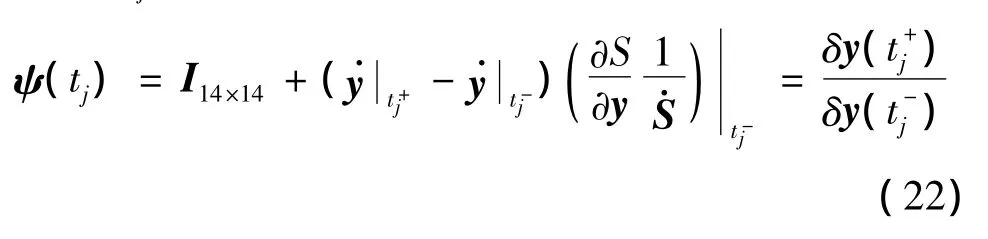
至此，式(23)中的状态转移矩阵Φ(tf，ti)就可用于构造9个打靶等式约束相对于9个打靶变量的雅可比矩阵，表示如下(参见式(18))

4 仿真和结果

假设卫星初始位于近地点高度为400 km的圆轨道，卫星上面级施加一次脉冲Δv后，电推进发动机开始工作并不断提升卫星能量，最终卫星在tf时刻与地－月L1点附近Halo轨道上的一个固定点重合。表1给出了本文所用到的参数，其中长度、时间、速度以及质量都进行了归一化处理。

表1 物理常量及含义Table 1 Simulation parameters

首先求解最省时间问题以确定飞行时间下限。假设卫星上面级提供一次固定大小的脉冲，求解到达L1附近Halo轨道的电推进最省时间转移轨道，其仿真结果如表2所示。当κ=1时代表卫星上面级不提供初始脉冲而只依靠电推进发动机提供动力，整个任务耗时22．6467天，最终剩余质量比为0．7783，其转移轨道如图3所示。随着脉冲比κ从1逐渐增加到1．4，任务时间从22．6467天缩短到了3．3692天，最终剩余质量从0．7783降低到0．3200。当 κ等于1．4时，卫星被施加了一个近似等于地球逃逸速度的脉冲，其转移轨道如图4所示。

表2 发射脉冲固定的电推进最省时间问题收敛解Table 2 Simulation results of minimum-time problem with fixed initial impulse and electronic propulsion

图3 初始发射脉冲为零(即κ=1，θ=－2)的最省时间电推进转移轨道Fig．3 Minimum-time low-thrust trajectory with initial impulse equal to zero(i．e．，κ=1，θ=－2)

图4 初始发射脉冲约为地球逃逸速度(即κ=1．4，θ=－2)的最省时间电推进转移轨道Fig．4 Minimum-time low-thrust trajectory with high initial impulse(i．e．，κ=1．4，θ=－2)

在得到不同κ对应的最短转移时间tfmin之后，可进一步求解混合推进方式的最省能量和最省燃料问题。需说明的是，打靶过程中κ和θ的选取非常敏感，可先将其固定，找到收敛解后再将其依次设定为优化变量。此外为避免“无穷转移时间”问题，可通过引入标量ctf来固定飞行时间，即tf=ctftfmin。

表3 混合推进方式最省燃料问题部分收敛解Table 3 Minimum-fuel solutions with hybrid propulsion system

表3列出了混合推进方式的部分收敛解，其中tf为飞行时间，mf为最终剩余质量。通过设定κ和θ为优化变量，mf得到了不同程度的提高。下面选取一组收敛解对比转移轨道和电推进发动机的控制曲线。

1)固定 κ=1．24、θ=－2、飞行时间比ctf=1．2，此时在CRTBP下最省燃料转移轨道如图5所示。其中粗实线代表电推进发动机推进段，细实线代表无动力滑行段，虚线代表Halo轨道。可以发现电推进发动机在近地点附近开机，并在远地点处关机用于节省燃料消耗。

图5 地－月旋转系下固定发射脉冲的最省燃料转移轨道(κ=1．24，θ=－2且c tf=1．2)Fig．5 Minimum-fuel low-thrust trajectory in CRTBP with fixed initial impulse(κ=1．24，θ=－2 and c tf=1．2)

图6为推力幅值比和开关函数随时间变化的曲线，推力幅值呈现“bang-bang”控制结构。通过计算可知，哈密顿函数在整个时间历程上都近似为常值，其最大误差在10－10以内，从而证明了解的精确性。

图6 固定发射脉冲时推力幅值比u和开关函数S随时间变化曲线(κ=1．24，θ=－2且c tf=1．2)Fig．6 When the initial impulse is fixed，the time history of throttle factor u and switching function S(κ=1．24，θ=－2 and c tf=1．2)

2)设定κ和θ为优化变量，飞行时间比ctf=1．2，混合推进方式的转移轨道在地－月旋转系下的仿真图如图7所示。通过和图5对比发现，采用混合推进方式的卫星在初始时刻施加了一个相对较小的初始脉冲，但在近地空间内保持连续开机以提升轨道能量。此外还需要说明的是，接近目标周期轨道的无动力滑行段非常逼近从周期轨道上出发的一条稳定流形，即说明最优轨道能够自动沿着稳定流型运动以节省燃料。之所以在Halo轨道附近仍需施加一段推力弧段，是因为终端约束为Halo轨道上的一个固定点，如果最终不施加推力弧段，则卫星沿着稳定流形需要无穷长的时间才能最终进入Halo轨道，而在固定转移时间的前提下，卫星只能先沿着近似稳定流形的转移轨道逼近以节省燃料，最后发动机开机并最终进入Halo轨道。

图7 地－月旋转系下初始发射脉冲自由的最省燃料转移轨道(κ和θ自由且c tf=1．2)Fig．7 Minimum-fuel low-thrust trajectory in CRTBP with free initial impulse(freeκandθ，c tf=1．2)

电推进发动机的推力幅值比和开关函数随时间变化的曲线如图8所示，可以发现设定κ和θ为优化变量之后，卫星在任务时间的两端保持开机，而只在仿真时间的中间部分关机。

图8 初始发射脉冲自由时推力幅值比u和开关函数S随时间变化曲线(κ和θ自由且c tf=1．2)Fig．8 When the initial impulse is free，the time history of throttle factor u and switching function S(freeκandθ，c tf=1．2)

5 结论

本文基于混合推进方式探讨了地－月圆型限制性三体模型下最优转移轨道的设计问题。根据变分法推导了最优解的一阶必要条件。针对复杂动力学模型下多圈转移轨道带来的打靶迭代速度慢和分段连续的推力幅值导致打靶难以收敛的问题，在前人工作基础上，给出了最省能量问题解析的状态转移矩阵。上述方法被用于求解从近地圆轨道出发，到达地－月L1附近Halo轨道的混合推进转移轨道。数值仿真表明，上述方法可以将化学发动机和电推进发动机的燃料消耗总和进行优化。此外由于给出了燃料消耗以及飞行时间不同的组合方式，混合推进方式使任务设计具有更大的灵活性。

［1］Mingotti G，Topputo F，Bernelli Z F．Earth–Mars transfers with ballistic escape and low-thrust capture［J］．Celestial Mech．and Dyna．Astro．2011，110(2):169－188．

［2］ 任远，崔平远，栾恩杰．利用混合法进行地球－火星电推进轨道设计［J］．哈尔滨工业大学学报，2007，39(3):359－362．［Ren Yuan，Cui Ping-yuan，Luan En-jie．An Earth-Mars low-thrust trajectory design based on hybrid method［J］．Journal of Harbin Institude of Technology，2007，39(3):359－362．］

［3］Jiang F H，Baoyin H X，Li J F．Practical techniques for lowthrust trajectory optimization with homotopic approach［J］．J．of Guid．Con．and Dyna．2012，35(1):245–258．

［4］Guo T D，Jiang F H，Baoyin H X，et al．Fuel optimal low thrust rendezvous with outer planets via gravity assist［J］．Sci．China Phy．Mech．and Astro．2011，54(4):756－769．

［5］ 黄镐，韩潮．基于间接法的最优电推进逃逸轨道设计［J］．中国空间科学技术，2013，33(2):25－31．［Huang Hao，Han Chao．Indirect optimization of low thrust escape trajectories［J］．Chinese Space Sci．and Tech．2013，33(2):25－31．］

［6］Ozimek M，Howell K．Low-thrust transfers in the Earth-Moon system，including applications to libration point orbits［J］．J．of Guid．Con．and Dyna．2010，33(2):533–549．

［7］Caillau J，Daoud B，Gergaud J．Minimum fuel control of the planar circular restricted three-body problem［J］．Celestial Mech．and Dyn．Astro．2012，114(1－2):137–150．

［8］Russell R．Primer vector theory applied to global low-thrust trade studies［J］．J．of Guid．Con．and Dyna．2007，30(2):460–472．

［9］Bertrand R，Epenoy R．New smoothing techniques for solving bang–bang optimal control problems numerical results and statistical interpretation［J］．Optimal Control Applications and Methods，2002，23(4):171–197．

［10］Lawden．Optimal trajectories for space navigation［M］．London UK:Butterworths，1963．