含扩张状态观测器的高超声速飞行器动态面姿态控制

刘晓东，黄万伟，禹春梅，3

(1．北京航天自动控制研究所，北京100854;2．宇航智能控制技术国家级重点实验室，北京100854;3．国防科技大学航天科学与工程学院，长沙410072)

0 引言

与一般飞行器相比，高超声速飞行器面临更复杂的非线性问题、高不确定性问题以及通道强耦合问题等［1］，这样传统的线性控制方法将很难满足高超声速飞行器姿态控制系统的性能需求，最终会导致飞行任务的失败。特别地，对于BTT飞行器，其面临更严重的通道间耦合问题，故通道分离式姿态控制设计方法将会对控制效果和飞行稳定性造成严重的影响［2］。因此，为了改善高超声速飞行器的飞行品质，探索具有强鲁棒性能的非线性、全通道姿态控制技术是非常有必要的。

自抗扰控制技术(Active Disturbance Rejection Control，ADRC)［3］是一种可以实时估计并补偿系统内部不确定动态的控制技术，该控制技术不需要精确的模型信息，也不需要假设不确定模型为参数线性化或有界，因此它可以应对较大范围的不确定系统。在飞行器控制领域，自抗扰控制方法已得到了广泛的应用［4－5］，并展示出传统控制方法无可比拟的效果。实际上，自抗扰控制的强鲁棒性能主要得利于扩张状态观测器(Extended State Observer，ESO)的引入，它可以较为精准地估计出系统当前的未知不确定动态，并将其补偿到控制系统中，而补偿之后的控制系统结构简单易于进一步的设计。综合考虑估计精准性、控制平滑性以及算法简易性，本文将构建一种多变量线性ESO，用于改善高超声速飞行器姿态控制系统的鲁棒性能。而对于引入ESO补偿之后的控制系统，本文将采用动态逆控制理论［6］来完成最终控制律的设计。

另外，高超声速飞行器姿态控制系统的设计模型通常具有控制矩阵不可逆以及非匹配不确定问题，若直接针对该模型进行姿态控制律的设计，则会大大增加设计难度，甚至不易实现。若通过模型分块的方式保证每个子系统的控制矩阵都是可逆的，那么可以采用反演法与多鲁棒面控制相结合的方法进行控制律的设计。该方法不仅可以简化非线性控制系统的设计过程，而且还可以有效应对系统的非匹配不确定问题，因此它已被广泛应用于飞行器姿态控制系统的研究中［7］。但是，传统的积分型反演方法中的连续微分会带来所谓的“计算爆炸”问题，为了解决此问题，Swaroop等人在文献［8］中提出了一种动态面控制(Dynamic Surface Control，DSC)方法。该方法通过引入若干组低通滤波器避免了对虚拟指令的直接微分，具有较高的工程实用价值，因此开始得到国内外学者的广泛关注，并将其应用于飞行器的制导控制设计中［9－10］。然而，目前该技术在高超声速飞行器姿态控制中的研究尚处于初级阶段，关于其全通道动态面姿态控制方法的研究也不多。于是，本文将动态面控制理论引入到高超声速飞行器全通道姿态控制系统的设计中。

本文其余部分的安排如下。第一部分，建立了高超声速飞行器姿态运动方程组，并给出一个面向姿态控制的非线性设计模型。第二部分，提出一种基于多变量ESO的动态逆控制方法，并利用动态面控制理论，完成了高超声速飞行器全通道姿态控制律的设计。第三部分展示了计算机仿真结果，相关的结论和后续工作将在第四部分中给出。

1 问题描述

基于如下假设条件:忽略地球自转的影响;将地球视为均质圆球，不考虑地球扁率的影响;惯性积为小量，忽略其影响。于是，对于面对称的高超声速飞行器，其无动力飞行的姿态运动方程组可以表述为:

式中:α、β、γc分别为飞行器的攻角、侧滑角和速度倾斜角，m、V、θ分别为飞行器的质量、速度和弹道倾角，ωx1、ωy1、ωz1为机体轴角速率，Jx1、Jy1、Jz1为飞行器的主转动惯量为等效干扰力，为等效干扰力矩。此外，Y、Z分别为气动升力和侧向力，Mx1、My1和Mz1分别为滚转力矩、偏航力矩和俯仰力矩，气动表达式如下:

式中:q、S、L分别表示动压、参考面积和参考长度。而且，实际的气动系数是关于飞行器飞行状态的非线性函数。

此时，若选取系统状态向量为x1=［α β γcωx1ωy1ωz1］T，控制向量为u=［δxδyδz］T，则根据式(1)～(2)可以得到如下的状态空间方程:

式中:控制矩阵g(x)∈R6×3是奇异的，ζ∈R6表示非匹配不确定性向量。注意，因为本文不关心式(3)的具体形式，故此处未将其给出。显然，若直接针对模型(3)进行姿态控制律的设计，则会大大增加设计的难度，甚至不易实现。

为了更好地实现高超声速飞行器的姿态控制，可以将式(2)中的各气动系数在某个特征点附近拟合为如下形式:

式中:δx、δy、δz分别表示副翼、方向舵和升降舵的偏角;CYd、CZd、Cx1d、Cy1d、Cz1d表示气动拟合误差项。而且，式中拟合函数可选为线性或非线性函数，需要根据实际情况决定。

根据式(1)～(4)，可得到高超声速飞行器面向姿态控制设计的状态空间模型:

式中:分系统的状态向量为x1=［α β γc］T和x2=［ωx1ωy1ωz1］T，ζ1和 ζ2表示建模误差、参数摄动和外界干扰等系统不确定性，而且

因为数学模型(5)具有严格反馈形式，因此在基于该模型进行姿控系统设计时，不仅可以简化设计过程，而且还可以有效应对姿态控制系统的非匹配不确定问题。

2 高超声速飞行器姿态控制设计

2．1基于ESO的动态逆控制技术

对于多变量非线性系统:

实际工程中，系统的一部分动态是可知的，则式(6)可以改写为如下的形式:

式中:F0(x)和G0(x)表示已知动态，Fn(x)和Gn(x)表示未知动态，并假设G0(x)是非奇异的。于是，需要扩展的状态向量为:

针对式(7)～(8)，我们可以设计如下的多变量线性ESO，用于系统不确定动态的估计:

式中:向量z1是对系统(7)状态向量x的估计，向量z2是对不确定性向量的估计，且β0＞0，β1＞0。

下面首先给出两个引理。

引理1．［11］对于n阶实对称矩阵F，有:

式中:σ－(·)和(·)分别表示矩阵的最小特征值和最大特征值。

引理2．［12］若η＞0，则有:

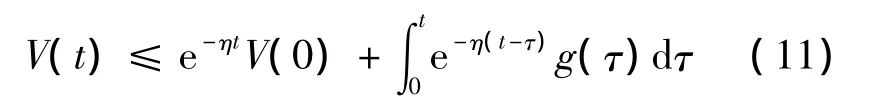
将不确定动态的估计补偿到原系统(6)中，并利用动态逆控制理论，可以得到如下的定理。

定理1．假设ESO对系统不确定动态的估计误差是有界的且有，则针对非线性系统(7)可以设计如下的动态逆控制律:

式中:W是正定矩阵。于是，非线性系统(7)各状态变量的跟踪误差将收敛至邻域内。

证．选取Lyapunov函数如下:

等式两边分别对时间进行求导，可得:

式中:W=2W1，故W1也是正定矩阵。

根据引理1，得到如下的不等式:

同时，根据Cauchy－Schwarz不等式［12］，可得:

基于式(15)～(16)，可以得到如下不等式:

然后，根据引理2，可进一步得到:

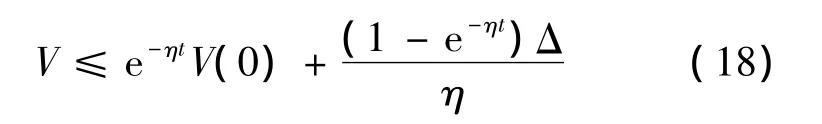
再根据式(13)，可得到如下等式:

因此，当t→∞ 时，有如下的不等式:

根据向量2范数的定义可以得到，非线性系统(7)各状态变量的跟踪误差将收敛至邻域范围内。

由定理1可以看出，在ESO估计误差已定的情况下，增大σ－(W)可以有效减小状态的跟踪误差。

2．2动态面姿态控制律设计

对于形如式(5)的非线性系统，通常采取反演与多鲁棒面控制相结合的方法。但是，传统的反演方法中连续微分会带来“计算爆炸”现象。为了避免此现象的发生，可以采用动态面控制方法［8］，该方法通过引入若干个低通滤波器避免了对虚拟指令的直接微分，故具有较高的工程实用价值。

首先，给出三个基本假设条件，作为下一步姿态控制律设计时的依据［13］。

假设1．高超声速飞行器姿态控制系统中的不确定性向量ζ1和ζ2是范数有界的。

假设3．高超声速飞行器面向姿态控制设计的状态空间模型中控制矩阵g1(x1)和g2(x2)均为非奇异且范数有界的。

然后，构造两个多变量ESO，分别用于估计两个分系统的未知不确定动态，其表达式如下:

式中:系数 β10、β11、β20和 β21均为正数。

最后，基于已经构造出的ESO，可以设计动态面姿态控制律如下:

式中:η=diag(η1，η2，η3)为滤波器系数矩阵，且η1＞0，η2＞0，η3＞0。显然，当x2c→x2d时，控制律(23)便退化为传统的反演模式。

3 仿真结果

本部分将对比本文控制方案与基于传统动态逆的动态面控制方案的仿真结果，并分析本文控制方案的优势。飞行器模型如文献［13］所示，动态面姿态控制方案的参数值如下:

在本文控制方案中，引入了两个多变量ESO进行未知不确定动态的估计，其参数值如下:

对于飞行器机体参数考虑10%的不确定性，对于气动参数则考虑20%的不确定性。此外，在仿真系统中加入时变等效干扰力和等效干扰力矩的影响，如下:

图1 两种控制方案下姿态角跟踪曲线(N T=1)Fig．1 Tracking curves of attitude angles under the two control scheme(N T=1)

图2 两种控制方案下姿态角跟踪曲线(N T=－1)Fig．2 Tracking curves of attitude angles under the two control scheme(N T=－1)

假设攻角、侧滑角和速度倾侧角初始时刻均在零位置，且其跟踪指令分别为5°+1°sin(2πt)、10°+2°sin(2πt)和15°+3°sin(2πt)的复合信号。考虑到实际情况要求，将各舵偏角限制在±30°之间。

仿真中，考虑不确定性系数N［13］T分别为上、下界的两种情况，并给出两种控制方案下姿态角跟踪曲线，如图1～图2所示。通过图1～图2可以看出，相比基于传统动态逆的动态面控制方案，本文控制方案下飞行器的姿态调节速度快、稳态精度高，而且具备针对系统不确定性的较强鲁棒性，故而实现了飞行器姿态控制的目的。

此外，计算机仿真结果表明，在两种仿真情况下，解算的控制量中无明显的高频抖动现象(除一处由于指令切换造成的跳变外)，因此增强了本文控制方案的工程应用性。

4 结论

本文针对高超声速飞行器非线性对象，提出的基于ESO的动态面姿态控制方案，可保证飞行器姿控系统在三通道耦合和系统不确定性的影响下仍具有较好的跟踪性能。仿真结果表明，相比基于传统动态逆的动态面控制方案，本文控制方案下飞行器的动态性能更好，稳态精度更高，姿态控制系统的鲁棒性也更强。而且，本文控制方案结构较为简单，易于工程实现。关于控制律中姿态角指令的微分项，本文直接通过差分法获得，虽然该方法简单实用，但是其抵抗噪声的能力较弱，因此还需要采用一些更为有效的微分方法，如近似微分法或微分跟踪器等。关于此部分的研究将在今后的工作中给出。

［1］ 张天翼，周军，郭建国．高超声速飞行器鲁棒自适应控制律设计［J］．宇航学报，2013，34(3):384－388．［Zhang Tianyi，Zhou Jun，Guo Jian-guo．A study on robust adaptive control method for hypersonic vehicle［J］．Journal of Astronautics，2013，34(3):384－388．］

［2］ 张颖昕，董朝阳，王青等．BTT导弹的协调式分散鲁棒H∞控制器设计［J］．宇航学报，2011，32(4):734－740．［Zhang Ying-xin，Dong Chao-yang，Wang Qing，et al．Decentralized robust H∞controller design for BTT missile with coordinate loop［J］．Journal of Astronautics，2011，32(4):734－740．］

［3］ 韩京清．自抗扰控制技术:估计补偿不确定因素的控制技术［M］．北京:国防工业出版社，2008．

［4］ 秦昌茂，齐乃明，朱凯．高超声速飞行器自抗扰姿态控制器设计［J］．系统工程与电子技术，2011，33(7):1607－1610．［Qin Chang-mao，Qi Nai-ming，Zhu Kai．Active disturbance rejection attitude control design for hypersonic vehicle［J］．Systems Engineering and Electronics，2011，33(7):1607－1610．］

［5］ 齐乃明，秦昌茂，宋志国．高超声速飞行器改进自抗扰串级解耦控制器设计［J］．哈尔滨工业大学学报，2011，43(11):33－38．［Qi Nai-ming，Qin Chang-mao，Song Zhi-guo．Improved ADRC cascade decoupling controller design of hypersonic vehicle［J］．Journal of Harbin Institute of Technology，2011，43(11):33－38．］

［6］Slotine J，Li W．Applied nonlinear control［M］．New Jersey:Prentice-Hall，1991．

［7］Sonneveldt L，Chu Q P，Mulder J A．Nonlinear flight control design using constrained adaptive backstepping［J］．Journal of Guidance，Control，and Dynamics，2007，30(2):322－336．

［8］Swaroop D，Hedrick J K，Yip P P，et al．Dynamic surface control for a class of nonlinear systems［J］．IEEE Transactions on Automatic Control，2000，45(10):1893-1899．

［9］Hou M Z，Liang X L，Duan G R．Adaptive block dynamic surface control for integrated missile guidance and autopilot［J］．Chinese Journal of Aeronautics，2013，26(3):741－750．

［10］Zhang J M，Li Q，Cheng N，et al．Adaptive dynamic surface control for unmanned aerial vehicles based on attractive manifolds［J］．Journal of Guidance，Control，and Dynamics，2013，36(6):1776－1783．

［11］ 黄琳．系统与控制理论中的线性代数［M］．北京:科学出版社，1984．

［12］Ioannou PA，Sun J．Robust adaptive control［M］．Upper Saddle River，New Jersey:Prentice-Hall，1996．

［13］Liu X D，Zhang Y，Wang S，et al．Backstepping attitude control for hypersonic gliding vehicle based on a robust dynamic inversion approach［J］．Proc IMechE Part I:Journal of Systems and Control Engineering，2014，228(8):543－552．