谐波力矩测量技术分析和优化设计

王雪竹，崔 龙，李洪谊，王越超，李 涛，张 涛

(1．中国科学院沈阳自动化研究所机器人学国家重点实验室，沈阳110016;2．中国科学院大学，北京100049)

0 引言

谐波齿轮传动具有重量轻、体积小、传动比大、承载能力大、传动精度高、回差小、能在密封空间和辐射介质的工况下正常工作等优点，因此成为轻型空间机械臂的首选减速装置［1－3］。为提高机械臂的力感知和力控制能力，以及通过力矩反馈控制克服谐波传动系统固有的柔性、啮合过程中的动态误差和复杂的摩擦特性，获得更优的伺服精度［4－8］，需要对谐波传动输出力矩进行测量。常用的力矩测量方法是基于电阻应变原理，在谐波传动和负载之间加入一个弹性体，通过测量该弹性体形变来衡量谐波输出力矩的大小［8－9］。然而在航天航空领域中，由于其独特的工况条件，对机械传动机构的体积、重量、动力特性和可靠性有着严格的要求，额外的力矩传感器增加了零部件数量，使得系统结构更复杂，重量和体积均增大，且弹性体的存在进一步加大了系统柔性。

为克服这一缺陷，考虑到谐波柔轮本身的弹性特性，研究人员提出了谐波测力技术(也称为谐波内置力矩传感器技术)，该技术不需要在谐波传动和负载之间增加新的机械构件，而是将可变形的柔轮当作力矩传感器的弹性体部分，通过测量柔轮形变得到谐波输出力矩值［10］，从而达到节省关节空间和降低关节质量的目的，因而更适合太空应用。由于柔轮除了受负载影响产生形变之外，还在波发生器的作用下产生依赖于其转动位置的形变，这给从测得的柔轮形变信号中提取负载力矩带来很大干扰。因此谐波测力技术的研究重点是抑制测量信号中受波发生器作用产生的柔轮形变部分。Taghirad等将该部分柔轮形变看作正弦信号，采用四个对称分布的应变花并使用惠斯通电桥以抵消该波动信号［11］。Godler等假设该部分柔轮形变为N个频率分量的叠加，采用直角应变花削弱波动信号，并使用增益调节方法抵消由应变片安装误差带来的额外干扰［12］。Pan等采用了类似的增益调节方法对波动信号进行双重补偿［13］。Sensinger等采用四个应变花进行力矩测量，综合使用电桥和增益调节技术将小范围(5 N范围内)的测量误差削减至±0．5 Nm［14］。目前的测量精度不能满足高精度力矩测量的需求，这是因为目前对谐波测力技术的研究缺乏对柔轮复杂的形变过程的分析，仅基于经验对传感器的应变片进行布局，而精确的传感器布局恰恰是抑制波动信号、减小力矩测量误差的关键。

为了提高谐波力矩测量的精度，针对上述问题，本文首先从理论上分析了柔轮形变对谐波测力技术测量精度的影响，然后采用有限元方法对谐波传动依次进行稳态和瞬态动力学分析，得到柔轮在负载作用下的实时应变情况，进而对谐波测力技术的设计方案进行对比分析，得出最优方案。

1 谐波测力技术

谐波测力系统的构成如图1所示，柔轮应变由贴在柔轮表面的应变片转化为电阻变化量，再经电桥转化为电压信号，通过信号处理提取出其中的负载力矩信号，并进行信号采集。谐波传动由刚轮、柔轮和波发生器构成，当波发生器转动时，它与柔轮的接触关系迫使柔轮不断改变形状，柔轮外齿依次啮入和啮出刚轮的内齿，实现啮合过程，完成力与运动的传递。谐波测力技术通过测量柔轮形变得到负载力矩，然而柔轮形变除了受负载力矩影响外，还受波发生器形状、转速以及轮齿啮合过程中的摩擦粘滞效应等因素的影响。摩擦效应主要体现在改变柔轮外齿附近的受力分布，对距离外齿较远部分的影响不大，而且基本不改变柔轮平均形变，因而不妨忽略。波发生器转动给力矩测量带来的干扰很大，下面具体分析如何通过信号处理去除其干扰。

图1 谐波测力系统结构图Fig．1 System organization of the build-in torque sensor for harmonic drive

忽略摩擦效应，柔轮表面某一点的应变量ε可以表示为

式中:εf为由波发生器转动带来的柔轮形变，以下称之为柔轮自身形变，kττload为负载力矩带来的柔轮形变，其中τload为负载力矩，kτ为弹性系数，其大小与该点在柔轮上的位置有关，并受转速影响。可以看出，若能测得柔轮应变量并抵消掉柔轮自身形变，则可测得负载力矩。

采用直角应变花测量柔轮上某一点的应变，如图2(a)所示。对直角应变花建立局部坐标系，直角应变花的两个应变片R1和R2位于xy平面，并关于y轴对称。当受到应力时，应变花产生应变ε=(εx，εy，εz)，如图2(b)所示，其中线段op表示无变形时的应变花，op*表示变形后的应变花。则两个应变片的阻值变化量ΔR1和ΔR2分别为

式中:kx、ky和kz分别为应变片在x、y、z三个方向的灵敏系数，ΔRtemp为温度漂移。

从式(2)可以看出，使用惠斯通电桥对直角应变花的两个应变片进行半桥互补可以去除温度漂移，并得到单方向的应变量εx:

式中:kv为电桥系数。

图2 直角应变花的局部坐标系示意图Fig．2 Local coordinate system of the right-angle strain rosette

为了测量负载力矩，需要将直角应变花沿柔轮上负载力矩的作用方向进行布局。如图3所示，对柔轮建立圆柱全局坐标系(ρ，φ，h)，将N个直角应变花沿h轴对称均匀贴在柔轮表面，间距为Δφ=2π/N，图3(a)为贴在柔轮底部的方案，图3(b)为贴在柔轮筒壁的方案，图中粗线oipi代表第i个应变花，oi－xiyizi为第i个应变花的局部坐标系。不管哪种方案，负载转矩都是沿着图中虚线圆的切线方向，给各个应变花带来其局部坐标系下x方向的应变。因此根据式(1)可得第i个直角应变花在xi方向的应变εxi为

式中:εfxi为柔轮自身形变在xi方向的分量，kτxi为柔轮在第i个应变花处的弹性系数在xi方向的分量。

图3 直角应变花在柔轮上的布局图Fig．3 Layout of the strain rosette on the flexspline

对于常用的双波谐波传动，波发生器为椭圆形对称结构，波发生器每转一圈柔轮转过2个齿，因此柔轮的变化以半圈为一个周期。而波发生器转动过程中柔轮上任一点的形变近似正弦变化，故εfxi可用如下正弦信号的叠加表示:

式中:βi为第i个应变花对应的波发生器转角，bk为第k个正弦分量的幅值。由于应变花的间距为2π/N，故有 βi=β+2π(i－1)/N，其中β=β1，将其代入式(5)可得

将式(4)代入式(3)可得第i个直角应变花的电压输出信号为

将式(6)代入式(7)，使用信号调理电路对N个直角应变花的电压输出信号求均值可得

然而实际中应变花的数目N不可能无穷大，要提高谐波测力的精度，就需要对应变片布局进行分析和改进，使柔轮自身形变对测量值的影响尽量小，即尽量小。另外，由于柔轮形变和负载力矩并不完全呈线性，且柔轮形变在一定程度上受波发生器转速的影响，因此在优化应变片布局时还需要考虑使负载力矩和波发生器转速对弹性系数 的影响尽量小。

2 柔轮动应变分析

根据以上分析可知，为了对谐波测力技术的传感器布局进行分析，需要首先对柔轮在负载作用下的实时应力应变进行分析。由于谐波传动的啮合过程相当复杂，目前对柔轮的理论分析都是忽略了齿圈部分，将柔轮简化为光滑的柱形壳体来计算，其计算结果只是一定程度上的近似，更精确的结果需要采用有限元方法计算得到。

谐波测力技术需要获取转动过程中柔轮的实时应变，因此要进行动态分析。由于装配好的谐波传动在空载时存在预应力，因此在进行动态分析之前还需要对柔轮的初始形变进行静态分析。LS-DYNA显式求解器能快速求解瞬时大变形动力学和复杂的接触碰撞问题，而ANSYS隐式求解方法在处理静态问题时更为有效，因此我们结合这两种方法的优点执行隐式－显式顺序求解:首先使用ANSYS隐式求解波发生器装入后柔轮在空载时的静应变，再将隐式求解结果作为ANSYS/LS-DYNA显式求解的预载进行瞬态分析。

对谐波传动建立有限元模型如图4所示。不妨假设波发生器在转动过程中不发生变形，从而将椭圆盘状的波发生器简化为一个刚性的椭圆环。对柔轮的建模采用未变形的圆筒形，并将柔轮和波发生器两者的中心同轴装配。柔轮的直径为80 mm，筒高42 mm，厚0．6 mm，齿数为160，采用渐开线齿廓。为简化分析，略去柔轮筒底法兰盘上的螺孔，在谐波传动输出端添加一个环形负载圈，以便于施加负载力矩和约束柔轮运动。在仿真中将刚轮假设为不可变形的刚性体，因此刚轮外圈厚度不影响仿真结果，为减少网格数目画得较薄。柔轮的材料为30CrMnSi，其弹性模量为204 GPa，泊松比0．29，密度6．691 g．cm－3，负载圈材料设置同柔轮。波发生器和刚轮的材料为45号钢，其弹性模量为210 GPa，泊松比0．3，密度7．85 g·cm－3。使用八节点实体单元进行网格划分。

图4 谐波传动有限元模型Fig．4 Finite element model of the harmonic drive

使用ANSYS有限元分析软件进行空载时的隐式静态仿真，仿真结果如图5所示，可以看出，空载时柔轮在波发生器和刚轮的共同约束下产生形变，在长轴(x方向)和短轴(y方向)处形变较大，在两者中部形变较小(MN);最大应变(MX)发生在齿圈上，从齿圈到筒壁再到底部应变呈逐渐减小趋势，越靠近柔轮输出端应变越小。

图5 空载时仿真结果Fig．5 Simulation results of the harmonic drive under no-load

将隐式静态仿真的结果作为瞬态分析的预载，导入ANSYS/LS-DYNA软件中，进行显式瞬态分析，分别在转速恒定、负载力矩变化和负载力矩恒定、转速变化的情况下仿真。图6为负载力矩45 Nm、波发生器转速100 rad/s的仿真结果，图(a)和图(b)分别为波发生器逆时针转动0．5 rad和1 rad时的柔轮应变，二者对比可以看出在同样负载下柔轮应变相似，且柔轮的扭曲随着波发生器的转动而转动。对比图5(c)和图6，可以看出柔轮在负载力矩影响下产生明显扭曲，且越靠近柔轮输出端扭曲越明显，即柔轮输出端附近的应变受负载力矩的影响更大;而从图5(b)和(c)中可以看出柔轮输出端附近柔轮自身形变的干扰更小，因此初步认为靠近柔轮输出端的地方更适合安装应变片。接下来使用仿真得到的柔轮实时应变对应变片布局进行定量分析。

图6 负载下柔轮应变仿真结果Fig．6 Simulation results of the flexspline strain under loads

3 传感器优化设计

使用第2部分的谐波传动有限元计算结果来分析不同方案下的力矩测量效果。首先从有限元计算结果中获取直角应变花的应变:如图3所示，将第i个直角应变花简化为由柔轮表面的点oi和pi构成的长为l的线段，将有限元仿真得到的点pi的实时应变转换到局部坐标系oi－xiyizi下，则可以得到直角应变花oipi在局部坐标系下的应变。

对各个直角应变花在其局部坐标系下x方向的应变量εxi求均值，由式(8)可得

式中:j为采样时间，n为采样长度，τest(j)=kest(j)为力矩测量值，其中kest为对和τload最小二乘拟合的结果，计算方法为kest=，其中Tload=［τload(1)… τload(n)］T。

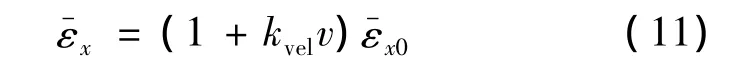
在谐波传动系统转动过程中，柔轮表面不同位置的应变受柔轮自身形变、负载力矩和波发生器转速的影响并不相同，而应变片的大小也影响测量值，因此以下分别对应变片位置ρ或h、应变片长度l和数目N对力矩测量精度的影响进行分析。

1)空载时的应变量

空载时，根据有限元仿真结果，按图3(a)所示在柔轮底部布置直角应变花，应变花数目N=178，长度l=2 mm，则不同半径ρ下应变花可测得的应变如图7(a)所示;按图3(b)所示在柔轮筒壁布置直角应变花，N=178，l=2．4 mm，则不同高度h下应变花可测得的应变如图7(b)所示。图中φ=0°和180°为波发生器长轴对应的位置。可以看出柔轮应变以半圈为一个周期，空载时柔轮底部应变较小，且越靠近柔轮输出端形变越小;柔轮筒壁应变很大，且不同高度下应变大小差别不大。这表明柔轮自身形变对柔轮筒壁的测量值影响较大，而对柔轮底部靠近输出端的测量值影响较小。

2)应变片位置、长度与力矩测量误差的关系

图7 空载下直角应变花的应变Fig．7 Strains of the strain rosette on the flexspline under no-load

施加负载，波发生器的转速为100 rad/s，负载为0～45Nm，仿真时间为0．01 s。在柔轮筒壁布置直角应变花，N=178，l=2．4 mm，使用式(10)求不同高度h下的均方根误差σ，结果如图8所示。可以看出σ的范围为3．5～13．6 Nm，且与高度的关系并不明确。该谐波传动的正常工作范围为±50 Nm，故误差为谐波量程的3．5%～13．6%。图9为误差最小处(h=17．4 mm)的力矩测量曲线，实线为负载力矩，虚线为力矩测量值，可以看出测量值未能很好地跟随真实值变化，测量误差偏大。原因是筒壁的形变受齿轮啮合影响较大，齿轮啮入啮出会带来应变尖峰，产生噪声，而且负载力矩对柔轮筒壁形变的影响相对柔轮自身形变而言较小。因此筒壁不适合用来贴应变片。

在同样负载下，在柔轮底部布置直角应变花，N=178，l=2 mm，使用式(10)求不同半径ρ下的均方根误差σ，结果如图10中细实线所示。可以看出，σ范围为1．28～2．64 Nm，且随着ρ的减小呈递减趋势。这是因为筒底的形变受柔轮自身形变影响相对较小，且越靠近负载输出地方，受负载力矩影响越大，这和图6、图7(a)的结论也是相符的。

依次改变应变花的长度l为4 mm、6 mm、8 mm、10 mm和12 mm，使用式(10)求得均方根误差σ如图10中对应曲线所示。可以看出，长度对测

图8 筒壁上不同高度处的力矩拟合误差σFig．8 Torque measurement errors for different positions on the tube of the flexspline

图9 筒壁上误差最小处的力矩测量曲线Fig．9 The best torque measurement on the tube of the flexspline

3)弹性系数与转速的关系

图10 筒底上不同半径处的力矩拟合误差σFig．10 Torque measurement errors for different positions on the bottom of the flexspline

图11 筒底上误差最小处的力矩测量曲线Fig．11 The best torque measurement on the bottom of the flexspline

图12 筒底上不同半径处速度对弹性系数的影响系数Fig．12 Effect of the velocity on elasticity on the bottom of the flexspline

4)应变片数目与力矩测量误差的关系

在波发生器转速为100 rad/s、负载为0～45 Nm下仿真，时长0．01 s，选取如下应变片设计方案进行分析:ρ=31．6 mm，l=4 mm。改变应变花个数N，使用式(10)求不同N下的均方根误差σ，结果如图13所示。可看出，当N＜14时，随应变花个数的增加，力矩测量误差迅速降低，σ由5．5 Nm降至2 Nm以内;当N较大，尤其是N＞30时，力矩测量误差随应变花个数的变化较小，此时σ在1．3～1．8 Nm之间波动，但总体上仍呈下降趋势。

图13 不同应变花个数下的力矩拟合误差Fig．13 Torque measurement errors for different numbers of the strain rosette

综合以上分析，可以得出如下结论:(1)柔轮筒壁形变受柔轮自身形变影响较大，故力矩测量误差较大;(2)柔轮底部形变能够较好地反映负载力矩，且越靠近输出轴测量误差越小;(3)适当增加应变花长度有利于减小测量误差;(4)选择筒底中部位置并适当增加应变片长度可以减小转速的影响;(5)力矩测量误差随着应变花个数的增加而递减，应变花个数较少时下降较快，应变花个数较多时变化不大。

为提高测量精度，期望速度对弹性系数的影响尽可能小，且力矩测量误差σ低于2%，即2 Nm。故选择将直角应变花贴在柔轮底部ρ=31．6 mm处，应变片长度l=4 mm。考虑到实际应用中应变片数目过多会增加布片难度，根据图13选择应变花数目为误差σ下降变慢的转折点N=14，此时均方根误差σ=1．6 Nm。无滤波时的力矩测量曲线如图14中虚线所示，曲线的波动主要是由齿轮的啮入啮出带来的。加上低通滤波器0．5/(0．5z－1+1)后的力矩测量曲线如图14中带点实线所示。可以看出，滤波后稳态误差(改变力矩0．8 ms后的误差)由2%提高至0．5%。

图14 滤波前后的力矩测量曲线Fig．14 Torque measurements before and after filtering

3 结论

本文对谐波测力技术进行了理论分析，并首次使用有限元方法对其应变片布局与力矩测量精度的关系展开研究，为谐波测力技术的优化设计提供了定性和定量依据。所设计方案能够有效削弱波发生器转动带来的干扰，实现较高的测量精度，从而为空间机器人提供了一种实用有效、紧凑化的关节力矩测量方法。

［1］Albu-Schaffer A，Bertleff W，Rebele B，et al．ROKVISS-robotics component verification on ISS current experimental results on parameter identification［C］．The 2006 IEEE International Conference on Robotics and Automation，Florida，USA，May 15－19，2006．

［2］Huang J B，Xie Z W，Jin M H，et al．Adaptive impedancecontrolled manipulator based on collision detection［J］．Chinese Journal of Aeronautics，2009，22(1):105－112．

［3］Zhao JL，Yan SZ，Wu JN．Analysis of parameter sensitivity of space manipulator with harmonic drive based on the revised response surface method［J］．Acta Astronautica，2014，98:86－96．

［4］ 游斌弟，赵阳．考虑非线性因素的谐波齿轮传动动态误差研究［J］．宇航学报，2010，31(5):1278－1282．［You Bin-di，Zhao Yang．Study on dynamic error of harmonic drive with nonlinear factors［J］．Journal of Astronautics，2010，31(5):1278－1282．］

［5］ 赵杰亮，谷勇霞，阎绍泽，等．谐波传动对柔性机械臂动力学特性的影响［J］．清华大学学报(自然科学版)，2013，53(4):482－486．［Zhao Jie-liang，Gu Yong-xia，Yan Shao-ze，et al．Effect of a harmonic drive on the dynamic properties of a flexible space manipulator［J］．J．of Tsinghua Univ．(Sci．＆Tech．)，2013，53(4):482－486．］

［6］ 谷勇霞，赵杰亮，阎绍泽，等．考虑谐波传动滞后的柔性空间机械臂运动精度［J］．机械工程学报，2013，49(23):74－79．［Gu Yong-xia，Zhao Jie-liang，Yan Shao-ze，et al．Kinematic accuracy of the flexible space manipulator with harmonic drive［J］．Journal of Mechanical Engineering，2013，49(23):74－79．］

［7］Albu-Schaffer A，Ott C，Hirzinger G．A unified passivity-based control framework for position，torque and impedance control of flexible joint robots［J］．International Journal of Robotics Research，2007，26(1):23－39．

［8］ 郭闯强，倪风雷，孙敬颋，等．具有力矩传感器的柔性关节的振动抑制［J］．机器人，2011，33(4):449－454．［Guo Chuang-qiang，Ni Feng-lei，Sun Jing-ting，et al．Vibration suppression for the flexible joint with torque sensor［J］．Robot，2011，33(4):449－454．］

［9］Kim I M，Kim H S，Song JB．Design of joint torque sensor with reduced torque ripple for a robot manipulator［J］．International Journal of Precision Engineering and Manufacturing，2012，13(10):1773－1779．

［10］Hashimoto M，Kiyosawa Y，Paul R P．A torque sensing technique for robots with harmonic drives［J］．IEEE Transactions on Robotics and Automation，1993，9(1):108－116．

［11］Taghirad H D，Belanger P R．Intelligent built-in torque sensor for harmonic drive systems［J］．IEEE Transactions on Instrumentation and Measurement，1999，48(6):1201－1207．

［12］Godler I，Ninomiya T，Horiuchi M．Ripple compensation for torque sensors built into harmonic drives［J］．IEEE Transactions on Instru．and Meas．2001，50(1):117－122．

［13］Pan X A，Wang H G，Jiang Y．A torque measuring method for robot joints with harmonic drives［C］．The 4th International Conference on Manufacturing Science and Engineering，Dalian，China，March 30－31，2013．

［14］Sensinger J W，Weir R F．Improved torque fidelity in harmonic drive sensors through the union of two existing strategies［J］．IEEE－ASME Trans．on Mech．2006，11(4):457－461．