惯导/测距/测速相结合的安全软着陆自主导航方法

吴伟仁，李 骥，黄翔宇，张洪华，王大轶，张 哲

(1．国防科工局探月与航天工程中心，北京100037;2．北京控制工程研究所，北京100190;3．空间智能控制技术国家级重点实验室，北京100190)

0 引言

地外天体软着陆探测是深空探测的一种重要方式。到目前为止，美国、苏联、欧空局以及日本等国家和组织已经先后对月球、火星、小行星和彗星等地外天体实施了软着陆探测。以嫦娥三号为代表，我国也实现了月球软着陆探测［1］，未来还将开展对火星、小行星等深空天体的着陆探测。

由于地外天体距离地球都很遥远，地面测控在实时性和精确性上很难满足要求，因此着陆过程的导航一般都采用自主导航。在已经实现的着陆探测任务中，美国的Surveyor［2］和Apollo［3］采用了基于惯性测量单元(以下简称IMU)、雷达高度计和多普勒速度敏感器的导航方式;苏联的lunar系列也采用的是陀螺、加速度计(以下简称加计)、多普勒测速仪和测高仪的导航方式［4］;我国的嫦娥三号月球探测器在软着陆过程中则采用了IMU、激光测距仪和微波测距测速敏感器组合的导航方式［5］。目前，各国正在研制的新一代着陆探测器则进一步突出了着陆导航精度。例如，日本的Selene-B计划采用IMU、光学导航相机、激光高度计/测速仪的复合导航方法［6］;欧空局研制中的月球着陆器采用了IMU、距离传感器和导航相机相组合的导航方法［7］;美国原计划开展的星座计划项目，甚至设计了一套融合光学图像、测距测速以及地面无线电测量的导航方法，形成一种天地一体的组合导航方案［8］。

为确保地外天体软着陆任务中，着陆器能够以尽可能小的速度垂直降落到天体表面理想区域，导航系统需要提供准确的相对天体表面的高度和速度(包括垂向和水平共三个方向)信息，至于水平位置信息则处于相对次要的地位。因此尽管具体方案千差万别，采用的敏感器在工作体制、性能指标上也不尽相同，但惯导结合测距以及测速修正的导航方式始终是地外天体软着陆自主导航的核心。其中惯导是提供位置、速度和姿态测量的基本手段，测距用于修正惯导的高度误差，测速则用于修正惯导的三维速度误差。在这三者的组合下就提供了安全软着陆的基本导航手段。本文以此为基础，对惯导、测距和测速及在工程实用中会遇到的地形问题进行了详细的数学建模和理论分析，并给出了相关计算方法和修正策略。

1 惯性导航

1．1软着陆运动学模型

取天体中心惯性系为参考坐标系(用i表示)，软着陆平动运动学方程可以描述为

式中:ri是着陆器位置矢量在惯性系下的表示(3×1列向量)，vi是着陆器速度矢量在惯性系下的表示(3×1列向量)，μ是天体中心引力常数，Fi是除引力外作用在着陆器上的合外力矢量在惯性系下的表示(3×1列向量)，m是着陆器的质量，是引力摄动加速度矢量在惯性系下表示(3×1列向量)。

着陆器本体相对惯性系的姿态用四元数q=［q1，q2，q3，q4］T表示，运动学方程可以描述为

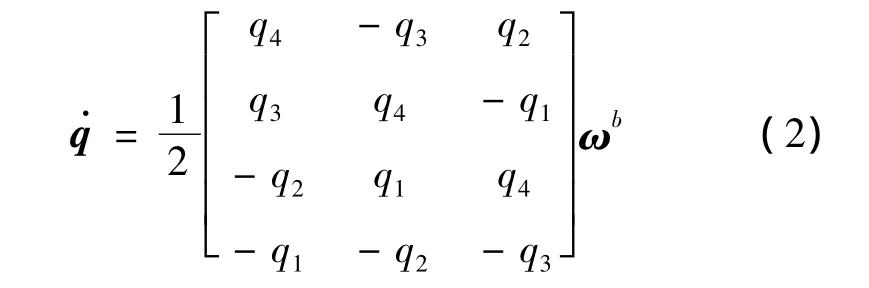
式中:ωb是角速度矢量在着陆器本体系(用b表示)下的表示(3×1列向量)，它可以根据陀螺测量得到。式(1)和式(2)构成了着陆过程的基本运动学方程，它们也是惯性导航解算的基础。

1．2惯导基本方程

1)惯导位置、速度外推

惯性导航的基本测量源为IMU，它包含三个正交的陀螺和三个正交的加计，整个组件以捷联方式安装在着陆器本体上。其中陀螺可以获得本体相对惯性空间的角速度，加计可以获得作用在本体上的非引力加速度。假设本体系下非引力加速度的测量值为，由于在轨飞行中加计的零偏和刻度因子都可以进行标定，扣除这些因素后有

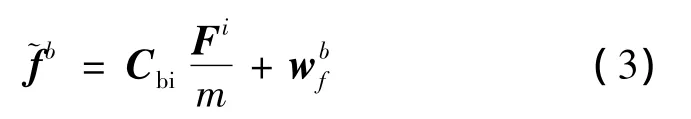
式中:Cbi是本体相对惯性系的姿态矩阵，是加计的测量噪声向量在着陆器本体系下的表示。

将式(3)代入式(1)，则有

2)惯导姿态外推

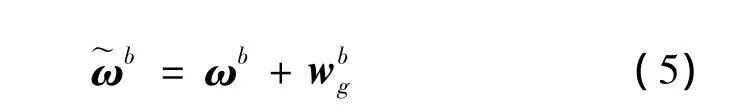
将式(5)代入式(2)中有

将式(4)和式(6)结合起来就可以进行运动学外推，即惯导外推。惯导外推有很多具体的算法，例如嫦娥三号着陆器所使用的四子样算法等［5］。但无论哪种算法，都可以用基本方程(4)和(6)来表示。

1．3惯导在着陆导航中的不足

基于递推算法的惯性导航中，由于各种误差的累积作用，惯导计算误差逐渐增大。图1和图2是某月球软着陆任务中仿真得到的惯导高度误差和垂直速度误差随时间的变化曲线，其中点划线是蒙特卡洛仿真统计的均值，虚线是蒙特卡洛仿真中获得的最大值，实线为统计得到的3σ界。很显然，惯导的高度和速度误差均呈发散状态。这说明单纯依靠惯导无论是在高度还是在速度上都很难满足安全着陆的需要。

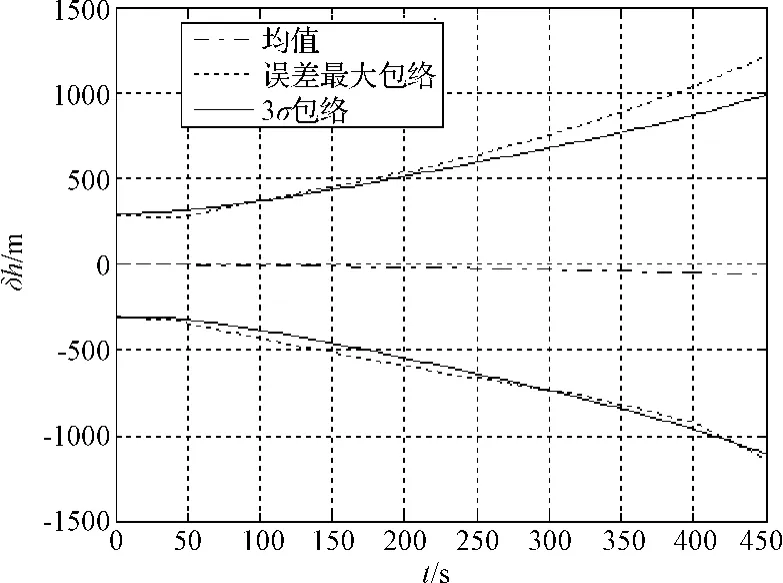
图1 惯导高度误差曲线Fig．1 INSerror in altitude

2 测距对惯导高度的修正

2．1地形模型

测距仪得到的是着陆器沿测距仪波束方向相对天体表面的直线距离，而惯性导航提供的是相对天体中心的位置，这意味着惯性导航不能直接给出相对天体表面的高度。两者之间存在地形影响。

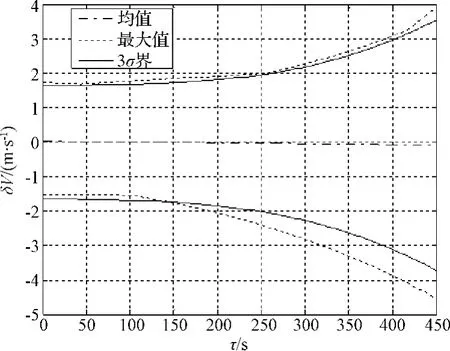
图2 惯导垂直速度误差曲线Fig．2 INSerror in vertical velocity

以月球虹湾地区为例，动力下降的典型航迹如图3所示。图中，纵向白线为航迹，箭头表示飞行方向。该航迹下的地形起伏如图4所示。

图3 月球着陆过程的典型航迹图Fig．3 Typical landing trajectory of lunar landing

月面地形可以建模为趋势项和叠加在该趋势项上的高度起伏。对于虹湾地区来说，其趋势项可以建模成斜坡

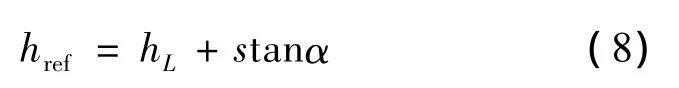
式中:hL是基准高度，s是着陆航程，α是坡度。

图4 典型航迹下的月面起伏Fig．4 Terrain under the typical landing trajectory

高度起伏可以用一阶马尔科夫过程描述，即

β是相关距离。

由于航程实际是水平速度的积分，即

式中:vhor表示水平速度，因此式(9)可以变为

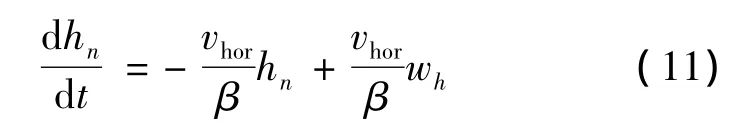
显然，随着高度的降低，着陆器水平速度越来越小，则地形的起伏变化也越来越小。

2．2测距模型

测距仪测量的是沿波束方向到实际月面的斜距。将它解算为高度时，需要用到着陆器的姿态信息。假设测距波束方向在本体系的表示为，测距仪的斜距测量值为，那么测距仪解算的高度为

测距仪解算的高度与实际星下点高度是有偏差的，包括测距仪自身的测量误差以及测距仪指向与铅垂线之间夹角带来的地形起伏误差(如图5所示)。为了降低后者的影响，通常在着陆器本体向下的方向会安装一个测距波束天线或装置。这样当着陆器最终以垂直方式着陆时，该波束方向与铅垂线方向一致，地形起伏的影响得以消除。

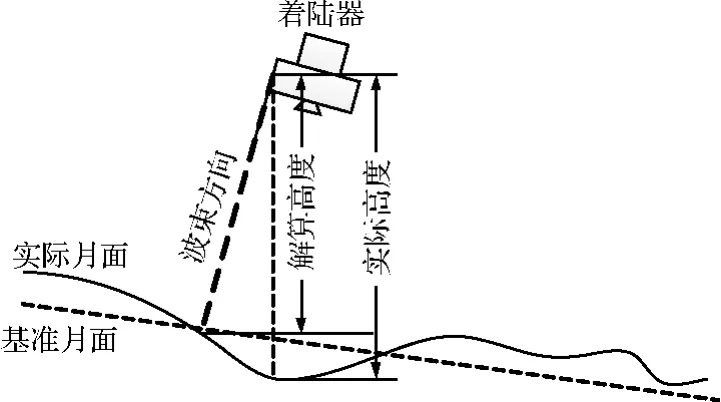
图5 测距仪测量原理Fig．5 Measurement geometry of altimeters

2．3测距修正

测距仪解算的高度与着陆器位置之间有如下关系

式中:Rm是天体参考半径，δhalt是测距仪高度解算的随机误差。

对于测距修正来说，只有垂向通道的惯导误差(高度和垂向速度)是可观测的［10］，因此不能按照式(4)、(6)和(13)建立全状态的滤波方程。着陆器的垂向运动学方程可以近似为

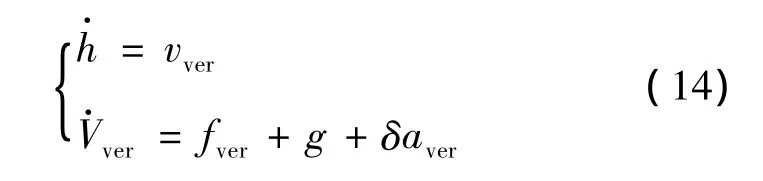
式中:vver表示垂向速度，fver是垂向非引力加速度，g是重力加速度，δaver是纵向加速度误差。h是着陆器相对天体参考半径Rm的高度(称为绝对高度)，它与着陆器位置r的关系为

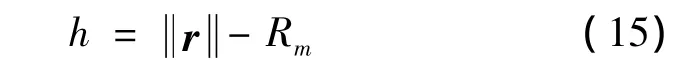
测距仪测量出波束方向的斜距，并按式(12)可以解算出相对实际天体表面的高度(称为相对高度)，那么由式(13)可以得到测量方程为

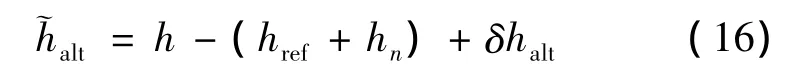
由式(11)可知hn随速度越来越小，因此将hn与测距仪误差δhalt一起考虑为随机量。假设href已知，那么可以建立滤波的状态方程和测量方程

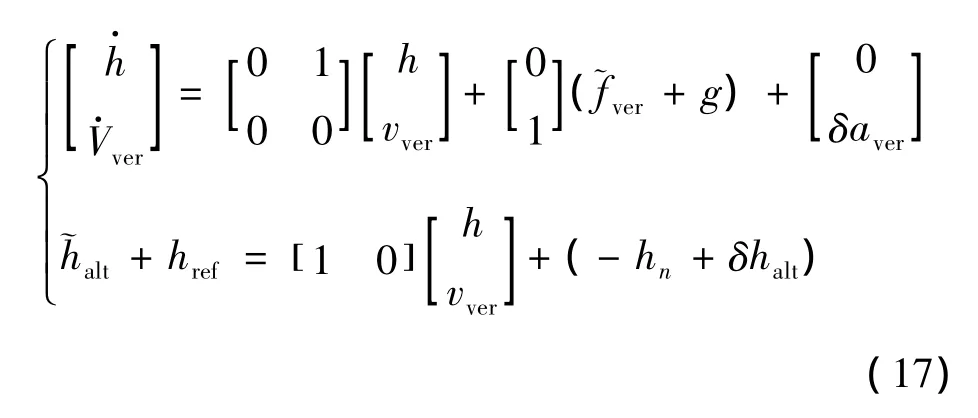
需要说明的是，导航系统应该提供着陆器相对天体实际表面的高度，即相对高度，而由式(17)估计的高度是绝对高度，那么为计算相对高度还应当补偿掉已知地形，即

理论上，测距修正除了能够估计出着陆器的高度外还应估计出垂直速度，但是实际估计出的垂直速度并不是特别准确。在地外天体着陆过程中href通常并不知道。将式(17)进行适当变换，有

式(19)可用来对着陆器相对天体地形趋势项的高度和垂直速度进行估计，方程的右边出现了天体地形趋势项的变化率，即。由于地外天体着陆任务中地形趋势往往事先不知，因此在式(19)中只能假定这个变化率为0。但实际上，只要趋势面存在高度变化，那么href对时间的导数在着陆器转为垂直飞行之前就不为0，由此滤波估计出的垂向速度就会出现偏差。但相对高度是直接观测量，受地形不确定的影响较小，即使href没有先验知识，对高度估计效果的影响也可忽略。

3 测速对惯导速度的修正

对于着陆安全性来说，水平速度为0是避免着陆器接触天体表面时发生翻倒的一个重要前提。为了提高水平速度精度，导航还必须引入直接的速度测量修正。为了构建完整的三维空间速度矢量，需要有三个不共面的测速波束。

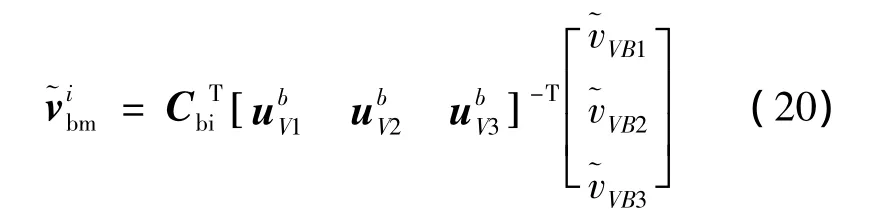
惯导提供的是着陆器相对惯性系的速度，而惯性系的速度与相对天体表面的速度之间存在如下关系

那么根据式(4)和(21)，可以构造滤波方程

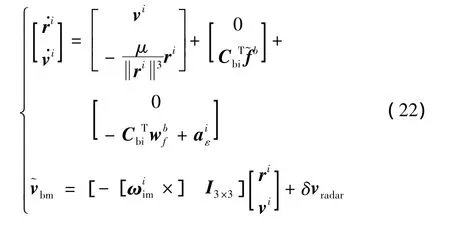
式中:δvradar是测速敏感器测量误差，I3×3表示3×3单位矩阵。对式(22)可以使用扩展卡尔曼滤波进行估计，其中ri、vi的时间更新部分就是惯导位置、速度的外推。

从文献［10］已知上述系统是完全可观的，但对天体自转角速度，即的模，比较小的天体(例如月球)，式(22)中ri的可观性并不太好。对于这种情况，可以将ri视为已知量(由惯导提供)，这样被估状态就只剩下vi，与之相对应，滤波器变为

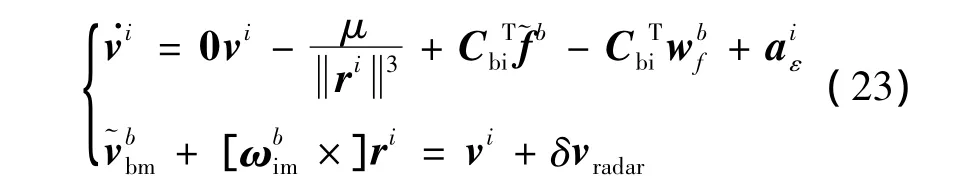
这是一个线性定常系统，可以使用卡尔曼滤波进行状态估计。工程实践时，也可以将它转换为固定系数滤波器，但滤波系数应随高度或速度变化［5］，通常的趋势是滤波系数随高度降低或速度下降而增大。

4 组合使用的策略

从安全着陆的角度看，着陆过程的导航精度应随着高度的降低逐渐提高。惯性导航本身的误差是逐渐增大的，而测距和测速仪的误差会随着高度的降低逐渐减小，两者的精度水平可能会在某一高度下形成交叉。例如，某月球着陆器惯导和测距仪解算高度的精度水平以及惯导和测速仪精度水平的对比情况分别如图6和图7所示，图中实线表示INS的误差，点划线表示测距或测速的误差，线段长度按照敏感器作用距离绘制。这表明，测距和测速修正并不一定需要在下降的全程都引入，只要保证在着陆后期(测距测速精度高于惯导以后)启用，这样也有利于降低敏感器研制的难度。

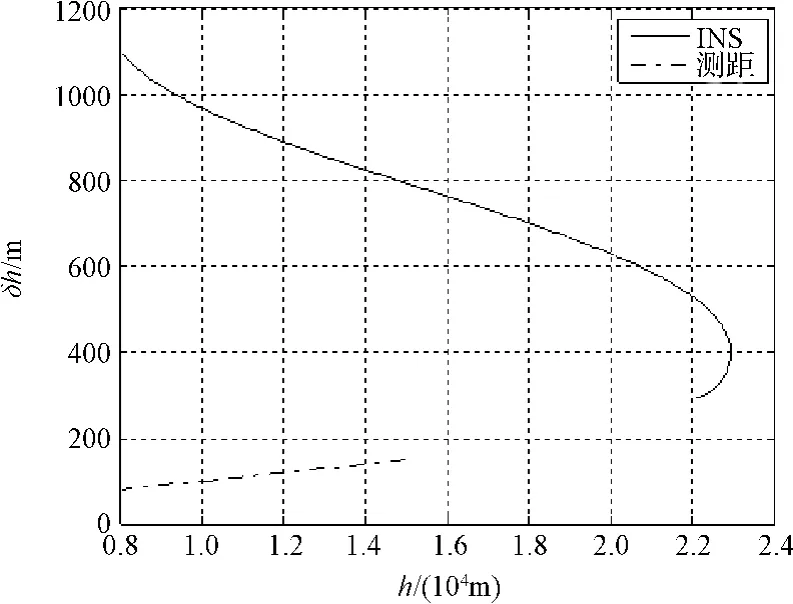
图6 测距仪与惯导高度解算精度比较Fig．6 INSand altimeter errors

图7 测速仪与惯导速度解算精度比较Fig．7 INSand Doppler velocimetry errors

5 仿真校验

以月球软着陆过程为例，对惯导/测距/测速相结合的自主导航方法进行仿真校验。仿真过程中假定着陆器从15×100 km的椭圆环月轨道近月点开始下降。测距修正从8 km高度开始引入;测速修正从4 km高度开始引入。

着陆过程的高度变化曲线如图8所示。其中实线为实际飞行高度曲线，虚线为导航给出的高度变化曲线，点划线是地形。由于初始测定轨误差的存在，下降的初始阶段导航给出的高度相比实际高度存在偏差，到8 km测距修正引入后，导航高度偏差迅速缩小。

图8 月球软着陆主减速过程的飞行轨迹Fig．8 Altitude vs time in lunar landing

着陆过程的速度误差变化曲线如图9所示，其中δVx、δVy和δVz分别表示惯性系下三方向的速度误差。很明显在测速修正引入以前，惯导的速度误差处于发散状态。当测速修正引入后，速度误差迅速趋于0，并在0附近波动。

图9 月球软着陆过程导航速度误差变化Fig．9 Velocity vs time in lunar landing

6 结论

地外天体软着陆对导航系统而言，保证安全就是保证高度和速度三方向分量的精度。从这一根本要求出发，本文分析了惯导、测距仪和测速仪在着陆任务中的作用，对它们各自的原理、模型、算法、性能、优缺点和组合使用方法等进行了详细的介绍和推导。并从工程实际出发，针对计算量、地形影响、滤波稳定性等问题，利用可观性分析的结论，对测速、测距修正的算法进行了简化。相比各种理论算法，本文介绍的安全软着陆导航方法实用性更强。数学仿真表明基于惯导和测距/测速组合修正的安全软着陆自主导航方法能够保证导航系统在高度和速度上的精度，满足安全软着陆的基本需要。

［1］ 张洪华，关轶峰，黄翔宇，等．嫦娥三号着陆器动力下降的制导导航与控制［J］．中国科学:技术科学，2014，44(5):377－384．［Zhang Hong-hua，Guan Yi-feng，Huang Xiang-yu，et al．Guidance navigation and control for Chang’E-3 powered descent［J］．Scientia Sinica:Technologica，2014，44(5):377－384．］

［2］Beilock M．Surveyor lander mission and capability［R］．JPL Technical Report No．32－618，1964．

［3］Bennett F V．Apollo experience report-mission planning for lunar module descent and ascent［R］．NASA TN D－6846，1972．

［4］Beresnev N P，Legonstayev V P．Control system for automatic station lunar-9［R］．A67－39167，1967．

［5］ 张洪华，李骥，关轶峰，等．嫦娥三号着陆器动力下降的自主导航［J］．控制理论与应用，2014，31(12):1686－1694．［Zhang Hong-hua，Li Ji，Guan Yi-feng，et al．Autonomous navigation for powered descent phase of Chang’E-3 lunar lander［J］．Control Theory＆Applications，2014，31(12):1686－1694．］

［6］Sawai S．SELENE-B navigation and guidance system for pinpoint landing［C］．The 3rd Space Science Symposium in ISAS，Sagamihara/Kanagawa，Japan，2003．

［7］Kerr M L，Hagenfeldt M，Ospina JA，et al．ESA Lunar Lander:Approach phase concept and G＆C performance［C］．AIAA Guidance Navigation and Control(GNC)Conference，Boston，MA USA，August 19－22，2013．

［8］Ely T A，Heyne M，Riedel J E．Altair navigation performance during translunar cruise，lunar orbit，descent，and landing［J］．Journal of Spacecraft and Rockets，2012，49(2):295－317．

［9］ 李骥，张洪华，赵宇，等．嫦娥三号着陆器的陀螺在轨标定［J］．中国科学:技术科学，2014，44(6):582－588．［Li Ji，Zhang Hong-hua，Zhao Yu，et al．In-flight calibration of the gyros of the Chang’E-3 lunar lander［J］．Scientia Sinica:Technologica，2014，44(6):582－588．］

［10］ 王大轶，黄翔宇，关轶峰，等．基于IMU配以测量修正的月球软着陆自主导航研究［J］．宇航学报，2007，28(6):1544－1549．［Wang Da-yi，Huang Xiang-yu，Guan Yi-feng，et al．Research on the autonomous navigation based on measurementupdated IMU for lunar soft landing［J］．Journal of Astronautics，2007，28(6):1544－1549．］

［11］ 秦永元，张洪钺，汪叔华．卡尔曼滤波与组合导航原理［M］．西安:西北工业大学出版社，1998:33－55．