对提升学生数学思维品质的思考
马奇飞
[摘 要]培养学生的思维能力,提升学生的思维品质是数学教学的一个重要任务。这就要求教师在教学中通过对比、观察、求异等方法,引导学生学会学习、学会思维,进而提升学生的数学思维品质。
[关键词]小学数学 思维品质 提升 深刻性 灵活性 创造性 批判性
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2015)36-025
数学是思维的体操,因此,如何培养和提升学生的思维品质成为数学教学中的一个重要任务。下面,笔者结合自己的教学实践,谈一些做法和体会。
一、借对比,挖内涵,培养思维的深刻性
思维的深刻性就是指思维的深度,是发现和辨别事物本质的能力。在认识事物时,若缺少对其本质深刻的揭示,思维的灵活性、批判性就无从谈起。因此,培养思维的深刻性,往往是培养其他思维品质的立足点和突破口。
例如,教学“小数点移动引起小数变化”这一知识时,不少教师觉得这一知识点简单易懂,因为学生很容易掌握一个小数乘(除以)10、100、1000的算理,即只要将小数点向右(左)移动一位、两位、三位就可以了。其实,对学生而言,小数点的移动只是一种视觉表象,即从原位置移到另一位置,这说明他们没有真正理解小数点变化的内涵。教师可以这样教学:“为什么一个小数乘或除以10、100、1000时小数点可以直接移动,而乘或除以其他非整十数时不能直接移动小数点呢?因为乘或除以10、100、1000的变化符合十进制规律。”在具体讲解时,教师可以对着数位顺序表将原小数写好,再将变化后的小数也对着数位顺序表写好,然后将两数对比,引导学生寻找小数前后的变化,使学生发现并理解小数点移动引起小数变化的真正内涵。
二、多观察,善变通,培养思维的灵活性
思维的灵活性是指善于从不同角度和不同层次进行分析思考。学生解题的思路广、方法多、解法好,就是思维灵活的表现。因此,数学教学中,教师要注重启发学生从不同角度思考问题,鼓励联想,提倡一题多解。同时,教师应设计开放性练习,促进学生思维灵活性的发展。
例如,教学“乘法分配律”后,部分学生虽然能熟练地背出公式,但大多记住的只是运算律的外在形式,在综合练习、变式练习时往往无从下手。如简便计算10.8×37+6.3×108时,因为算式中没有出现相同的数,所以学生找不到特征,无从下手。其实,只要运用积的变化规律变化一下,如变成10.8×37+63×10.8或108×3.7+6.3×108,问题就会迎刃而解。在日常教学中,教师不能让学生生搬硬套公式,面对灵活多变的问题,要引导学生多观察,广开思路,寻找问题的症结,从而成功解决问题。
三、反常规,促辨析,培养思维的批判性
思维的批判性是指检查思维的过程,善于独立思考,不受常规干扰;善于发现问题、提出质疑,不断分析解决问题所依据的条件,反复检查已拟定的假设、计划和方案;善于客观地考虑正反两方面的论据;善于明辨是非曲直,不人云亦云,不盲从附和。
例如,教学“找规律”(覆盖规律)后,我设计了这样一道综合练习题:“用长方形去框下面的一列数,每次同时框出两个数,一共可以框出多少种不同的和?”
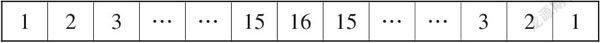
绝大多数学生列式为31-2+1=30,很明显,学生只会生搬硬套公式,忽略了两数之和相同的重复情况。
四、倡求异,破常规,培养思维的创造性
新课程提倡标新立异,鼓励学生探究求新,对问题创造性地寻找独特、简洁的解法,这些都能促进学生创造性思维的发展。
例如,一道来源于实践活动“铺地砖”的练习题:“教师节快到了,同学们分小组做贺卡打算送给老师,现在每小组都有一张长45厘米、宽35厘米的长方形卡纸,最多能做多少张长15厘米、宽10厘米的长方形贺卡?(不可以拼接)”学生尝试解题后反馈结果:解法(1)45÷15=3,35÷10=3……5(厘米),3×3=9(张);解法(2)35÷15=2……5(厘米),45÷10=4……5(厘米),2×4=8(张)。学生认可最多能做9张长方形贺卡是最佳答案,教师追问:“为什么解法(1)与解法(2)的思维一样,而结果却不同呢?有没有想过这两种思路可以结合使用?”问题提出后,学生再一次深入思考。这时,突然有学生说:“可以剪10张长方形贺卡。因此将横着放、竖着放相结合,可将长方形卡纸分为两部分,一部分长45厘米、宽20厘米,横着放可做6张长方形贺卡;另一部分长45厘米、宽15厘米,竖着放可做4张长方形贺卡,所以一共能做10张长方形贺卡。”顿时,教室里响起了热烈的掌声……
总之,课堂教学中,教师应通过各种方式引导学生学会学习、学会思维,不断提升学生的数学思维品质,使学生在数学学习上得到不同的发展。
(责编 杜 华)

