由果索因 重视推理 激发思维

陈乃春

在一次校内同课异构的教研活动中，我校两位教师均执教“相邻体积单位间的进率”一课，因为对教学环节的不同处理，所取得的教学效果也不尽相同。

教材例题：

■

A教师：

1.教学例题

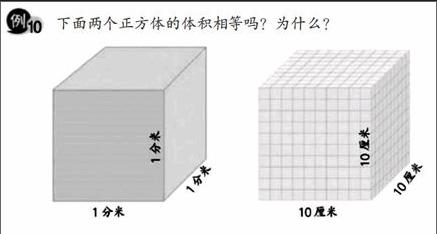
师（出示例题中的两个正方体）：这两个正方体的体积相等吗？为什么？

（学生独立计算，师巡视）

2.汇报交流

生：棱长是1分米的正方体，它的体积是1立方分米;棱长是10厘米的正方体，它的体积是1000立方厘米。

师生共同得出结论：棱长1分米的正方体和棱长10厘米的正方体体积相等，即1立方分米=1000立方厘米。

……

B教师：

1.复习引新

师：同学们，我们已经学过长度单位、面积单位之间的进率，那你们知道1分米等于多少厘米吗？1平方分米等于多少平方厘米呢？

师：你能猜一猜1立方分米等于多少立方厘米吗？（指名学生回答）

师：为什么1立方分米等于1000立方厘米？你能说说理由吗？

2.学生交流

生1：1分米等于10厘米，由于棱长为1分米的正方体体积与棱长为10厘米的正方体体积一样大，而棱长为1分米的正方体体积是1×1×1=1（立方分米），棱长为10厘米的正方体体积是10×10×10=1000（立方厘米），所以1立方分米等于1000立方厘米。

师：你说得非常清楚。还有其他方法也能说明1立方分米等于1000立方厘米吗？

生2：如果在一个棱长为1分米的正方体容器里摆放棱长为1厘米的小正方体，先沿着长摆10个小正方体，再沿着宽摆这样的10行，这样一层就能摆100个小正方体，然后沿着高摆这样的10层，因为100×10=1000，所以1立方分米等于1000立方厘米。

生3（补充）：也可以把一个棱长为1分米的正方体木块切割成1000个棱长为1厘米的小方块，同样说明1立方分米等于1000立方厘米。

师：怎么切呢？

生3：沿着长可以切10列，沿着宽可以切10排，沿着高可以切10层，这样就切出了1000个小正方体。

师：你们通过拼、切的方法，的确都能说明1立方分米等于1000立方厘米。

生4：因为我们学过升和毫升之间的进率是1000，而1升等于1立方分米、1毫升等于1立方厘米，所以1立方分米等于1000立方厘米。

师：你能联系以前学过的知识推导出现在学习的知识，真不错！

……

思考：

上述教学中，A教师从教材例题入手，让学生通过观察和计算得到1立方分米=1000立方厘米的结论;B教师则先引导学生回顾相关的长度单位、面积单位的进率，引发学生对体积单位的进率进行猜想，再组织学生对猜想的结果进行验证。

比较这两个教学案例，A教师的教学采用由因导果的方法，引导学生对条件进行分析后得出结论，这样的教学注重知识的习得，符合学生的认知规律。但这样教学，学生很明显是被教师牵着走的，处于被动接受知识的状态，尽管最终也达成了认知目标，学生的思维含量却不高。

B教师的教学重视学生推理能力的培养。课始，教师就调动学生的已有认知和经验，引导学生对新的知识进行合情（类比）推理。在这样的学习过程中，学生的思维被激发，能够主动结合已有的认知对猜想的结论从多个角度进行验证。“语言是思维的外壳”，在验证的过程中，学生很好地运用“因为……所以……”“先……再……”等句式进行表达，并且做到思路清晰、言之有理、推之有据，形成了一定的逻辑推理模式。整个过程由果索因，学生的思维完全被激发，在知识习得中体会并主动运用了推理的思想方法，既使思维能力得到提高，又提升了数学素养。

对比这两个教学案例，引发了我们很多的思考。A教师的教学由因导果，B教师的教学由果索因，对同一个教学环节的不同处理，获得了不同的教学效果。在课程改革深入实施的今天，我们已经清醒地认识到教师的教学方法、学生的学习方式等并没有所谓的“好”与“不好”之分，教学改革不是简单的扬弃。A教师的教学由因导果也好，B教师的教学由果索因也罢，都符合学生的认知发展规律，但我们要做的是应该追求学生思维效益的最大化。面对学习材料，教师如何在有限的时间和空间内运用更合理的方式进行教学，引导学生积极主动地参与问题的探究？数学课堂如何充分发挥其在培养人的思维能力的作用？这也许是我们每一位数学教师都要思考的问题。

（责编 杜 华）endprint