5阶Bézier型曲线及其应用

5阶Bézier型曲线及其应用

车 毅，熊 建
(安徽审计职业学院基础部，合肥 230601)

为了精确表示椭圆弧、圆弧等二次曲线及摆线、螺旋线等超越曲线，在非多项式空间{1，t，sint，cost，sin 2t}中，构造了一种5阶Bézier型基函数，其具有Bernstein基的类似性质，诸如非负性、规范性、对称性、端点性质等。由此基函数构造的5阶Bézier型曲线，具有Bézier曲线基本性质，诸如凸包性、对称性、几何不变性及端点插值和边界相切性质。给出了5阶Bézier型曲线C1连续及G1连续光滑拼接条件及在旋转曲面造型中的应用实例。试验表明，此造型方法是有效的，丰富了造型技术理论。

5阶Bézier型基;5阶Bézier型曲线;拼接;二次曲线;超越曲线

在机械加工、航天航空等领域，经常出现二次曲线弧及超越曲线表示的形状，且许多零部件都是由一个或多个旋转曲面构造而成。因此，对于二次曲线及超越曲线的精确表示及旋转曲面造型的研究显得尤为重要。Bézier曲线因其优良性质在自由曲线曲面造型中被广泛应用，但它不能精确描述椭圆等二次曲线及超越曲线。NURBS方法虽然可以精确表示二次曲线，但其求导求积计算及权因子选取都较为复杂［1，2］。为了解决这些方法的局限性，非多项式空间中的曲线曲面造型方法应运而生。张纪文［3］等在空间{1，t，sint，cost}中构造了C-曲线，Chen［4］等对C-Bézier曲线进行推广，郭清伟［5］等对C-Bézier曲线进行多形状参数的扩展;苏本跃［6］等在T3={1，sint，cost}，T4={1，sint，cost，cos 2t}，T5={1，sint，cost，sin 2t，cos 2t}中构造了一种称为T-Bézier的Bézier型曲线，一些学者对其展开研究，构造了一些带形状参数的CT-Bézier曲线［7-12］;Mainar与Peňa［13］构造了T6={1，t，sint，cost，sin 2t，cos 2t}，T5={1，t，t2，sint，cost}和T6={1，sint，cost，tsint，tcost}中的标准化B基;严兰兰等构造了二、三阶三角Bézier曲线及五、六阶三角样条曲线［14-15］。

苏本跃［6］等在T5={1，sint，cost，sin 2t，cos 2t}中构造的五阶T-Bézier曲线可以精确表示椭圆弧、圆弧等二次曲线，但不能精确表示摆线、螺旋线等超越曲线。本文在非多项式空间{1，t，sint，cost，sin 2t}中构造了5阶Bézier型基函数，它具有Bernstein基的类似性质。由此构造的5阶Bézier型曲线，具有Bézier曲线类似的优良性质，诸如端点插值与边界相切性、对称性、凸包性及几何不变性等。除此之外，它可以精确表示椭圆弧、圆弧等二次曲线及摆线、螺旋线等超越曲线。文中给出了曲线段的拼接条件，运用拼接曲线可以构造旋转曲面。最后，给出了应用的具体实例，验证了本文构造的曲线是有效的。本文造型方法丰富了曲线曲面造型理论，为造型技术提供了另外的选择。

1 5阶Bézier型曲线结构及其性质

1.1 基函数定义及性质

定义1设0≤t≤，称

为5阶Bézier型基函数，其中

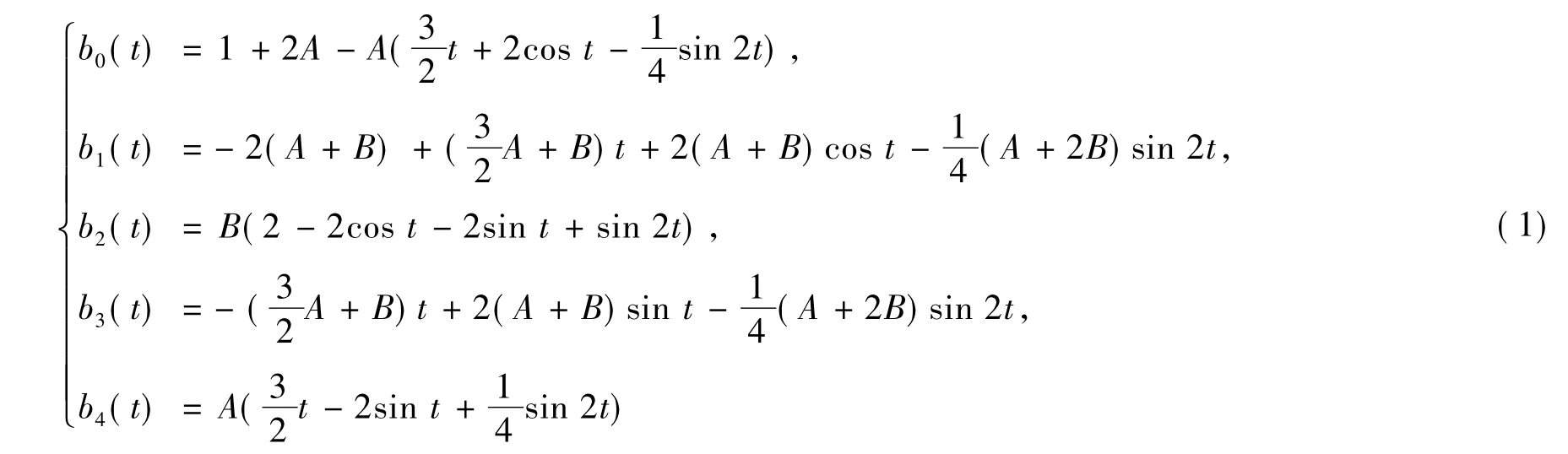
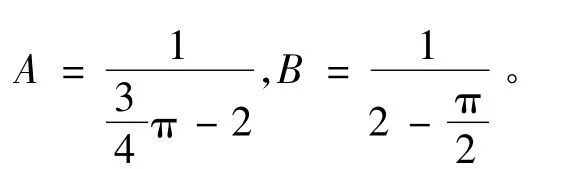
5阶Bézier型基函数的性质如下:

证明由定义1中式(1)直接计算易证性质2，3，4。下证性质1。

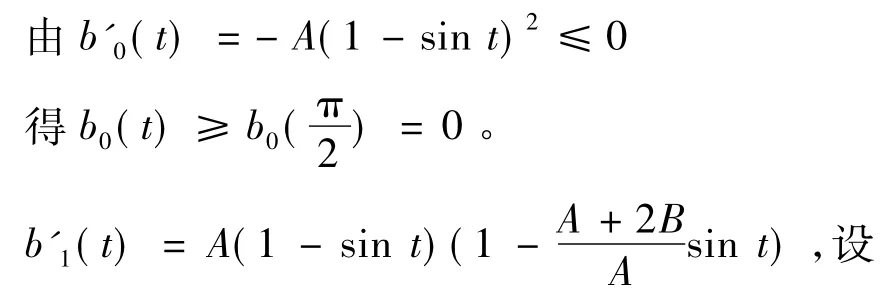
由性质3对称性可得b3(t)≥0，b4(t)≥0。

图1给出了5阶Bézier型基函数图。

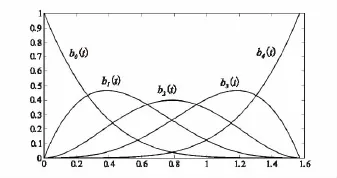
图1 5阶Bézier型基函数

1.2 5阶Bézier型曲线定义及性质

定义2对于给定的5个控制顶点Pi(i=0，1，2，3，4)，0≤t≤，称为 5阶Bézier型曲线。

5阶Bézier型曲线的性质:

性质5端点插值与边界相切性

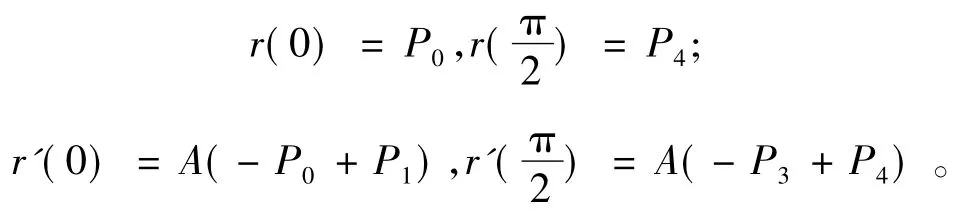
性质6对称性

对于给定控制多边形P0P1P2P3P4，自P0开始构造的5阶Bézier型曲线与自P4开始反向构造的5阶Bézier型曲线形状完全相同，但参数化的方向相反。

性质7凸包性

定义2的曲线位于控制顶点{Pi}(i=0，1，2，3，4)张成的凸包内。

性质8几何不变性

5阶Bézier型曲线的形状与坐标系的选取无关。

由性质1，2，3，4及定义2易证性质5，6，7，8。

2 5阶Bézier型曲线应用

2.1 5阶Bézier型曲线精确表示二次曲线及超越曲线

运用5阶Bézier型曲线可以精确表示椭圆弧、圆弧等二次曲线以及摆线、螺旋线等超越曲线。

定理1设5个控制顶点P0(x0，y0)，P1(x1，y1)，P2(x2，y2)，P3(x3，y3)，P4(x4，y4)，对于 5阶Bézier型曲线

图2给出了5阶Bézier型曲线精确表示的一段椭圆弧x2/16+y2/9=1及相应的控制多边形。图3给出了5阶Bézier型曲线精确表示的一段摆线(x(t)，y(t))=(4(t－sint)，4(1－cost))及相应的控制多边形。图4给出了5阶Bézier型曲线精确表示的一段螺旋线 (x(t)，y(t)，z(t))= (6cost，6sint，4t)及相应的控制多边形。

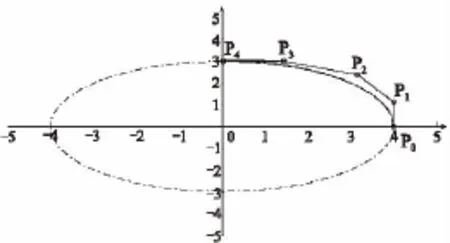
图2 5阶Bézier型曲线表示的椭圆弧及其控制多边形

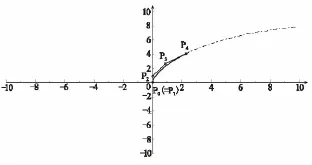
图3 5阶Bézier型曲线表示的摆线弧及其控制多边形

2.2 5阶Bézier型拼接曲线构造旋转曲面

一条平面曲线绕其平面上的一条固定直线旋转一周产生的曲面称为旋转曲面，其中平面曲线和定直线依次叫做旋转曲面的母线和轴。在机械加工、航天航空等领域，许多零部件都是由一个或多个旋转曲面构造而成。显然，旋转曲面形状主要取决于母线形状。利用5阶Bézier型曲线段进行拼接，构造出Bézier型曲线作为母线，再构造旋转曲面。

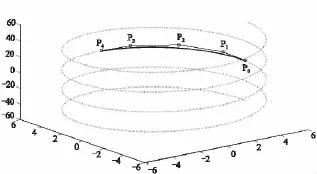
图4 5阶Bézier型曲线表示的螺旋线一段及其控制多边形

经计算，结论得证。

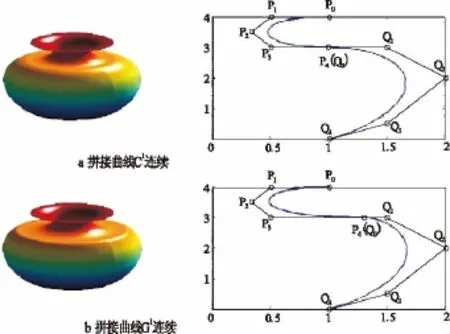
图5 花瓶造型图

图5给出了两5阶Bézier型曲线段C1拼接及G1拼接得到的Bézier型曲线作为母线绕z轴旋转得到的花瓶造型实例。其中图5a中拼接曲线C1连续其控制顶点分别为P0(1，4)P1(1/2，4)P2(1/3，7/2)P3(1/2，3)，P4=Q0(1，3)，Q1(3/2，3)，Q2(2，2)，Q3(3/2，1/2)，Q4(1，0)，图5b中拼接曲线G1连续其控制顶点除P4=Q0(1.3，3)外，其它不变。

3 总结

本文给出了一种新的曲线生成方法。由此生成的曲线具有Bézier曲线的性质，可以精确表示椭圆弧、圆弧等二次曲线和摆线、螺旋线等超越曲线，且计算简便。运用曲线段进行拼接，可以生成C1或G1连续的整条曲线，以此作为母线，可以生成旋转曲面。实例验证了本文方法是有效的。

［1］施法中.计算机辅助几何设计与非均匀有理B样条［M］.北京:高等教育出版社，2001.

［2］王国瑾.计算机辅助几何设计［M］.北京:高等教育出版社，2001.

［3］Zhang J W.C-Bézier curves and surfaces［J］.Graphical Models and Image Processing，1999，61(1):2-15.

［4］Chen Q Y，Wang G Z.A class of Bézier-like curves［J］.Computer Aided Geometric Design，2003，20 (1):29-39.

［5］郭清伟，熊 建，朱功勤.C-Bézier曲线曲面的扩展［J］.计算机工程与应用，2009，45(12):170-173.

［6］苏本跃，黄有度.一类Bézier型的三角多项式曲线［J］.高等学校计算数学学报，2005，27(3):14-20.

［7］王刘强，刘旭敏.T-Bézier曲线及G1拼接条件［J］.计算机工程与应用，2007，43(1):47-49，60.

［8］吴晓勤，韩旭里，罗善明.带形状参数的二次三角Bézier曲线［J］.工程图学学报，2008，29(1):82-87.

［9］王刘强，刘旭敏.带形状参数的二次TC-Bézier曲线［J］.计算机工程与设计，2007，28(5):1096-1097，1125.

［10］马素静，刘旭敏.二次均匀TC-B样条曲线的扩展［J］.计算机工程与设计，2008，29(22):5863-5865.

［11］马素静，刘旭敏.带形状参数的三次TC-Bézier曲线［J］.计算机工程与设计，2009，30(5):1151-1153.

［12］徐迎博，喻德生.带形状参数的二次三角多项式Bézier曲线形状分析［J］.浙江大学学报:理学版，2013，40(1):35-41.

［13］Main E，Peňa J M，Sanchez-Reyes J.Shape preserving alternativesto the rational Bézier model［J］.Computer Aided Geometric Design，2001，18(1):37-60.

［14］严兰兰，韩旭里，邬国根，等.二/三阶三角Bézier曲线［J］.图学学报，2013，34(5):71-75.

［15］严兰兰，韩旭里，黄 涛.五阶与六阶三角样条曲线［J］.图学学报，2014，35(2):200-207.

Bézier-type curve of 5 order and its applications

CHE Yi，XIONG Jian
(School of Basics，Anhui Audit Vocational College，Hefei Anhui230601，China)

To represent some quadric curves and transcendental curves，such as elliptic arc，circular arc，cycloid and helix，a new kind of Bézier-type basis functions of 5 order in the non-polynomial space{1，t，sint，cost，sin2t}are constructed.They share the most properties with Bernstein basis，such as non-negative，normative，symmetry，and endpoints nature.The Bézier-type curve of 5 order based on the new basis functions have similar properties as the Bézier curve，such as convex hull，symmetry，geometric invariance and endpoint interpolation and end edge tangent property.C1andG1link conditions of the curve and an example in surface of revolution modeling are presented.The result of experimentation shows that the modeling method is effective and enriches modeling theories.

Bézier-type of 5 order basis;Bézier-type of 5 order curve;link;quadric curves;transcendental curves

TP391.72

：A

：1004-4329(2015)01-009-04

2014-10-20

安徽省高校优秀青年人才基金重点项目(2013SQRL113ZD)资助。

车 毅(1978－)，男，硕士，讲师。主要研究方向：CAGD，计算机图形学。