一类具有毒素和状态依赖时滞的离散种群模型的持久性

林雪如

(福州大学数学与计算机科学学院，福建福州 350116)

在文献[1]中，Chen 等研究了如下具有毒素和状态依赖时滞的种群模型

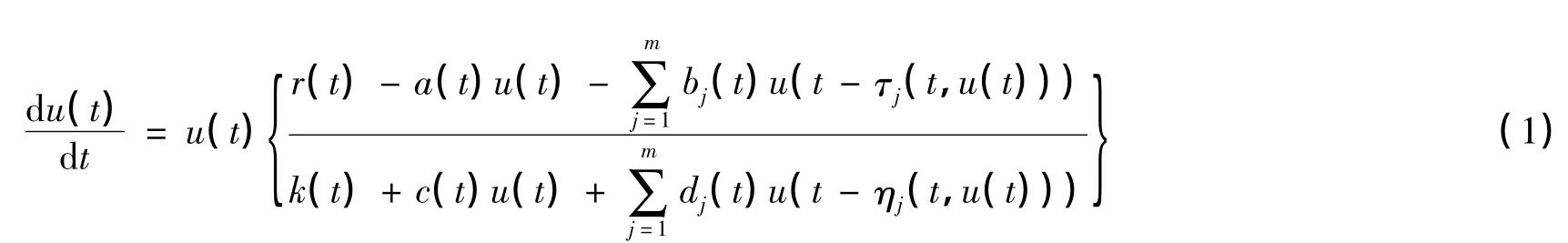
其中r(t)，k(t)，a(t)，c(t)，bj(t)，dj(t)，j= 1，2，．．．，m 都是非负连续的实值周期函数，而且具有周期ω ＞0 ; r(t)，k(t)，a(t)，c(t) ＞0 ;τj，ηj也为ω 周期函数。利用重合度理论，他们得到了系统(1)存在正周期解。关于系统(1) 的更多生态背景可以参见文献[1-4]以及它们所引用的文献。

然而，许多学者[5-11]提出: 当种群世代不重叠的时候，由差分方程描述的离散模型比连续模型更合适。而且，离散时间的模型可以为连续模型的数值模拟提供有效的计算模型，因此有必要研究用差分方程描述的离散时间模型。

众所周知，持久性是研究种群动力学行为的一个最重要的研究课题之一。数学生态学关注的最有趣的而且最有意义的问题是:生态种群模型中各个种群的生存性问题。从生物学的角度来看，一个系统中相互作用的物种在一个合适的环境条件之下是持久的，这意味着所有的种群将在长时间内永久持续生存下去。因此，很有必要研究一个生态种群系统在什么条件之下可以永久持续生存下去的问题。

基于上述问题的考虑，本文将研究系统(1) 对应的如下离散种群模型

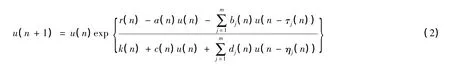
不像文献[1]中关于参数都是周期函数的假设，我们将考虑更一般的情形，即考虑系统是一般的非自治系统。因此，我们假设系统(2) 的系数满足如下条件:

r(n)，k(n)，a(n)，c(n)，bj(n)，dj(n)，τj(n)，ηj(n) ，j = 1，2，…，m 都是有界非负的序列。

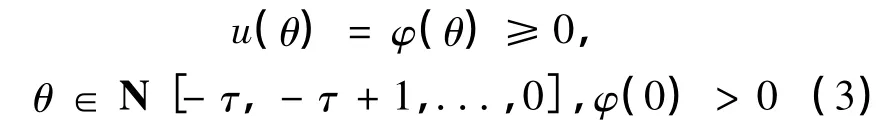
我们很容易可以得到，系统(2) 满足初始条件(3)的解u(n) ＞0，n ∈Z。

下面我们引入如下的记号:

对任意的有界序列 {a(n) }，

2 永久持续生存

定义1 如果存在正常数m 和M，使得系统(2)的每个正解u(n) 满足

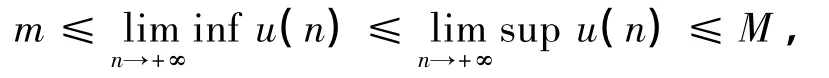
则系统(2)是永久持续生存的。

在这一节，我们将证明系统(2) 是永久持续生存的，在证明过程中需要用到一些引理。首先给出其中一个引理[12]。

引理1([12]) 令

如果y(k0) ≤u(k0)，那么y(k) ≤u(k) 对所有的k ≥k0成立。

接着，我们先来研究一下如下的单种群离散模型:

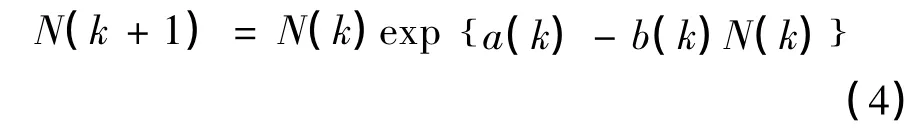
其中 {a(k) }和 {b(k) }都是严格正的有界实值序列，而且满足0 ＜al≤au，0 ＜bl≤bu． 类似于文献[6]中命题1 和命题3 的证明方法，我们很容易可以得到如下的引理:

引理2 对于系统(4) 满足初始条件N(0) ＞0 的任意解满足

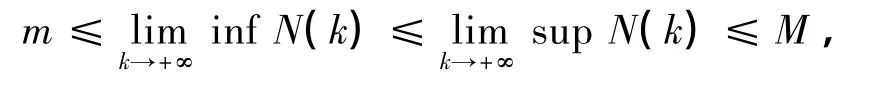
其中

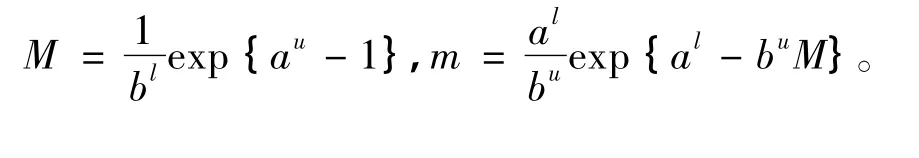
最后，我们给出证明系统(2) 是永久持续生存所需的第三个引理。

引理3([13]) 令x(n) 和b(n) 都是非负序列，c ≥0 是一个常数。如果

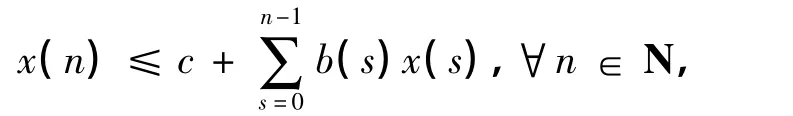
那么

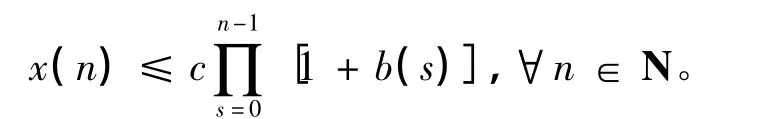
下面，我们将证明系统(2) 是永久持续生存的，首先给出如下的一个命题。

命题1 令u(n) 是系统(2)的任意一个正解，那么

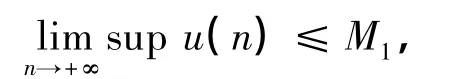
其中

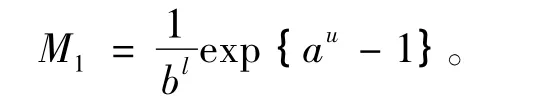
证明 令u(n) 是系统(2) 的任意一个正解，由系统(2)可以得到

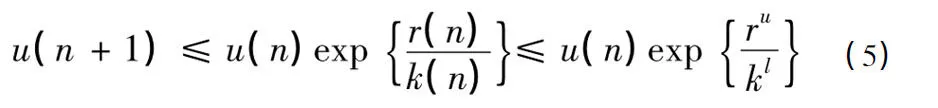
令u(n) = exp {x(n) }，那么

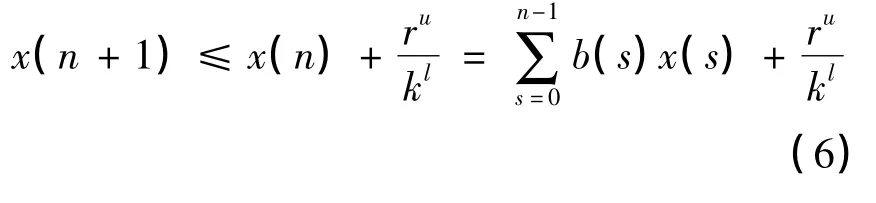
其中

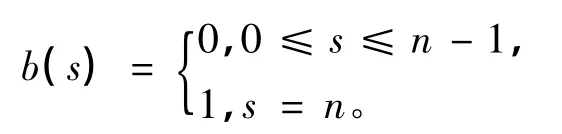
运用引理3，我们可以得到

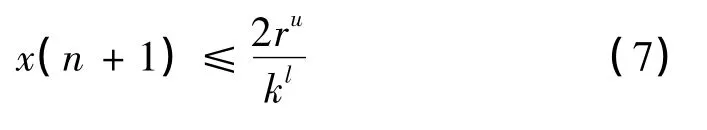
因此

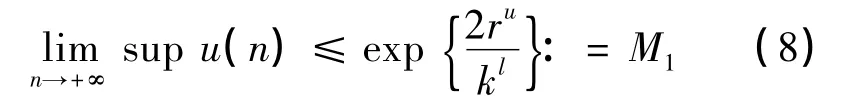
有了命题1，我们将给出系统(2) 是永久持续生存的结论。

定理1 假设

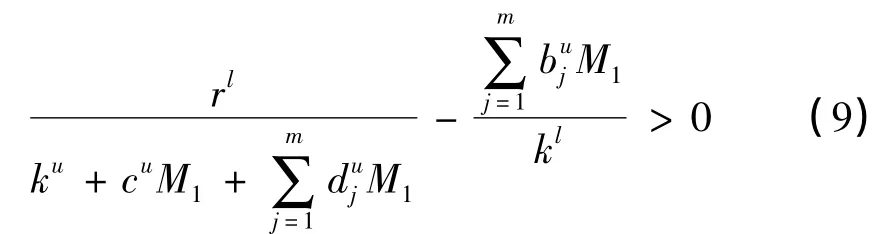
那么系统(2)是永久持续生存的。

证明 为了证明定理1，由命题1 可以知道，我们只需再证明在满足条件(9) 的前提之下，有，其中

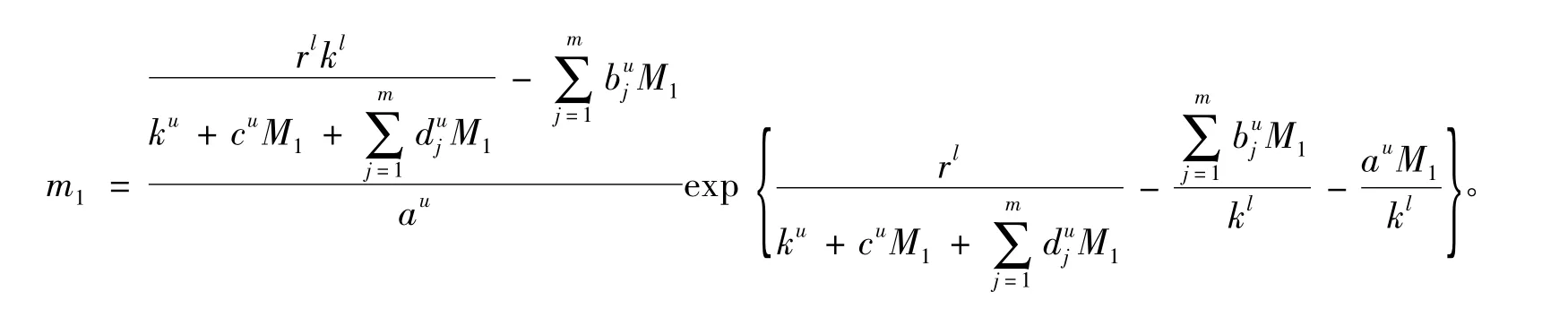
由命题1 可得，对任意的ε ＞0 ，存在正整数N1，当n ＞N1时，有

由系统(2)和(10)，我们可以得到

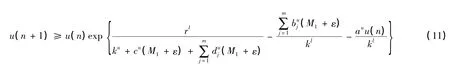
对任意的n ＞N1+ τ 成立。

由条件(9) 可知引理1 和引理2 可以应用到(11)，我们很容易可以得到

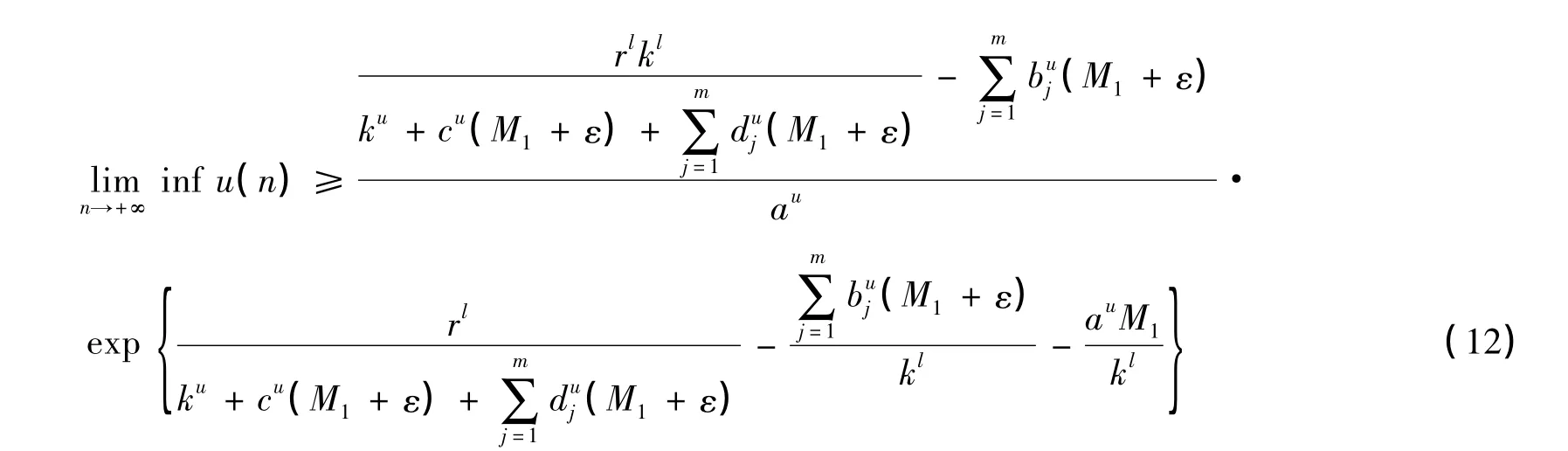
在(12)中令ε →0 ，可得

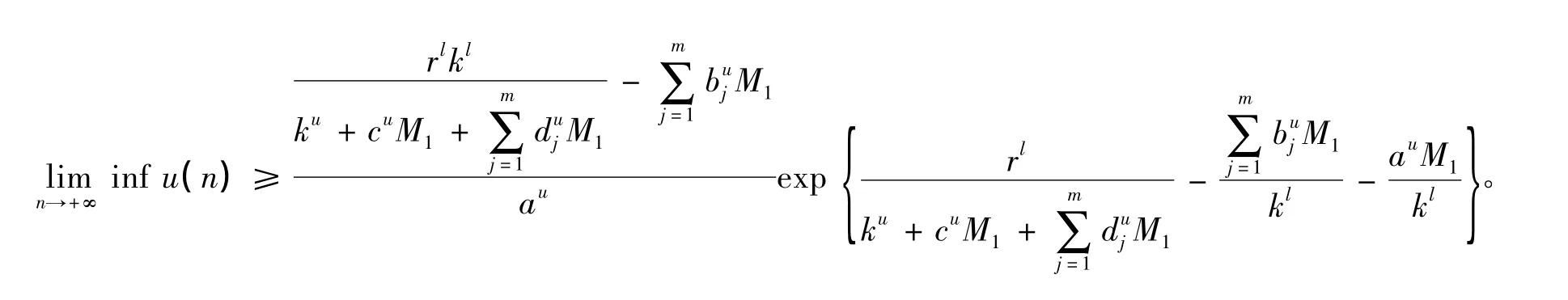
从而定理1 成立。

3 举例子

为了验证定理1 中条件的可行性，我们将举一个例子给予说明。

我们取r(n) = 0．5，k(n) = 2，a(n) = 1．2，c(n) = 0．001，m = 2 ，即考虑如下具有毒素和状态依赖时滞的种群模型:

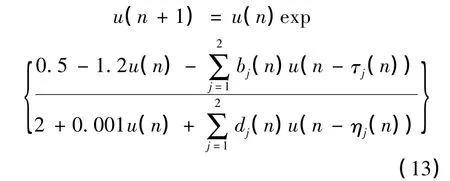
其中

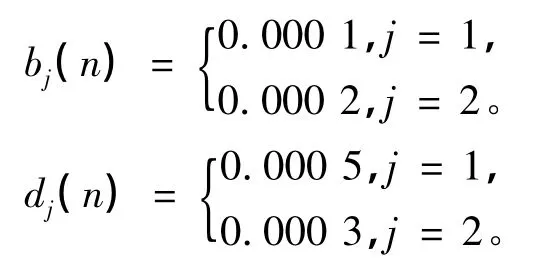
我们很容易验证定理1 中的条件满足，因此，由定理1 可以得到:系统(13)是永久持续生存的。

[1]Chen F D，Sun D X，Shi J L． Periodicity in a food-limited population model with toxicants and state dependent delays[J]． Journal of Mathematical Analysis and Applications，2003，288(1): 136-146．

[2]Fan M，Wang K． Periodicity in a food-limited population model with toxicants and time delays[J]． Acta Mathematicae Applicatae Sinica ( English Series)，2002，18 (2): 309-314．

[3]Li Y K，Kuang Y． Periodic solutions in periodic statedependent delay equations and population models[J]．Proceedings of the American Mathematical Society，2002，130 (5): 1345-1353．

[4]Feng W，Lu X． On diffusive population models with toxicants and time delays[J]． Journal of Mathematical Analysis and Applications，1999，233(1): 373-386．

[5]Agarwal R P． Difference Equations and Inequalities:Theory，Method and Applications[M]． New York :Monographs and Textbooks in Pure and Applied Mathematics，vol． 228，Marcel Dekker，2000．

[6]Chen F D． Permanence and global attractivity of a discrete multispecies Lotka-Volterra competition predatorprey systems[J]． Applied Mathematics and Computation，2006，182 (1): 3-12．

[7]Chen X X，Chen F D． Stable periodic solution of a discrete periodic Lotka-Volterra competition system with a feedback control[J]． Applied Mathematics and Computation，2006，181 (2): 1446-1454．

[8]Li Y K，Lu L H． Positive periodic solutions of discrete n-species food-chain systems[J]． Applied Mathematics and Computation，2005，167 (1) :324-344．

[9]Muroya Y． Persistence and global stability in Lotka-Volterra delay differential systems[J]． Applied Mathematics Letters，2014，17 (7): 795-800．

[10]Muroya Y． Partial survival and extinction of species in discrete nonautonomous Lotka-Volterra systems[J]．Tokyo Journal of Mathematics，2005，28 ( 1): 189-200．

[11]Yang X T． Uniform persistence and periodic solutions for a discrete predator-prey system with delays[J]．Journal of Mathematical Analysis and Applications，2006，316 (1) : 161-177．

[12]王 联，王慕秋． 常差分方程[M]． 新疆大学出版社，1991．

[13]Takeuchi Y． Global Dynamical Properties of Lotka-Volterra Systems[M]． World Scientific Press，1996．