分裂广义均衡问题及其收敛算法

陈玉清，黄建华

(福州大学数学与计算机科学学院，福建福州 350116)

0 引言

设E1和E2是两个实的Banach空间，C和Q分别是E1和E2的两个非空闭凸子集．设f:C×C→R，g:Q×Q→R是二元泛函，A:E1→E2是有界线性算子，F:C→E1是α－逆强单调算子，S:Q→E2是β－逆强单调算子．所谓分裂广义均衡问题(SGEP)是求一x*∈C，使得，

且使得u*:=Ax*∈Q满足，

单独观察问题(1)，它是一个广义均衡问题．广义均衡问题是一个十分热点的问题，近年来，众多学者对其进行了大量的研究并取得了许多有意义的成果．而分裂广义均衡问题研究的是一个广义均衡问题的解在给定的有界算子下的像是另一个广义均衡问题的解．分裂可行问题(SFP)、分裂最优化问题、分裂变分不等式问题(SVIP)、分裂均衡问题(SEP)等都是分裂广义均衡问题的特殊情况．其中分裂可行问题可应用于图像修复、信号处理、强度调解放射性治疗(IMRT)模型中．分裂最优化问题可广泛应用于两个不同空间中的优化问题．

本文针对SGEP问题提出三种不同的算法，并证明由这些算法构造的迭代序列弱收敛或强收敛于分裂广义均衡问题的解．所得的结果推广了文［1］等相关结论．

1 预备知识

以下恒设H是一实的Hilbert空间，C是H之中非空的闭凸子集，分别用〈·，·〉和 ·表示H上的内积和范数，用N和R分别表示正整数集和实数集，“→”和“——w→”分别表示强收敛和弱收敛．

定义1 映像S:C→C称为非扩张的，如果 Sx－Sy≤ x－y，∀x，y∈C．记F(S)为S的不动点集，即F(S)={x∈C=S(x )}．

定义2 映像A:H→H称为逆强单调的，如果存在α＞0，使得易见，如果映像S是非扩张的，则I－S是－逆强单调的．

定义3 映像T:H→H称为稳定非扩张的(firmly nonexpansive)，如果∀x，y∈H有

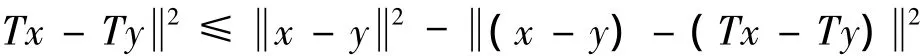
定义4 映像T:H→H称为稳定拟非扩张的(firmly quasi－nonexpansive)，如果∀x∈H，q∈F(T)有，Tx－q2≤ x－q2－ x－Tx2．

容易看出:1)T是稳定非扩张的⇔ Tx－Ty2≤〈Tx－Ty，x－y〉，∀x，y∈H;

2)如果T是稳定非扩张的，则T是非扩张的．

定义5 设C是H之一闭凸子集，f:C×C→R是一个二元泛函，假设f满足下列条件［2］:

(A1)对所有的x∈C，f(x，x)=0;

(A2)f是单调的，即，f(x，y)+f(y，x)≤0，∀x，y∈C;

(A4)对任意的x∈C，y|→f(x，y)是凸的和弱下半连续的．

引理1［3］设C是H之一闭凸子集，f:C×C→R为满足(A1)～(A4)的二元泛函，对r＞0及x∈H，定义映像Tfr:

1)Tfr是单值的;

2)Tfr是稳定非扩张的(firmly nonexpansive)，即，

3)F(Tfr)=EP(f);

4)EP(f)是闭凸的．

引理2［4］设C是H之一闭凸子集，且S:C→C是非扩张映像，则映像I－S在原点是半闭的．即{xn}⊂C，{xn}x，且xn－Sxn→0时，有x=S(x)．

引理3［5］设{xn}和{zn}是Banach空间E中的有界序列，{γn}⊂(0，1)且:0＜γn≤γn＜1．假设xn+1= γnxn+(1－γn)zn，n＞0以及(zn+1－zn－ xn+1－xn)≤0，那么zn－ xn=0．

自我是人性的必然组成部分，但是，这一代小孩为什么会唯我独尊到目空一切的程度呢？我想，很大原因就是，我们大部分家庭中，孩子的情绪、利益和需要都受到了父母的空前尊重。从小孩出生开始，就营造了一种氛围——孩子，你是家庭的核心，我们做的一切都是为了你。

一个Banach空间满足Opial条件，如果对X中的任意序列{xn}，xnx，则

任一Hilbert空间满足Opial条件．设H是一实的Hilbert空间，则任给x，y∈H，有

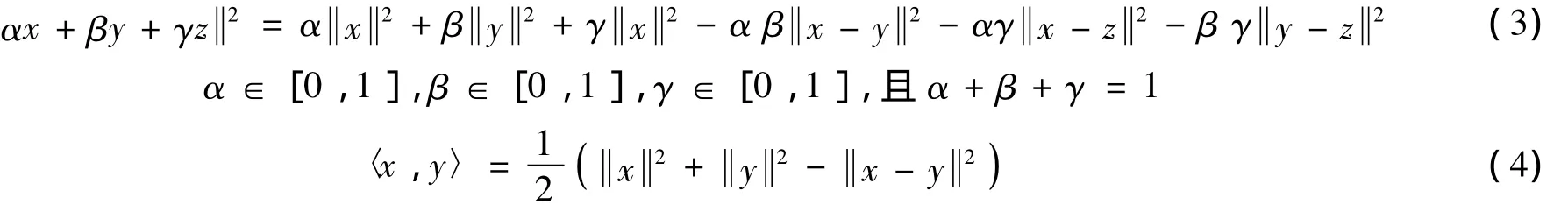
2 主要结果

条件1 设H1和H2是两个实的Hilbert空间，C和Q分别是H1和H2的两个非空闭凸子集．设f:C×C→R，g:Q×Q→R满足条件(A1)～(A4)，A:H1→H2为有界线性算子．假设F:C→H1为α－逆强单调算子，S:Q→H2为β－逆强单调算子．

记U=Tfr(I－r FPC)，T=Tgr(I－r SPQ)，r∈(0，a)，a=min{2α，2β，1}，μ∈(0，1/L)，L是算子A*A的谱半径，A*是A的共轭算子．

算法1 任给初始点

算法2 任给初始点x1∈C，αk∈(0，1)．

算法3 任给初始点

其中

定理1 在条件1下，如果Ω:={x∈EP(f，F)，Ax∈EP(g，S)}≠φ．那么由算法1产生的序列{xk}弱收敛于Ω中某一点x*．

证明 由引理1关于Tf

r的定义可知:对r＞0及x∈H．

因此 EP(f，F)=F(Tfr(I－rF )) ，同理可知EP(g，S)=F(Tgr(I－rS )) ．类似的，对r＞0及x∈H，

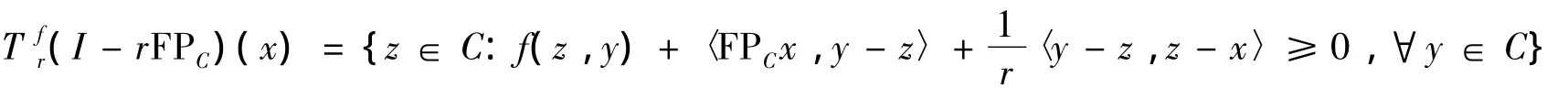
设z∈Ω，则z∈EP(f，F)且Az∈EP(g，S)，z∈C，Az∈Q那么

对任意的x，y∈C，由F是α－逆强单调的、r∈(0，a)知:

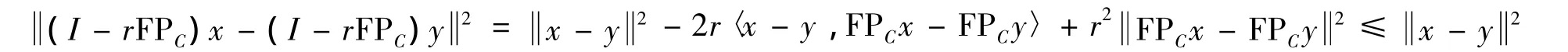
故I－r FPC是非扩张的，同理可证I－r SPQ是非扩张的，从而U、T也都是非扩张映像．由算法1可得:

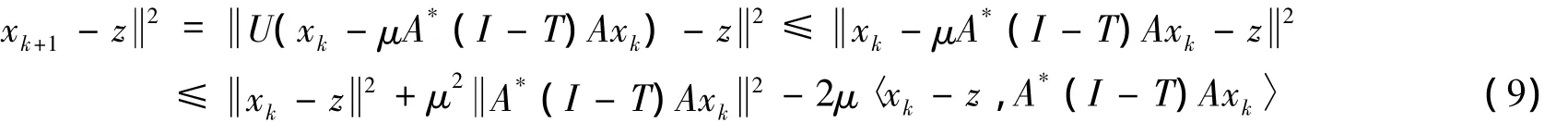
由式(4)、(8)及T是非扩张的知:

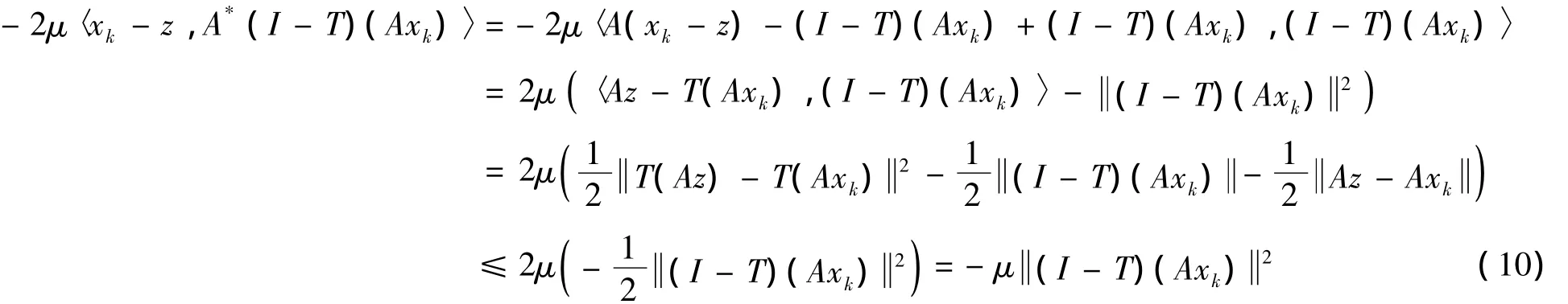
又因

结合式(10)～(11)，可得:因为μ∈(0，1/L)，所以 xk+1－z2≤ xk－z2，于是xk－z 存在．

令 uk=xk－ μA*(I－T)Axk，则 ukj=xkj－ μA*(I－T)Axkj．因为 xkjx*，所以ukjx*．

下面证明x*∈EP(f，F)．若x*∉EP(f，F)，则x*≠ Tfr(I－rF)x*，由于x*∈C故x*≠Tfr(I－r FPC)x*，因此Ux*≠x*．因U是非扩张的，故U－I是半闭的，所以

于是，存在某个ε＞0及{ukj}的子列{ukjs}使得对所有的s≥0，有 Uukjs－ukjs＞ε．

由于U是稳定非扩张的，又因z∈F(U)，故

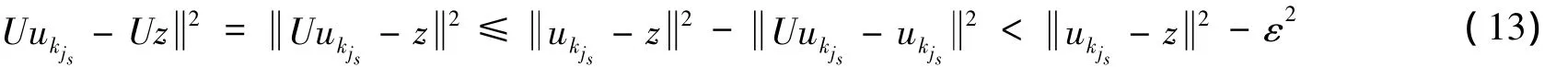
同时由式(9)～(12)知 xk+1－z≤ xk－μA*(I－T)Axk－z= uk－z≤ xk－z．根据式(13)有，

从上式我们得出 {ukjs－z }是单调递减的，故ukjs－z存在．另一方面，由式(13)～(14)知ukj－z2＜ ukjss+1－z－ε2，故存在矛盾，假设不成立，即x*∈EP(f，F)，所以x*∈Ω．

下证xkx*，假设存在{xk}的子列{xks}，使得xksp，且x*≠p．则根据Opial条件有，

矛盾．因此x*=p，所以{xk}弱收敛于x*∈Ω．定理得证．

收敛于某一点x*∈Ω．为证明定理2，我们先证明下面的引理．

引理4 定理2中的U［I－μA*(I－T)A］是非扩张映像．

证明 由于T是非扩张的，

因T是非扩张的，故I－T是1－逆强单调的，因此2

联立式(15)～(16)知:

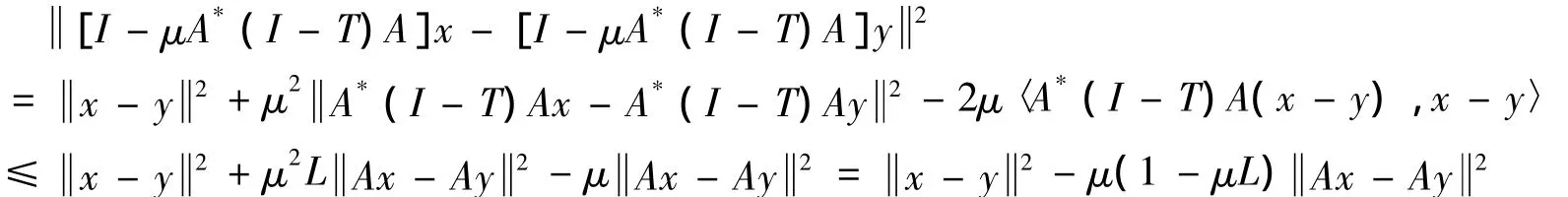
因μ∈(0，1/L)，所以 ［I－μA*(I－T)A］x－［I－μA*(I－T)A］y2≤ x－y2．所以I－μA*(IT)A是非扩张的，又因U是非扩张的，故U［I－μA*(I－T)］A是非扩张映像．

定理2的证明:设z∈Ω，则z∈EP(f，F)且Az∈EP(g，S)．由式(8)知z=Uz且Az=T(Az)．从而根据式(3)以及U非扩张知:

由式(10)～(11)可得式(17)等价于下面的式子:

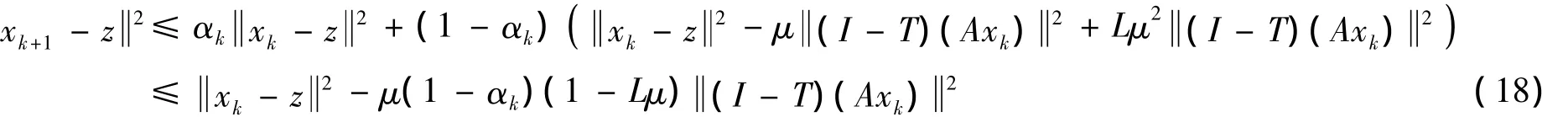
故 xk+1－z2≤ xk－z2，所以xk－z存在．又由式(18)可得，

令zk=U(xk－μA*(I－T)Axk)，uk=xk－μA*(I－T)Axk，由式(17)～(18)知:

另外由式(3)有，

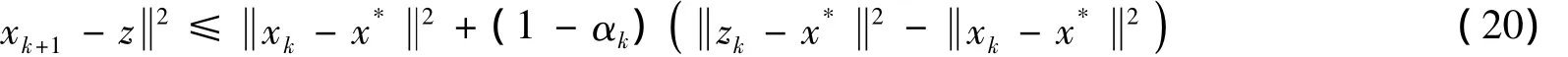
从而根据式(19)～(20)得知:0≤(1－αk)( xk－z2－ zk－z2)≤ xk－z2－ xk+1－z2．

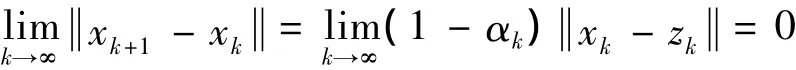
所以序列{xk}是Cauchy列，设xk→x*．易得T(Ax*)=Ax*，Ax*∈EP(g，S)．

下面证明x*∈EP(f，F)．若x*∉EP(f，F)，类似于定理1可知存在某个ε＞0及{uk}的子列{ukj}使得对所有的s≥0有

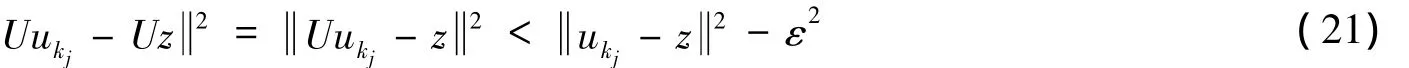
由 xk+1－z2≤ xk－z2及式(20)、(21)、(4)可得:

定理3 在条件1下，假设Ω:={x∈EP(f，F)，Ax∈EP(g，S)}≠φ．序列{xk}由算法3产生，且 {αk}⊂ (0，1)，{βk}⊂ (0，1)，{γk}⊂(0，1)满足:

证明 设z∈Ω，则z∈EP(f，F)且Az∈EP(g，S)．由式(8)知z=Uz且Az=T(Az)．令zk=

因此由式(3)、(23)知:

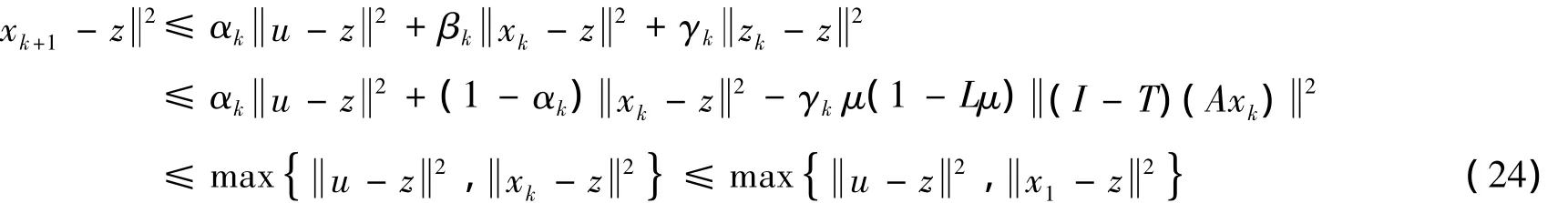
于是序列{xk}有界，序列{zk}、{uk}也是有界的．

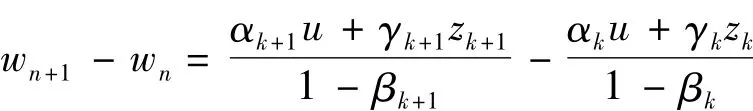
又因U是非扩张的，即得:

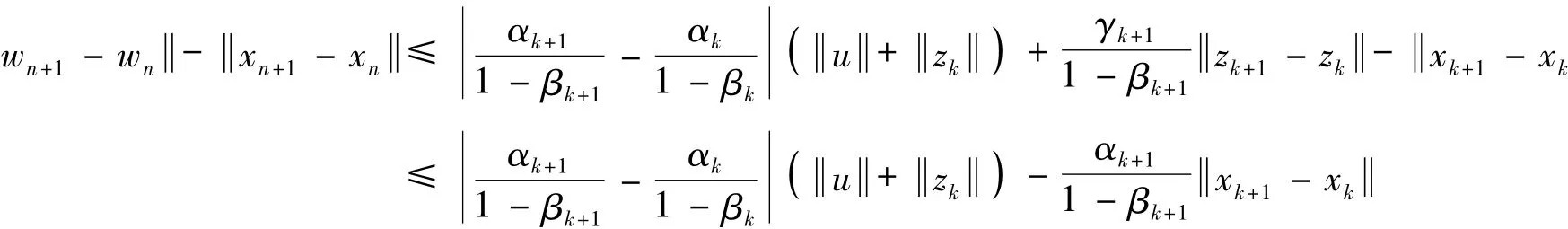
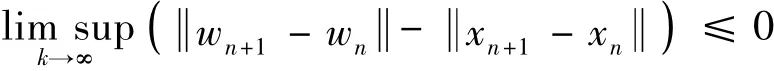
T gr(I－r SPQ)Ax*=Tgr(I－rS)Ax*，所以Ax*∈EP(g，S)．

下面证明x*∈EP(f，F)．若x*∉EP(f，F)，类似于定理1可知，存在某个ε＞0及{uk}的子列{ukj}使得对所有的s≥0有

于是根据式(23)、(25)可得:

例1 设E1=E2=R，C=［2，+∞)，Q=［6，+∞)．假设Ax=3x，Fx=2x，Su=2u以及f(x，y)=2(y－x)，g(u，v)=v－u，则问题(1)和(2)可分别重写为2(y－x)+2x(y－x)≥0和v－u+2u(vu)≥0，容易看出EP(f，F)={2}，且A(2)=6∈EP(g，S)，所以2∈Ω．

［1］He Zhenhua．The split equilibrium problem and its convergence algorithms［EB/OL］．［2012 －07 －20］．http://www．journalofinequalitiesandapplications．com/content/2012/1/162．

［2］Blum E，Oettli W．From optimization and variational inequalities to equilibrium problems［J］．Studia Mathematica，1994，63:123－145．

［3］Combettes PL，Hirstoaga A．Equilibrium programming in Hilbert spaces［J］．Journal of Nonlinear and Convex Analysis，2005，6:117－136．

［4］Marino G，Xu Hongkun ．Weak and strong convergence theorems for strict pseudo－ contractions in Hilbert spaces［J］．Journal of Mathematical Analysis and Applications，2007，329(1):336－346．

［5］Suzuki T．Strong convergence of Krasnoselskii and Mann’s type sequences for one parameter nonexpansive semigroups without Bochner integral［J］．Journal of Mathematical Analysis and Applications，2005，305:227 －239．