求解可分离凸优化问题的非精确混合分裂算法

曾玉华，杨 赟，彭 拯

(1．湖南大学数学与计量经济学院，湖南长沙 410082;2．湖南第一师范学院数学与计算科学学院，湖南长沙 410025;3．福州大学数学与计算机科学学院，福建福州 350116)

0 引言

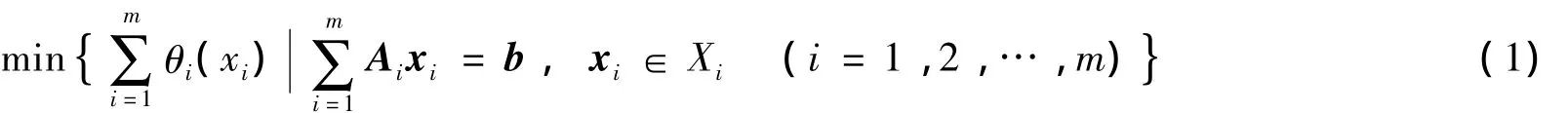
形如的优化问题被称为线性约束结构凸优化问题，其中θi(xi)为闭凸集Xi上的凸函数．

当m=1时，问题(1)就是一般线性约束凸优化问题，增广Lagrangian算法［1］和临近点收缩算法［2］等经典算法可用于求解此类问题．当m≥2时，问题(1)有着许多实际应用，如信号处理［3］，图像恢复［4］，统计学习［5］，等等．正是由于这些应用，国内外学者研究了当m=2，3时可分离结构凸优化问题的求解算法，算子分裂方法是求解这类问题最有效算法之一．算子分裂算法包括交替方向法和平行分裂算法．交替方向法最早可以追溯到Gabay［6］，当m=2时，交替方向法能够快速有效地求解问题(1);当m ＞2时，交替方向法的收敛性无法得到保证，见He等［7］．为此，He［8］提出了一种平行分裂增广Lagrangian算法，该方法是一种基于预测－校正的收缩算法，能够很好地拓展到求解m＞2且具有可分离结构的凸优化问题．结合交替方向法和平行分裂算法，许多学者针对问题(1)提出了多种分裂算法，如He等［9］通过在子问题的增广拉格朗日函数上增加临近点项，并线性化增广拉格朗日函数，提出了临近点交替方向法及三种线性化临近点交替方向法，该方法达到了简化子问题的作用;Han等［10］给出了一种临近点平行分裂算法;最近，He等［11］利用分块性质提出了一种Block－Wise交替方向法．

本文研究当m=4时，问题(1)的求解算法．即

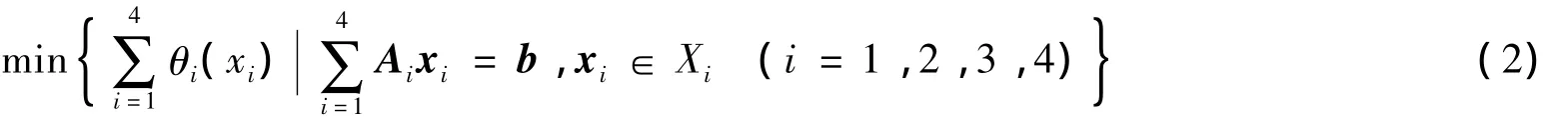
全文假设:

① Xi为 Rni(i=1，2，3，4)的简单闭凸集，且 n1+n2+n3+n4=n，Ai∈ Rm×ni;

②θi(xi)为Xi上的可微凸函数，记fi(xi)=▽θi(xi)，且fi(xi)在Xi上Lipschitz连续，即存在常数Lfi＞0，使得 fi(xi)－fi(x'i)≤Lfixi－x'i，∀xi，x'i∈Xi;

③问题(2)的解集非空．

本文提出一种非精确混合分裂算法求解问题(2)，该算法在每一轮迭代中求解四个子问题．依据计算工作量均衡的原则，算法将四个子问题平均分为两组，在每组内部执行平行分裂算法，两组之间执行交替方向算法．

1 预备知识及若干记号

其中

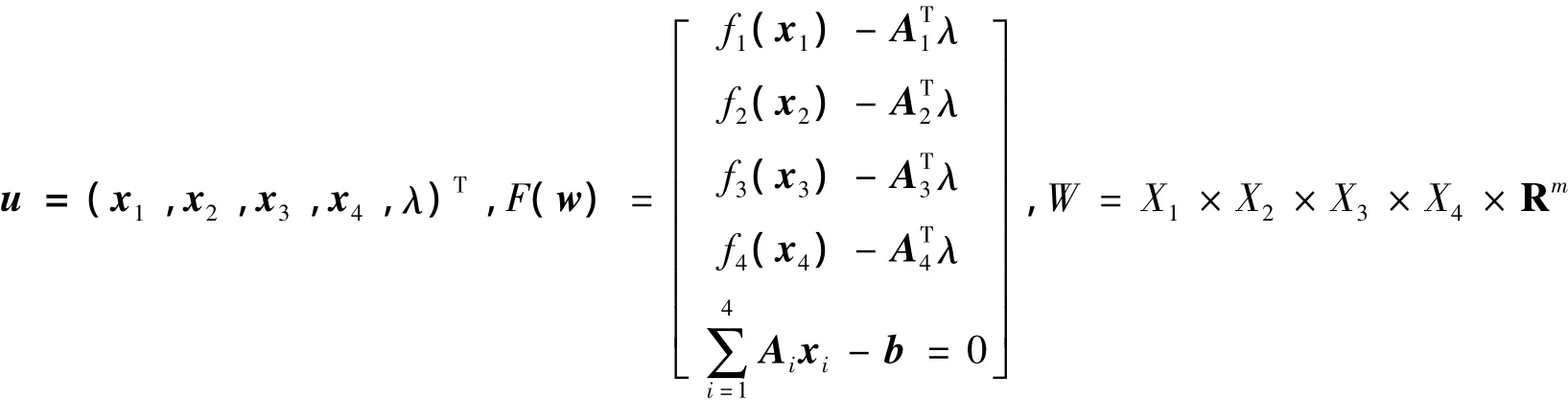
定义1 f:W→Rn是单调算子当且仅当

引理1 设W⊂Rn是闭凸集，PW(v)表示v在凸集W上的投影，则为了方便算法描述与收敛性分析，下列记号将被用到:H∈Sn++为对称正定矩阵，

2 算法描述

先给出求解问题(2)的非精确平行－交替混合算法，非精确混合分裂算法(HSM)．

S0:给定ε ＞ 0，r0＞ 0，ν∈(0，1)，γ∈(0，2)和矩阵H，迭代起始点w0=(x01，x02，x03，x04，λ0)∈Rn+m，令k=0．

且

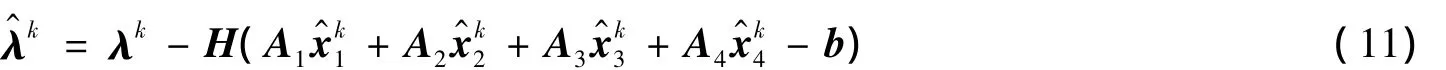
S2:产生迭代点，wk+1=(x1k+1，x2k+1，x3k+1，x4k+1，λk+1)，其中校正1

或者，校正2

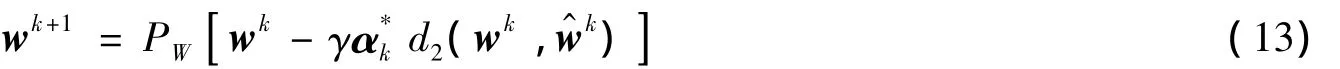
这里

注 在式(10)中，rk可通过自适应线搜索方法得到(参见文献［12］)，即定义

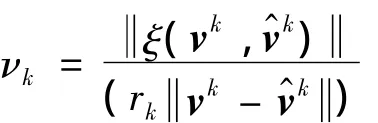
当νk＞ν时，rk:=rk×νk×1．25;当νk＜ν时，即为所要预测点．

由文献［12］可知，{rk}是非单调递减且有上界，即存在r0，使得

引理2 满足条件(10)的参数rk能在有限次循环得到．

证明 由式(4)的ξ(vk，)定义可知:

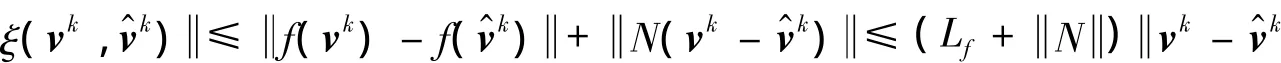
其中:Lf=max{Li:i=1，2，3，4}，因此，只要rk≥(Lf+N)ν，式(10)就成立，即有限次循环能使参数rk满足条件(10)．

引理3 若wk=，则为变分不等式VI(W，F)的解．

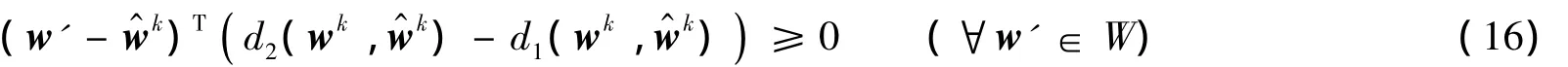
当 wk=时，d2(wk，)=F()，d1(wk，)=0．因此

3 收敛性分析

其中:

证明 由d1(wk，)的定义，结合条件(15)与Cauchy－Schwarz不等式，可得到 d1(wk，)的上界，具体计算过程从略．

定理1 存在一个α0＞0，使得α*k≥α0对于所有的迭代指标k成立，其中:α0=

其中:c=min{(1 － v)r0，0．5 H－1} ＞ 0．

证明 直接计算，并结合矩阵H的正定性，可得出结果。具体证明从略。

证明 由式(14)，(17)和(18)，结论显然成立．

引理6 对于任意的w*∈W*，由混合分裂算法(HSM)产生的序列{wk}满足

证明 由假设②可知，fi为单调函数(参见文献［13］)，因此F(w)为单调，所以

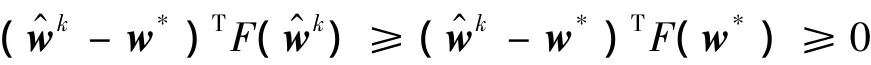
引理7 对于任意的w*∈W*，由混合分裂算法(HSM)产生的序列{w^k}，{wk}满足

证明 由于w*，wk∈W，令w'=w*，w'=wk，(16)可转化为

以上两式分别加上式(19)，可得

定理2 序列{wk}由混合分裂算法(HSM)的校正1产生，w*∈W*，那么

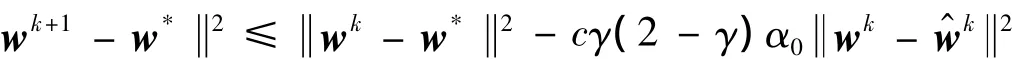
证明 由式(12)可知:

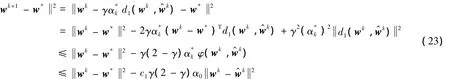
上式中第一个不等式由式(14)和(20)可得，第二个不等式由式(17)和定理1可得．定理得证．

定理3 序列{wk}由混合分裂算法(HSM)的校正2产生，w*∈W*，那么

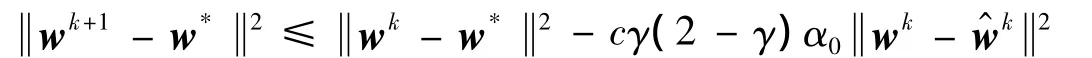
证明 由式(3)和(20)的第二个式子可知

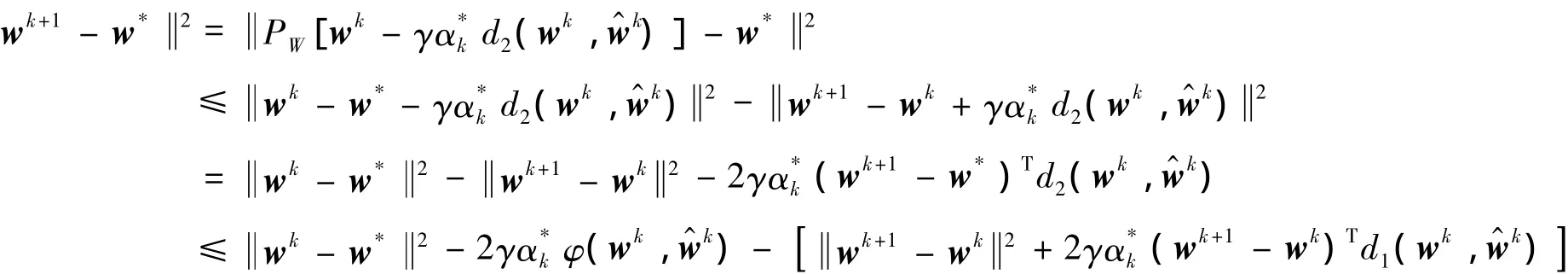
因为

结合式(14)，(17)和(19)，可得

定理4 设w∞为VI(W，F)的一个解．由混合分裂算法(HSM)产生的迭代序列{wk}收敛于VI(W，F)的一个解．

证明 该定理证明类似于文献［10］．

4 结论

针对一类带有四个可分离块变量的凸优化问题，提出一种基于分组的非精确混合分裂算法，即非精确两两平行－交替混合分裂算法(HSM)．该算法依据子问题计算工作量将子问题分为两组．每一组包含两个子问题，按照平行分裂算法的迭代格式来求解．两组之间按照交替方向算法的迭代格式求解．该算法在一定条件下可以看作分块乘子交替方向算法［11］的一种特例．算法允许子问题非精确求解，本文证明了非精确混合分裂算法的全局收敛性．与已有的分裂方法相比较，本文所提出算法由于允许非精确求解子问题，从而更具有实用性．同时，组间的交替方向法能够有效地提高实际收敛速度．

［1］Nocedal J，Wright SJ．Numerical optimization［M］．2nd．［s．l．］:Springer，1999．

［2］He Bingsheng，Yuan Xiaoming．A contraction method with implementable proximal regularization for linearly constrained convex programming［EB/OL］．［2011 －02 －21］．http://www．optimization － online．org/DB_HTML//2010/11/2817．html．

［3］Chen SS，Donoho D L，Saunders M A．Atomic decomposition by basis pursuit［J］．SIAM Journal on Scientific Computing，1998，20(1):33－61．

［4］Ng M，Weiss X M，Yuan Xiaoming．Solving constrained total－variation image restoration and reconstruct－ion problems via alternating direction methods［J］．SIAM Journal on Scientific Computing，2010，32(5):2 710 －2 736．

［5］Stephen B，Parikh N，Chu E，et al．Distributed optimization and statistical learning via the alternating direction method of multipliers［J］．Foundations and Trends in Machine Learning，2011，3(1):1 －122．

［6］Gabay D，Mercier B．A dual algorithm for the solution of nonlinear variational problems via finite element approxim －ation［J］．Computers＆ Mathematics with Applications，1976，2(1):17－40．

［7］Chen Caihua，He Bingsheng，Ye Yinyu，et al．The direct extension of ADMM for multi－ block convex minimization problems is not necessarily convergent［EB/OL］．［2013 －12 －01］．http://www．optimization － online．org/DB_FILE/2013/09/4059．pdf．

［8］He Bingsheng．Parallel splitting augmented Lagrangian methods for monotone structured variational inequalities［J］．Computation Optimization and Applications，2009，42(2):195－212．

［9］He Bongsheng，Peng Zheng，Wang Xiangfeng．Proximal alternating direction －based contraction methods for separable linearly constrained convex optimization［J］．Frontiers of Mathematics in China，2011，6(1):79－114．

［10］Han Deren，He Hongjing，Xu Lingling．A proximal parallel splitting method for minimizing sum of convex functions with linear constraints［J］．Journal of Computational and Applied Mathematics，2014，256(1):36 －51．

［11］He Bingsheng，Yuan Xiaoming．Block－wise alternating direction method of multipliers for multiple－block convex programming and beyond［EB/OL］．［2014－08－24］．http://www．math．hkbu．edu．hk/～xmyuan/Paper/Two－Group－ADMM －HY － Aug12．pdf．

［12］He Bingsheng，Liao Lizhi，Qian Maijian．Alternating projection based prediction －correction methods for structured variational inequalities［J］．Journal of Computational Mathematics，2006，24(6):693 －710．

［13］Fletcher R．Practical methods of optimization［M］．2nd．［s．l．］:John Wiley ＆ Sons，2013．