收发件同步的快递服务网点选址与车辆线路规划算法研究

黄丽君，郭昆

(1．福建工程学院管理学院，福建福州 350108;2．福州大学数学与计算机科学学院，福建福州 350116)

0 引言

在物流行业中，合理有效地安排快递服务网点、规划运输车辆的收件及发件线路，不仅是快递企业提高资源利用率、降低经营成本的重要目标，也对提高客户满意率、促进区域经济的发展都具有重要作用．物流网点的选址和车辆线路规划问题(location and routing problem，LRP)是NP完全问题［1］，精确求解方法只适用于小规模的物流网络．大规模LRP问题一般通过近似计算方法求解．近年来，针对快递业的物流优化问题，已有不少学者进行了相关研究．黄宇等［2］根据快递库存控制模型建立了多种物流配送成本模型，并对配送成本和配送周期等指标进行了定量分析．Kuo等［3］引入模糊决策方法寻求物流网点的最优选址问题．谷淑娟等［4］针对选址区域离散化问题提出基于多尺度网络模型的选址区域离散化方法．戢晓峰等［5］以移动仓库建设规模最小化为目标，提出基于多粒度集覆盖的蚁群算法．张玉环［6］在考虑配送时效性和逆向物流的基础上建立多级配送中心布局模型，并应用离散粒子群算法求解该模型．现有的研究主要集中于向客户发件的正向物流的优化，较少关注从客户收件的逆向物流(reverse logistics，RL)的优化．实际上，对于快递行业来说，如果能够将正向的发件网络与逆向的收件网络相结合，不仅能极大节约物流成本，也有利于提升客户服务的效率和质量．

群体智能进化算法是随机最优化算法的一个重要分支，主要通过模仿现实世界真实生物群落(如鱼群、蚁群等)的行为在问题的解空间中搜索接近全局最优解的最佳近似解．2000年，Tereshko等［7］提出了一种基于蜜蜂群体采蜜行为的蜂群算法．Karboga等［8］于2005年提出了更完善的人工蜂群算法(artificial bee colony，ABC)．ABC算法较好地挖掘了随机性探索能力强的优点并控制其易陷入局部最优解的缺点，从而逐渐成为蜂群算法的典型代表［9－12］．

针对快递企业的网点选址与线路规划问题(express location and routing problem，ELRP)，首先建立带有约束条件的问题数学模型，然后设计适应ELRP问题求解的离散ABC算法，最后通过算例验证算法的适应性和可靠性．

快递企业的物流配送网络通常可以分为收件网络和发件网络，需要设计两套互相独立的物流配送网点和配送车辆线路．在现实生活中，一个客户通常即有收件需求又有发件需求，造成两套网络存在大量重叠的线路．此时，可以考虑将收件网络和发件网络合并，建立一个统一的收发件同步的综合物流配送网络．合并之后的物流配送过程如图1所示．这样，车辆在向客户派发快递件的同时也同时从客户手里收取待发件，实现了服务网点、物流线路和车辆的充分利用，节省了物流运输和人工开支的成本．

图1 收发件同步的物流配送Fig．1 Concurrent send/receive logistics

1 ELRP问题建模

1．1 模型假设条件

①有若干地点供建立快递服务网点;②车辆的行驶线路为从服务网点出发，经过若干客户后再回到同一个服务网点;③车辆的总载货量能够保证完成所有客户的收件和发件的运输;④每辆车每趟只经过一个客户一次;⑤从客户至服务网点的运输成本只和运输路程的长短有关．

1．2 模型的参数及决策变量

模型参数:

Vr={ii=1，2，…，R}:R个用于建立服务网点的候选地点;Vc={ii=R+1，R+2，…，R+N}:N个待收发件的客户;S=Vr∪Vc:候选服务网点与客户的集合;Vv=∪Vvi，i=1，2，…，R:K辆运输车集合;Vvi={k服务网点i的客户由第k辆车服务，k∈{1，2，…，K}}，Vvi∩Vvj= Ø，i，j∈ Vr，i≠ j;Cri:在第i个候选地点建立服务网点的固定成本，i∈Vr;Cv:车辆单位距离运输成本;Cstore:单位货物在服务网点的存储成本;dsij:从地点i到地点j的距离，i，j∈S;Qv:车辆的最大载货量;Qri:服务网点i的最大库存量，i∈Vr;Qci，s:客户i平均发件量，i∈ Vc;Qci，r:客户i平均收件量，i∈ Vc．

决策变量:

1．3 数学模型

1)建立服务网点的固定成本:

2)为客户运输收发件的成本:

3)服务网点存储客户收发件的成本:

由公式(1)～(3)得到目标函数:

约束条件(5)保证每个客户的收发件只由一辆车来运输;约束条件(6)保证每辆车装载的物件都不大于其最大载货量;约束条件(7)保证每个服务网点存储的物件都不大于其最大库存量;约束条件(8)保证每辆车只为一个服务网点运输物件;约束条件(9)保证服务网点之间不存在直接的运输线路;约束条件(10)保证每个回收中心都有足够的车辆为其运输废弃物;约束条件(11)保证每辆车不会将废弃物运输到未建立回收中心的地点;约束条件(12)保证每条运输线路上经过的回收点均不存储废弃物;约束条件(13)保证每辆车的运输线路不会形成闭合的环;约束条件(14)和(15)保证决策变量为{0，1}变量．

2 EL RP模型的人工蜂群算法

2．1 标准ABC算法

标准ABC算法模拟自然界中蜜蜂群的采蜜过程求解连续目标函数的最优值［8］．食物源(food source)的花蜜丰度表达解的适应度．蜜蜂的角色分为觅食者(employed forager)、守望者(unemployed forager)、侦察者(scout)和追随者(onlooker)四种．算法的运行主要由觅食者和其追随者的觅食行为构成．追随者根据以下公式计算选择食物源的概率:

其中:fiti代表第i个食物源的花蜜丰度;SN为食物源数量．在觅食过程中，觅食者和它的追随者不会一直在同一个食物源采蜜，而是不断随机选择原有食物源附近的新位置尝试．新食物源的随机选择公式如下:

其中:k∈{1，…，SN}，j∈{1，…，D}为随机下标，且k≠j，D为解向量xi的维数;φij是［－1，1］上的随机实数．如果在新食物源的花蜜丰度更大，则按照贪心选择原则将xij替换为vij．

当一个食物源在一段时间内的花蜜丰度不再增加时，该食物源将被放弃．此时，一个原本留守在蜂巢的守望者被派出探索新的食物源，成为一个侦察者．新食物源的地点按如下公式计算:

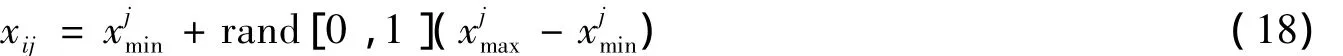
其中:xjmin和xjmax分别代表解向量xi的第j个分量的下限值和上限值;rand［0，1］代表［0，1］上的随机实数．

ABC算法需要设置的参数有:食物源数量SN;觅食者数量NP;最大迭代次数MCN和食物源被放弃前的尝试次数(limit)．不过，根据文献［9］的建议，NP通常可以与SN相等，limit可以设为SN×D．这样，标准ABC算法的参数可以减少到SN和MCN两个．

2．2 ELRP问题解的编码设计

ELRP问题解的编码如图2所示．X是一个R维二值向量，Xi=1表示在第i个候选地点建立快递服务网点;Y为K维10进制向量，Yi=j表示车辆i向服务网点j提供服务．借鉴文献［12］的思想，设计一个K×N的10进制矩阵Z．矩阵的每个行向量表示一辆车的行驶线路．矩阵元素Zij表示客户j是车辆i的行驶线路上的第Zij个节点．

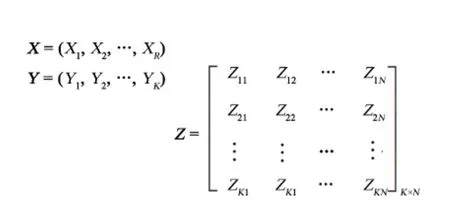
图2 ELRP问题解的编码方案Fig．2 Code design of the solution to ELRP

2．3 ELRP －ABC 算法

标准ABC算法是针对连续空间上的最优化问题设计的．当应用于离散空间上的最优化问题时，需要设计一种用整数表示实数的方案．这里，采用一种将实数四舍五入至最近整数的方法．相应地，式(17)和(18)变为

其中:vij∈［xjmin，xjmax］;round()为四舍五入函数．但是，这种扩展会遇到一个值域缩小的问题．具体来说，当分量vij的值超过阈值时，算法会将其替换为该分量允许的极限值，但这样可能会使其取值范围减小．例如:设xij=5，xkj=1，xjmin=0，xjmax=5，则vij的值域为1(当φj=－1时)至9(当φj=1时)．由于9大于xjmax，在将9替换为xjmax后，vij的值域将减小至［1，5］．值域的收缩会弱化在ABC算法中起核心作用的随机性，使算法的性能下降．为了解决这个问题，将公式(19)修改成如下所示的新公式:

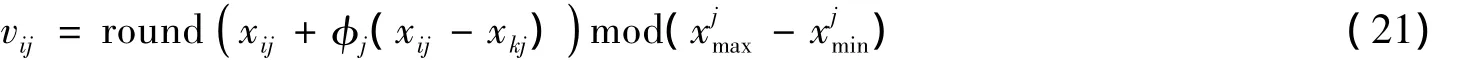
公式(21)中的取模运算用于在vij值到达一侧极限时翻转至另一侧极限．这样，就可以不需要检验vij是否超过其极限值，其值域即可保持不变．

算法的收敛速度是我们需要考虑的另一个问题．受算法在离散空间上的搜索速度快于连续空间及搜索步长的影响，ABC算法可能在MCN次迭代完成前已经达到收敛，从而造成多余的时间开销．一种常见的解决方案是引入一个稳定迭代参数StableIter．如果全局最优解在StableIter次迭代内无法改进，则算法即可结束．此外，为了保证算法搜索得到的解能够满足问题的所有约束条件，可以采用罚函数法对不满足约束条件的解进行惩罚，即通过在目标函数上乘以一个罚系数以降低解的适应度．在目标函数中添加一个罚系数后，新目标函数为:

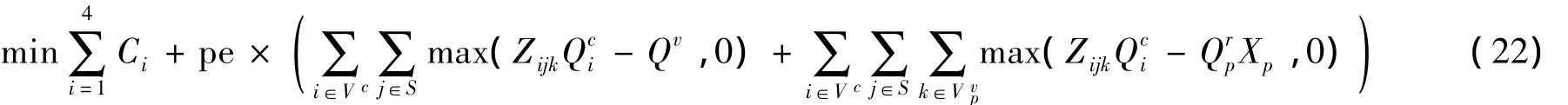
其中:罚系数pe为一个充分大的正实数，以惩罚违反约束条件(6)和(7)的解，增大其目标函数值，以降低解的适应度．这样，适应度降低的解在后续迭代中就会被逐渐淘汰．

综上所述，给出一个适用于ELRP问题的离散ABC算法(简称为ELRP－ABC算法)的具体步骤如下:

① 对ELRP问题的解进行编码，初始化解集xi，i=1，2，…，SN;②求每个解的适应度;③cycle=1;④根据公式为每个觅食者生成新的解;⑤根据贪心选择原则更新解;⑥根据公式计算每个解的概率Pi;⑦根据公式为每个追随者生成新解;⑧根据贪心选择原则更新解;⑨确定侦察者放弃的解，并根据公式计算新解;⑩记忆当前全局最优解;○11 cycle=cycle+1;○12 若cycle=MCN或最优解在StableIter次迭代内未改进，则算法结束，否则返回步骤④．

3 实验结果及分析

为了验证ELRP－ABC算法的性能，在文献［13］提供的算例的基础上，针对ELRP问题的特性进行了补充和完善，设计了适用于ELRP问题的测试数据．候选快递服务网点的坐标、建设成本及各地点的最大库存量如表1所示．客户的坐标及发件和收件量如表2所示．其它输入参数如表3所示．

表1 候选服务网点坐标、建设成本及最大库存量Tab．1 The coordinates，construction cost and maximum storage of the candidate services tations

表2 客户坐标及平均发件和收件量Tab．2 The coordinates of the customers and their average sending/receiving quantities

表3 其它输入参数的值Tab．3 Value of other input parameters

将ELRP－ABC算法与基于相同罚函数公式的PSO算法［14］(以下简称为 ELRP－PSO算法)进行对比．ELRPABC算法的参数设置为:NP=20，SN=10，MCN=2 000，stableIter=50，limit=20．ELRP－PSO算法的参数设置为:ω的取值借鉴文献［15］的设计从0．95线性递减至0．4，c1=2．0，c2=2．0，n=20，maxIter=1 000，stableIter=50．实验取20次重复运行的结果，表4显示算法得到的全局适应度及对应的最优总成本．

由表4可知，ELRP－ABC算法得到的近似最优解的全局适应度的波动范围较大，但对应的最优总成本的变化范围却不大，且最优总成本的最小值远小于ELRP－PSO算法．这表明:一方面，ELRP－ABC算法具有较强的随机性，能够较好保持种群的多样性，从而可以在更大范围内搜索问题的可行解;另一方面，ELRP－ABC算法又能够快速发现并逼近近似全局最优解，且在搜索过程中始终保持对近似最优解的记忆，显示算法具有良好的稳定性．虽然ELRP－PSO算法的全局适应度的最大值和最小值总是优于EL－RP－ABC算法，但是对应的最优总成本却总是远大于ELRP－ABC算法得到的最优总成本．这反映了:相对于ABC算法，PSO算法在搜索最优解的过程中容易陷入局部最优解，且跳出局部最优解的能力较弱．此外，两个对比算法均基于罚函数法，ELRP－PSO算法得到的较大的最优总成本表明其得到的近似解可能不满足部分约束条件，导致其目标函数受惩罚系数影响而增加较多．

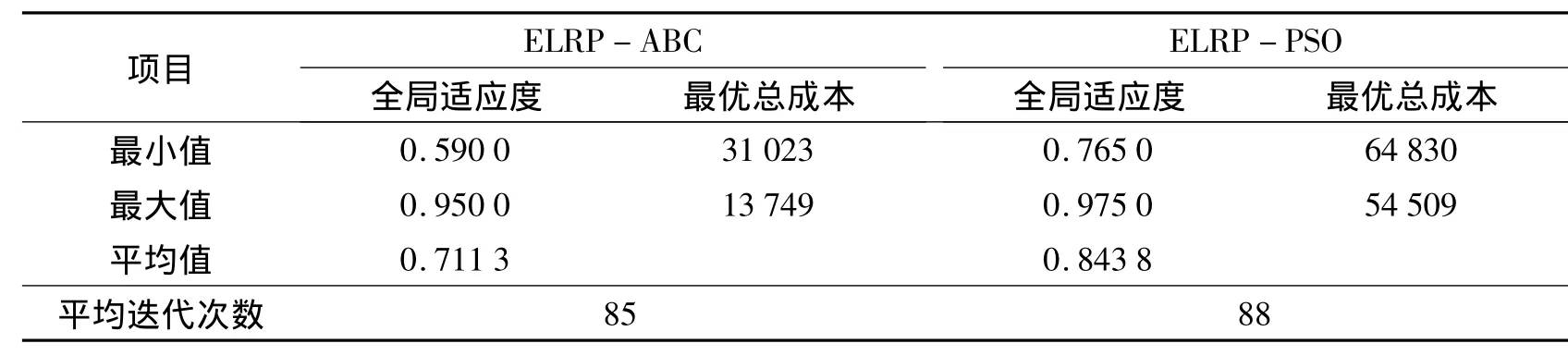
表4 ELRP－ABC算法与ELRP－PSO算法的实验结果对比Tab．4 Experimental results of the ELRP －ABC algorithm and the ELRP －PSO algorithm

4 结语

针对快递企业物流配送网络中的服务网点选址及运输车辆线路规划问题，建立了包含符指定合双向物流约束条件的数学模型，并针对该模型设计了一种新的基于离散ABC算法搜索全局近似最优解的方案．通过实际算例验证了提出的方法不但具有较高的搜索效率，而且得到的近似解具有较高的质量和稳定性．下一步将从改进ELRP问题的约束条件以更好地适应实际应用和设计具有更高效率的群智能进化算法等方面展开更深入的研究工作．

［1］Salman A，Ahmad I，Al－madani S．Particle swarm optimization for task assignment problem［J］．Microprocessors and Microsystems，2002，26(8):363 －371．

［2］黄宇．快递配送中心配送模型及应用研究［D］．长沙:长沙理工大学，2010．

［3］Kuo M S．Optimal location selection for an international distributioncenter by using a new hybridmethod［J］．Expert Systems with Applications，2011，38(6):7 208 －7 221．

［4］谷淑娟，高学东，刘燕驰，等．基于多尺度网格模型的物流配送中心选址候选集构建方法［J］．控制与决策，2011，26(8):1 141－1 146．

［5］戢晓峰，覃文文，焦新龙，等．高强度快递需求区域移动仓库选址算法［J］．交通运输工程学报，2012，12(6):69－75．

［6］张玉环．基于离散粒子群算法的快递公司城市多级配送网络布局优化［J］．商场现代化，2012(16):26－27．

［7］Tereshko V．Reaction － diffusion model of a honeybee colony’s foraging behavior［C］//Proceedings of the 6th International Conference on Parallel Problem Solving from Nature．San Francisco:［s．n．］，2000:807－816．

［8］Karaboga D．An idea based on honey bee swarm for numerical optimization［R］．Kayseri:Erciyes University，Engineering Faculty，Computer Engineering Department，2005．

［9］Karaboga D，Akay B．A comparative study of artificialbee colony algorithm［J］．Applied Mathematics and Computation，2009，214(1):108－132．

［10］Yeh W C，Hsieh T J．Artificial bee colony algorithm －neural networks for S－system models of biochemical networks approximation［J］．Neural Computing and Applications，2012，21(2):365 －375．

［11］Ravi V，Duraiswamy K．A novel power system stabilization usingartificial bee colony optimization［J］．European Journal of Scientific Research，2011，62(4):506 －517．

［12］Lei X，Tian J，Ge L ，et al．The clustering mode land algorithm of PPI network based on propagating mechanism of artificial bee colony［J］．Infor mation Sciences，2013，247:21 －39．

［13］董景峰，王刚，吕民，等．产品回收多级逆向物流网络优化设计模型［J］．计算机集成制造系统，2008，14(1):33－38;49．

［14］Kennedy J，Eberhart R C，Shi Y．Swarm intelligence［M］．San Fransisco:Morgan Kaufmann Publishers，2001．

［15］Shi Y，Eberhart R．A modified particle swarm optimizer［C］//Proceedings of IEEE World Congresson Computational Intelligence．Anchorage:IEEE Computer Society，1998:69 －73．