基于多目标遗传算法的无线传感器网络重新部署方法

邹长忠

(福州大学数学与计算机科学学院，福建福州 350116)

0 引言

无线传感器网络(WSNS)涉及众多学科，扩展了人们的信息获取能力，能够获取客观物理信息，具有广阔的应用前景．它主要由大量具有传感能力和计算能力、数据传输能力的小型传感节点构成．传感器网络部署问题是根据特定的要求，在给定的环境下，如何放置节点，达到预定的要求．其中很重要的一个指标就是覆盖度．覆盖可以有区域覆盖、点集覆盖、栅栏覆盖．部署方面根据目标区域是否可以靠近，分为决定性部署和随机性部署．但是在环境恶劣地方，如高原、雪山，或者要部署在敌区附近等这些人为不可能靠近的地方，只能采用随机部署方法，即通过空投等方式．这样必然造成节点分布不均，或者达不到任务要求．随着可移动节点的引入利用，可以在随机部署后，利用节点的移动来重新部署，达到预定的要求．文［1－5］利用虚拟合力算法，节点的移动依靠虚拟合力作用，节点沿合力方向虚拟移动，形成新的位置．文献［6－10］提出基于计算几何模型的节点部署方案．文［11］利用行列扫描法来均衡节点．文［12］将问题转化为最小成本最大流问题，通过求解此问题，实现对网络的优化部署．文［13］提出一种基于二部图匹配的重新部署算法，将初始网络描述成一个二部图，图的顶点集合由移动节点集合和需要覆盖的网格集合组成．如果某个移动节点可覆盖某个网格，则它们之间存在一条边，衡量移动的花费可使用移动的距离、消耗的能量或跳跃的次数等．对构造的二部图求其最小花费的最大匹配基，则该匹配基对应着一个最优的移动方案．文［14］提出结合虚拟合力和粒子群算法来优化网络覆盖．以上这些文献考虑的部署均为单目标，即部署后使得区域覆盖率最大化．文［15－21］提出多目标部署，文献考虑的因素一个是覆盖，另一个为网络生命期，还有的考虑所用节点个数．文［22］利用遗传算法，考虑区域覆盖率和节点的移动量，但是设定的场合是节点的移动量是固定的，且求解问题也是将多目标利用加权方式转为单目标，不能得到前沿解．

本文研究移动传感器网络，节点在随机部署后，考虑不同节点移动量不同，确定最小化最大节点移动量和最大化网络覆盖率的双目标前沿解．

1 网络模型

网络模型，目前传感器网络有三种感应模型:布尔、概率、信号强度．采用通用的布尔感应模型，即在检测区域内的任何一个点，若其位于任意一个传感器节点的感应半径为圆形的感应区内，则称该点被覆盖．假设考虑的场景为一个平面长方形区域A，该区域长、宽分别为L，W．随机空投n个网络节点，用(x0i，y0i)表示节点i的初始位置，(0≤x0i≤L，0≤y0i≤W)．如图1所示．

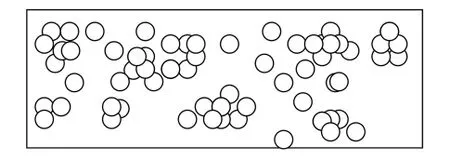
图1 区域A示意Fig．1 The detection area A

定义1 网络覆盖率．区域内的某点p，如果存在一个节点si，使得d(si，p)≤Rs，其中d(si，p)为节点si与p的距离，Rs为节点的感应半径，则称点p被覆盖．定义的网络覆盖率:

则计算:

定义2 节点移动量．节点i的当前位置为(xi，yi)，则节点i的当前移动量表示为:

我们的目标是整个区域的覆盖率要大，而所有节点中的最大移动量要最小．这两个目标是一对矛盾体，因为在初始随机部署后，要增加覆盖率，必然要移动节点，造成移动量增加．在极端情况下，所有节点在初始部署后不再移动，设节点是随机均匀地投入区域A，则区域中任意一点被覆盖的概率为:

2 多目标遗传算法基础理论

在给出具体的算法之前，先引用几个关于多目标优化Pareto解的基本定义．

定义3 多目标优化函数．设D⊂Rn，x∈D为变量，fi(x):D→Rm为目标函数，gi(x)，hj(x):D→Rm为约束条件．含约束多目标极小化函数可以定义为:

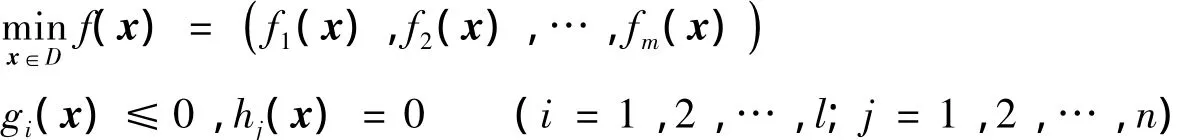
定义4 Pareto占优．若向量u=(u1，u2，…，un)与向量v=(v1，v2，…，vn)存在这样关系:∀i∈{1，2，…，n}，有 ui≤vi，并且至少∃i∈{1，2，…，n}，使得ui＜ vi，则称u比v占优，计为u≺v．

定义5 Pareto最优解．一个解x∈D是Pareto最优解，指不存在一个解x'∈D，使得f(x')≺f(x)．

3 多目标遗传算法的无线传感器网络部署

3．1 问题编码

用实数表示染色体编码，一个染色体即为一个可行解，表示n个传感器节点的当前位置，并假设每个节点有固定的ID，ID从1到n依次排列，Pi(xj，yj)表示第i染色体个体即第j个节点当前位置为(xj，yj)，见表1．

表1 染色体i表示Tab．1 Chromosome i

3．2 交叉和变异算子选择

交叉算法采用单点交叉操作，见表2、3．采用两两染色体随机组合进行交叉，生成新的两个染色体，采用虚拟合力算法，对染色体进行变异操作．

表2 单点交叉前Tab．2 Before single－point cross

表3 单点交叉后Tab．3 One－point crossover

变异操作:首先随机选取某些染色体，随机选取该染色体中某些个体，根据虚拟合力，确定这些个体节点的节点位置．

定义虚拟合力:

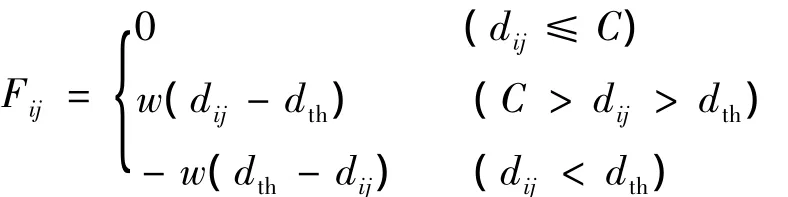
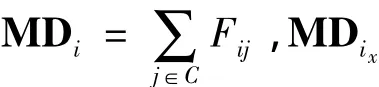
3．3 适应值函数

两个目标函数，max f1(x)=C(A)，min f2(x)=max dsi

3．4 算法

步骤1:初始化，产生一个大小为2 000的随机种群．

计算每个个体的覆盖率指标和最大移动距离．

步骤2:基于NSGA－II，做非占优排序，产生非占优前沿(F1，F2，…，Fr)．同一个级别的Fi做拥挤距离排序．

步骤3:按非占优排序和拥挤距离排序后，选取k个个体．

步骤4:根据虚拟合力的交叉和变异操作从P产生后代P'．对P'中每个个体计算C(x)和dsi．

步骤5:合并P=P∪P';

判断是否符合结束条件，若没有则转到第2步，否则结束．

4 仿真实验

在CPU为Intel i7－3537U处理器，3．1 GHz内存为4 G PC机上，通过matlab2012b平台实验．选取仿真区域为300 m×300 m的平面区，传感器感应半径为15 m，通信半径为20 m，随机部署节点数为80个．在相同的节点初始位置下，设定虚拟合力距离阈值为7．5 m．遗传算法变异概率若太大容易破坏种群的优良模式，若太小容易找到最优解，但是进化速度太慢．通过实验测试发现，设定遗传算法选取某染色体变异操作的概率为0．6，选取该染色体的某个体概率为0．2时，既能较好地保持上一代的占优解，又能防止算法过早地陷入局部最优解．分别设定种群大小为20，30和50．不同的种群大小下，得到的占优解分布图(种群数20，30，50)见图2，迭代800次．

从实验结果发现，当节点移动距离比较小时，随着移动量加大，网络覆盖率也明显提高．而节点移动距离较大时，网络覆盖率提高有限，这是因为这时节点之间基本上不存在重叠现象，节点的移动对提高覆盖率的作用很小．在与以上同样的仿真环境下，设定种群大小为50，分别在迭代次数为500，800，1 000次时得到的占优解情况如图3．本文算法与NSGA－II比较见图4．

图2 占优解(种群20)Fig．2 The dominant solution(population 20)

图3 不同的迭代次数，得到的占优解分布图(迭代次数:500，800，1 000)Fig．3 Different number of iterations，the resulting dominant solution(the number of iterations:500，800，1000)

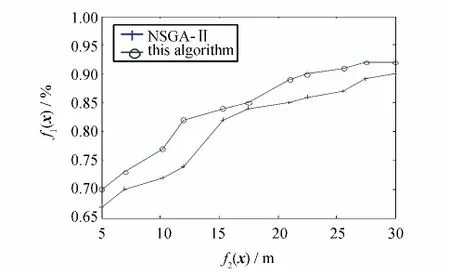
图4 本算法与NSGA－II比较Fig．4 This algorithm is compared with the NSGA －II algorithm

从图3可以看出，迭代次数越多，那么离最优解越近，这是由于遗传算法，采用保存当前占优解的结果．同样到后面，由于节点之间的重叠率很低，所以迭代后期效果不明显．

在同样的迭代次数和初始条件下，从图4可知，本算法得到的占优解比直接应用NSGA－II要好．主要是由于在节点的变异操作上采用基于虚拟合力算法，使得节点能往更多的空白方向移动，也即增大网络覆盖率方向移动，较快地接近实际最优解．

5 结语

在许多恶劣的情况下，传感器网络只能随机部署．本研究通过节点的动态移动来增强覆盖率，同时考虑节点的最大移动距离最小化．基于NSGA－II，利用选优和排序算法，引入虚拟合力对基因进行变异，达到网络覆盖率与节点移动距离之间的平衡，实验证明，结果能得到较分散的前沿占优解．

［1］Howard A，Mataric M J，Sukhatme G S．Mobile sensor network deployment using potential fields:a distributed，scalable solution to the area coverage problem［C］//Proc of the 6th Int Symposium on Distributed Autonomous Robotics Systems．Fukuoka:［s．n．］，2002:299 －308．

［2］Hussein I，Stipanovic D M．Effective coverage control for mobile sensor networks with guaranteed collision avoidance［J］．IEEE Transactions on Control Systems Technology，2007，15(4):642－657．

［3］Zou Y，Krishnendu C．Sensor deployment andtarget localization based on virtual forces［C］//Proc of 22nd Annual Joint Conf of the IEEE Computer and Communications．San francisco:［s．n．］，2003:1 293 －1 303．

［4］Heo N，Varshney P．Energy－efficient deployment of intelligent mobile sensor networks［J］．IEEE Trans on Systems，Man and Cybernetics，2005，35:78 －92．

［5］Ma K，Zhang Y，Trappe W．Managing the mobility of a mobile sensor network using network dynamics［J］．IEEE Trans on Parallel and Distributed Systems，2008，19(1):106－120．

［6］Wang G，Cao G，La Porta T F．Movement－ assisted sensor deployment［J］．IEEE Trans on Mobile Computing，2006，6:640－652．

［7］Ma M，Yang Y．Adaptive triangular deployment algorithm for unattended mobile sensor networks［J］．IEEE Trans on Computers，2007，56(7):946 －958．

［8］Bartolini N，Calamoneri T F，La Porta T，et al．Autonomous deployment of heterogeneous mobile sensors［C］//Proc of IEEE ICNP，Princeton，2009:753－766．

［9］Tan G，Jarvis S A，Kermarrec A M．Connectivity－guaranteedand obstacle－adaptive deployment schemes for mobile sensor networks［J］．IEEE Trans on Mobile Computing，2009，8(6):836 － 848．

［10］Hummel K A，Sterbenz J P G．Self－ organizing systems［M］//Bartolini N，Calamoneri T，Fusco E，et al．Autonomous deployment of self－ organizing mobile sensors for a complete coverage．Vienna:Springer Berlin Heidelberg，2008:194 －205．

［11］Wu J，Yang SH．Smart:a scan－based movement－assisted deployment method in wireless sensor networks［C］//IEEE Conf on Computer Communications．Miami，2005:2 313 －2 324．

［12］Chellappan S，Bai X L，Ma B，et al．Mobility limitedflip － based sensor network deployment［J］．IEEE Trans onParallel and Distributed Systems，2007，18(2):199 －211．

［13］Cui C，Shen Z，Chang Y L，et al．Movement－assisted sensor network deployment algorithm for maximizing the networkcoverage［J］．Jof Xidian University，2009，36(2):222 －227;284．

［14］Wang Xue ，Wang Sheng，Ma Junji．An improved co－ evolutionary particle swarm optimization for wireless sensor networks with dynamic deployment［J］．Sensor Network，2012，20(3):12 －20．

［15］Ferentinos K P，Tsiligiridis T A．Adaptive design optimiza － tion of wireless sensor networks using genetic algorithms［J］．Comput Netw，2007，51(4):1 031－1 051．

［16］Molina G，Alba E，Talbi E G．Optimal sensor network lay－out using multi－objective metaheuristics［J］．JUniv Comput Sci，2008，14，(15):2 549－2 565．

［17］Kang C，Chen J．An evolutionary approach for multi－ objective 3d differentiated sensor network deployment［C］//Proc IEEE Int Conf CSE’09．Vancouver，2009:187 －193．

［18］Jourdan D B，deWeck OL．Layout optimization for a wireless sensor network using a multi－objective genetic algorithm［C］//IEEE Veh Technol Conf P．Los Angeles，2004:2 466 －2 470．

［19］Jia J，Chen J，Chang G，et al．Multi－ objective optimization for coverage control in wireless sensor network with adjustable sensing radius［J］．Comput Math Appl，2009，57(11/12):1 767 －1 775．

［20］Jia J，Chen J，Chang G，et al．Energy efficient cover－ age control in wireless sensor networks based on multi－ objective genetic algorithm［J］．Comput Math Appl，2009，57(11/12):1 756 －1 766．

［21］Konstantinidis A，Yang K，Zhang Q，et al．A multi－objective evolutionary algorithm for the deployment and power assignment problem in wireless sensor networks［J］．Comput Netw，2010，54(6):960 －976．

［22］匡林爱，蔡自兴．基于遗传算法的无线传感器网络重新部署方法［J］．控制与决策，2010，25(9):1 329－1 332．

［23］Deb K，Pratap A，Agarwal A，et al．A fast and elitist multi－objective genetic algorithm:NSGA［J］．IEEE Trans on Evolutionary Computation，2002，6(2):182－197．