径流时间序列复杂网络的动力学拓扑性质

唐 强，胡铁松



径流时间序列复杂网络的动力学拓扑性质

唐 强1，胡铁松2

（1. 武汉纺织大学 数学与计算机学院，湖北 武汉 430200；2. 武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉 430072）

以金沙江和美国Ocumlgee河日径流序列为对象，利用复杂网络理论对径流序列的波动性特征进行了初步探讨。通过粗粒化方法将径流时间序列转化为符号序列，进而构建相应的复杂网络。对网络的聚类系数、平均路径长度和中介中心性测度等动力学统计特征量和拓扑参数的讨论发现，网络的聚类系数较大而平均路径长度较小，不同的波动模式之间存在着短程相关性；不同顶点的中介中心性测度具有明显的差异，表明某些顶点所代表的波动模式有着重要的意义，在一定程度上可以作为各种波动模式之间转换的前兆。这些结论有助于更好地把握径流变化的规律，对于径流的短期预测具有一定的参考价值。

径流序列；波动性；复杂网络；粗粒化；聚类系数；平均路径长度；中介中心性测度

径流过程是一种重要的水文现象，借助各种时间序列的分析方法研究径流序列的性质，提取所需信息，揭示其内在规律对于水资源的利用有着重要的意义，长期以来受到众多研究人员的重视。非线性科学的发展，为径流过程的定量分析与研究提供了新的理论和方法，人们利用混沌、分形和小波等非线性理论对径流序列进行了研究，试图解释序列波动的原因和机理，并对其未来的变化趋势做出预测，几十年来取得了丰硕的成果[1-6]。

由于河川径流受到自然环境、社会条件和人类活动多重制约，同时又存在着各种尺度关联和各种波动，具有高度的复杂性，需要利用多种方法，从不同的角度来进行讨论。上个世纪90年代兴起的复杂网络理论为径流过程的研究提供了一种新的思路[7-9]。

在本文中，我们以金沙江屏山站与佐治亚州Ocumlgee河Macon站日径流时间序列作为研究对象，首先运用等概率粗粒化方法，将径流序列转化为复杂网络，把径流序列波动信息编码在网络的拓扑结构之中；随后通过对网络的动力学统计特征量和拓扑参数等进行分析，获取径流波动网络的内在规律性，从复杂网络的角度解释径流变化的动力学特征。

1 径流时间序列的粗粒化处理

郝柏林提出可以通过符号动力学建立运动轨道和形式语言的联系，然后借助语法复杂性理论来刻画复杂性，其核心内容就是符号动力学与时间序列的粗粒化和符号化[10]。粗粒化常用的方法是对系统区间进行同质划分[11]，将整个区间分成有限个子区间。如果对划分后的每个子区间赋予一个符号，则整个系统区间就转换为一个符号序列，对粗粒化符号序列的研究也就是对相应时间序列的研究。由于粗粒化过程舍去了小层次上的细节，粗粒化形式的符号序列又具有有限性，这就使得粗粒化方法能突出系统的本质的特征。

粗粒化的精度对结论的有效性有很大的影响，这就要求在进行符号转换时，确定的符号种类不能太多，每一个符号要尽可能代表系统变化中的某一种基本的、相对独立的模式。常见的粗粒化方法有二值粗粒化、多值粗粒化和等概率粗粒化等方法[12, 13]。

多值粗粒化方法没有考虑不同的符号在符号序列中出现的概率，等概率粗粒化方法可以使得不同的符号在符号序列中出现的概率相同。记日径流序列为{(),=1,…,}，首先计算径流量的波动()：

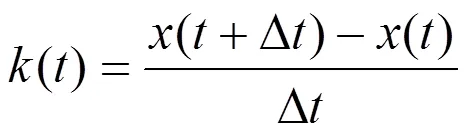
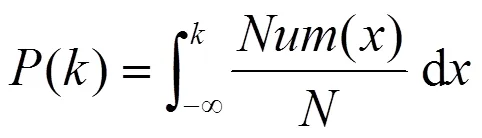
其中()为对应一种径流量波动模态发生的次数[13]。按照等概率的思想，我们将径流量的波动()分为4个区间，定义4个特征字符

其中，代表径流量快速增加，代表径流量缓慢增加，代表径流量缓慢降低，代表径流量快速降低。这样就可以将径流序列转化为符号序列：

2 复杂网络的构建

将时间序列粗粒化处理后，可以得到由4个字符{,,,}构成的符号序列。在符号序列中，称由个字符构成的字串为字串。理论上不同的字串共有4种。在符号序列的分析中，相互连接的字符的基本模式称为元结构。这些字串即为符号序列的元结构，代表了各种波动模式。符号序列表现了一种波动模式向另一种波动模式的转变，这种转变体现了各种波动模式之间的信息传递等关系，具有多元化的特征。后一个模式的出现是以前一个或多个模式为基础的，体现了一定的记忆性，因此模式之间的联系是“有向”的，联系的强弱程度也各不相同。因此，我们构建一个有向加权网络来描述各种波动模式之间的关系。

当下，越来越多的汽车制造商和零部件制造商希望将工业服务外包，以获得专业高效的服务，提升设备运行的可靠性，提高企业的生产能力和运营效率，从而将更多的精力集中到市场调研、产品研发、产品质量提升以及生产工艺研究等核心业务上。

将每一个字串视为网络的一个顶点，符号序列中相邻的两个字串之间存在一条边，由前一个字串指向后一个字串。如果两个顶点和之间存在多条边，则边数即为这两个顶点之间边的权重w。

3 径流网络的性质

分别以金沙江屏山站1943年1月1号至1992年12月31号日径流时间序列与美国佐治亚州Ocumlgee河Macon站1958年1月1号至2007年12月31号日径流时间序列作为研究对象。金沙江屏山站径流序列来源于长江水利委员会水文局，共有18263个数据；Ocumlgee河Macon站径流序列来源于美国地质调查局网站 http://water.usgs.gov/ waterwatch/，含18250个数据。

3.1 聚类系数

对于有向加权网络，当考虑边的权重的时候，网络的某个顶点的聚类系数定义为[14]

图 1 给出了网络顶点的聚类系数与度值的关系。从图1中可以看出，两个网络顶点的聚类系数随度值的变化都较大，这意味着三个网络并不是完全随机的，而是在某种程度上具有类似于社会关系网络中“物以类聚，人以群分”的特性[15]。Ocumlgee 河日径流波动网络度值较小的顶点聚类系数较大，度值较大的聚类系数较小，不同于小世界网络的性质。聚类系数的这种性质说明网络的群聚特性既可能会发生在小的集团中，也可能会发生在大的集团中。对于随时间变化的径流来说，意味着群发性有时会反映在小的时间尺度上，有时又会反映在大的时间尺度上，即径流变化有多年的周期波动，又有年度的涨落，还有月的变化特征。而金沙江日径流波动网络聚类系数与度值的关系则正好相反，表明群发性更多的发生在大的集团中，径流变化的长期周期波动更明显。

图1 日径流波动网络顶点的聚类系数与度值的关系

3.2 平均路径长度

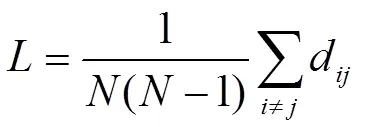
其中为顶点总数，d为顶点和的距离。表1给出了两个网络的平均聚类系数和平均路径长度。

表1 网络的平均聚类系数与平均路径长度

由表1可知，两条河流的日径流波动网络均具有较大的平均聚类系数和较小的平均路径长度。平均路径长度表征了由一种波动模式转变为另一种波动模式所花的时间，网络的平均路径长度均小于 2，表明模式的转换时间大约为6天左右，表现出短程相关性，这对于径流的短期预测具有一定的参考价值。较大的平均聚类系数表明各种波动模式存在小规模的群簇，群簇内部顶点之间的关联较好。如不同的季节内可能是不同的波动模式占主要地位，这些波动模式就构成一个群簇，不同的影响因素对应不同的群簇。Ocumlgee 河流日径流波动网络的平均聚类系数较大，平均路径长度较小，表明它的群簇性明显，模式转换较频繁。

3.3 中介中心性

在一个网络中，不同的顶点一般具有不同的重要性。顶点的拓扑重要性等价于该顶点与其他顶点的连接性，这种拓扑重要性可以用中介中心性来刻画[17, 18]。

信息在网络中的流通和传递往往要通过少数关键顶点才能以最短路径到达网络中的其他顶点，失去这些关键顶点将对网络的整体性质造成较大的影响。在复杂网络理论中, 用中心性来衡量一个顶点在网络中影响能力的大小，即获得、控制信息的能力。中介中心性反映了顶点在网络中的中介性和枢纽程度[19]。

网络中一个顶点的中介中心性测度g定义如下：设(,)为顶点对(,)之间所有最短路径的总数，路径的长度就是路径通过的各条边的权重之和。在这些路径中通过中间顶点的路径数记为c(,)，记

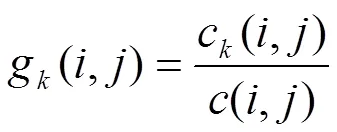
则顶点的中介中心性测度g为所有顶点对的g(,)之和，即

我们计算了两个网络各顶点的中介中心性测度，并对它们进行了排序，结果如表2、表3所示。从中可见，不同顶点的中介中心性测度有较大的差异。Ocumlgee河日径流波动网络前 30 个顶点对整个网络的中介中心性的贡献率达到了 85.03%，前10个顶点的g都在3%以上，中介中心性的贡献率达到41%。金沙江日径流波动网络前40个顶点对整个网络的中介中心性的贡献率达到了85.65%，前 7 个顶点的g都在3%以上，中介中心性的贡献率达到26%。这些贡献率较大的顶点的中介中心性等级与g%的双对数曲线图表明与g%呈幂律关系，如图2所示。这意味着某些顶点所代表的波动模式有着重要的意义，任意两个波动模式之间的转换经过这几个波动模式中转的概率较大，它们在一定程度上可以作为各种波动模式之间转换的前兆，对波动模式的转换具有重要的意义，对它们的研究将有助于更好地把握径流变化的规律。此外，在Ocumlgee河日径流波动网络中，、和三种波动模式的g% 均在5%以上，说明了该径流波动急剧增加和急剧降低模式的重要性，反映了该径流波动的剧烈化程度。

表2 Ocumlgee河Macon站日径流波动网络各顶点的中介中心性测度

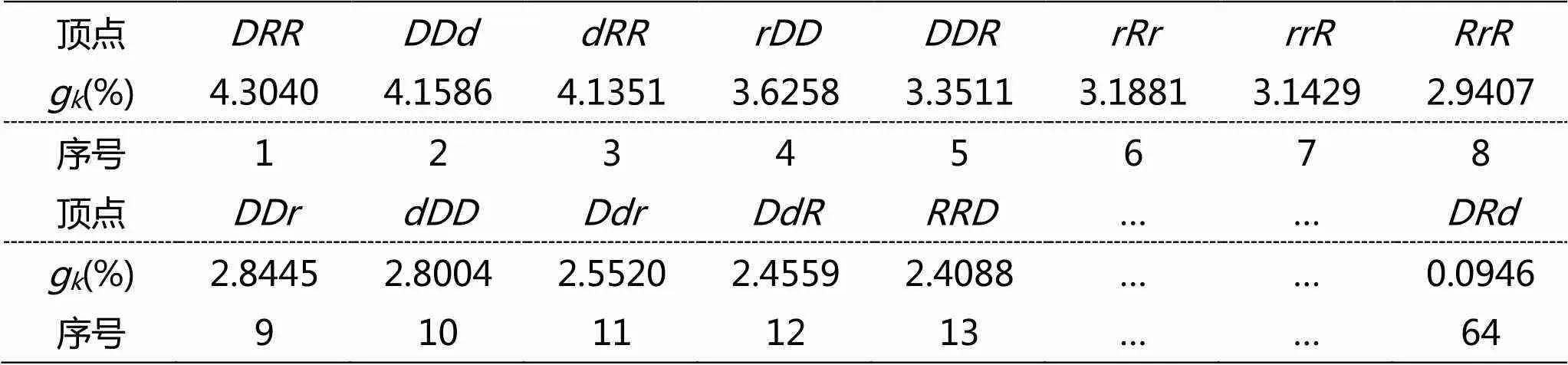
表3 金沙江屏山站日径流波动网络各顶点的中介中心性测度

图2 顶点的中介中心性等级与测度的关系。

4 结论

本文通过粗粒化方法将径流序列转化为符号序列，进而构建相应的复杂网络。通过对网络的聚类系数、平均路径长度和中介中心性测度等动力学统计特征量和拓扑参数的讨论发现，金沙江屏山站与Ocumlgee河Macon站日径流过程不是随机的过程，存在少数几种重要的波动模式。波动网络均具有较大的聚类系数和较小的平均路径长度，不同的波动模式之间存在着短程相关性，各种波动模式存在小规模的群簇，不同的群簇对应不同的影响因素，群簇内部顶点之间的关联较好，这对于径流的短期预测具有一定的参考价值。Ocumlgee 河流日径流波动网络顶点的度值和聚类系数呈负相关关系，说明径流变化有多年的周期波动，又有年度的涨落，还有月的变化特征。Ocumlgee 河日径流波动网络中、和三种波动模式的中介中心性测度较大，说明了该径流波动急剧增加和急剧降低模式的重要性，反映了该径流剧烈波动较频繁。不同顶点的中介中心性测度具有明显的差异，这意味着某些顶点所代表的波动模式有着重要的意义，在一定程度上可以作为各种波动模式之间转换的前兆，对它们的研究将有助于更好地把握径流变化的规律。

[1] 王文均，叶敏，陈显维. 长江径流时间序列混浊特性的定量分析[J]. 水科学进展，1994，5(2)：87-93.

[2] 侯玉，吴伯贤，邓国权．分形理论用于洪水分期的初步探讨[J]．水科学进展，1999，10(2): 140-143．

[3] Wang W, Vrijling J K, Gelder V, et al. Testing for nonlinearity of streamflow processes at different timescales[J]. Journal of Hydrology, 2006, 322: 247-268.

[4] Bof L H, Pruski F F, Da Silva L M, et al. Analysis of appropriate timescale for water diversion permits in Brazil[J]．Environmental Management, 2013, 51(2): 492-500 .

[5] 李新杰，胡铁松，郭旭宁，等. 0-1 测试方法的径流时间序列混沌特性应用[J]. 水科学进展，2012，32（6）：875-882.

[6] Khatibir, Sivakumarb, Ghorbanima, et al. Investigating chaos in river stage and discharge time series[J]．Journal of Hydrology，2012，414-415：108-117.

[7] Watts, D.J., S.H. Strogatz. Collective dynamics of small world networks [J]．Nature, 1998, 393: 440-442.

[8] Barabási, A.L., R. Albert. Emergence of scaling in random networks [J]．Science, 1999, 286(5439): 509-512.

[9] Qiang Tang，Jie Liu，Honglin Liu. Comparison of different daily streamflow series in US and CHINA, under a viewpoint of complex networks[J]．Modern Physics Letters B, 2010, 24(14): 1541-1547.

[10]郝柏林．复杂性的刻画与“复杂性科学”[J]．科学，1999，51(3): 3-8．

[11]Wackerbauer, R., A. Witt, H. Atmanspacher, et al. A comparative classification of complexity measures [J]．Chaos, Solitons & Fractals, 1994, 4(1): 133-173.

[12]张佃中，谭小红，王智，等．基于等概率粗粒化的复杂度算法及其应用[J]．系统仿真学报，2008，20(15): 4096-4098．

[13]周磊，龚志强，支蓉，等．利用复杂网络研究中国温度序列的拓扑性质[J]．物理学报，2008，57(11): 7380-7389．

[14]陈卫东，徐华，郭琦．国际石油价格复杂网络的动力学拓扑性质[J]．物理学报，2010，59(7): 4514-4523．

[15]汪小帆，李翔，陈关荣．复杂网络理论及其应用[M]．北京：清华大学出版社，2006．

[16]何大韧，刘宗华，汪秉宏．复杂系统与复杂网络[M]．北京：高等教育出版社，2009．

[17]Freeman, L.C.. Centrality in social networks conceptual clarification [J]．Social Networks, 1978, 1(3): 215-239.

[18]Li P., B.H. Wang. Extracting hidden fluctuation patterns of Hang Seng stock index from network topologies [J]．Physica A, 2007, 378(2): 519-526.

[19]Goh, K.I., E. Oh, B. Kahng, et al.Betweenness centrality correlation in social networks [J]．Physical Review E, 2003, 67: 017101.

Dynamic Analysis on the Topological Properties of the Complex Network of Runoff Time Series

TANG Qiang1, HU Tie-song2

(1. School of Mathematics & Computer Science, Wuhan Textile University, Wuhan Hubei 430200, China; 2.State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan Hubei 430072, China.)

Based on the complex networks theory, daily runoff series of the Jinsha River in China and the Ocumlgee River in America are used for exploring the fluctuation characteristic of this runoff.A runoff time series can be transformed into a discrete symbolic sequence by preprocessing coarse graining, and a complex network will be created. Then some dynamic statistical features and topology parameters of two fluctuation networks, such as clustering coefficient, mean path length and betweenness centrality, are discussed. We find that the clustering coefficients of two networks are larger and mean path lengths are smaller, which indicates the short-range correlation exists in different fluctuation patterns. The betweenness centrality of different nodes have obvious difference, which means that some fluctuation patterns have important significance and can be as a conversion precursor between the various fluctuation patterns to some extent. These results contribute to understanding the variation of runoff process and have reference value for short-term prediction of runoff process.

Runoff Time Series; Fluctuation; Complex Networks; Coarse Graining; Clustering Coefficient; Mean Path Length; Betweenness Centrality

唐强（1974-），男，副教授，研究方向：时间序列非线性性质.

P333

A

2095－414X(2014)03－0087－05