环F2＋vF2上线性码的对称重量计数器

许和乾， 杜 炜， 王菊香

（1．合肥师范学院 数学与统计学院，合肥 230601；2．淮南师范学院 数学与计算科学系，淮南 232001；

3．安徽建筑大学 数理系，合肥 230022）

1 引 言

自上世纪八十年代以来，纠错码的发展更着重于如何把纠错码有效地应用到实际中去，解决实际使用中的很多有关问题，其中最重要的是与译码问题密切相关的码的最小距离、重量分布、覆盖半径和球半径等．在精确计算差错控制系统的译码错误概率和不可检错误概率时，知道码的重量分布是必需的．但确定码的重量分布是一个比计算码的实际最小距离还要困难的任务．正是由于这些原因，使得对码的最小距离、重量分布等问题的研究，在编码理论中一直是一个非常重要的研究课题．

重量计数器是研究码的重量分布的一种有力工具，利用MacWilliams恒等式可以很容易的从一个码的重量计数器得到其对偶码的重量计数器，这大大简化了某些码的重量分布的研究过程．在文献［1］中，MacWilliams首次给出了域Fq上线性码Hamming重量的MacWilliams恒等式．文献［2］则对环Z4上线性码的各种重量分布进行了系统的阐述，而文献［3－5］则研究了其它一些不同环上的Macwilliams恒等式．

对环F2＋vF2（v2＝v）的研究有很多［6－9］，施敏加等在文献［10－12］中定义了该环上的一种Gray映射，研究了该环上线性码及其对偶码的结构和相关性质以及相应的Macwilliams恒等式．本文在此基础之上，利用离散的Hadamard变换，建立了环F2＋vF2上线性码及其对偶码之间关于对称重量计数器MacWilliams恒等式，该重量计数器在实际当中便于应用，而该环上线性码及其对偶码之间关于Hamming重量和Lee重量的MacWilliams恒等式则可作为上述结果的进一步推论．

2 基本概念

为方便起见，记环F2＋vF2为R，R中含有4个元素:0，1，v，1＋v，其中v2＝v．这个环可以看做域F2上2维向量空间，环R有且仅有两个极大理想｛0，v｝和｛0，1＋v｝，因而R是局部环．环R的特征为2，v和1＋v是它的两个零因子．环R上的线性码C是指Rn的加法子模．对任意的x＝（x1，x2，…，xn），y＝（y1，y2，…，yn）∈Rn，定义x与y的内积为〈x，y〉＝x1y1＋x2y2＋…＋xnyn．设C是环R上长为n的线性码，C的对偶码定义为C⊥＝｛x∈Rn｜〈x，y〉＝0，∀y∈C｝，容易证明C⊥也是环R上长为n的线性码．

设C1，C2均为环R上长为n的线性码，如果码C1通过一个坐标置换，必要时将码元v与1＋v互换，能得到码C2，则称C1，C2为环R上等价的线性码．环R上任意一个非零线性码C都等价于一个由生成矩阵

所生成的线性码，而对偶码C⊥的生成矩阵为

更多关于环F2＋vF2的结果，建议参看文献［8－12］中相关内容．

3 环R上线性码的对称重量计数器

为了便于在实际中的使用，下面将在环R中建立一种对称重量计数器．

在R中，记D0＝｛0｝，D1＝｛v，1＋v｝，D2＝｛1｝．

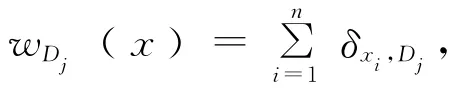
定义1:码C的对称重量计数器定义为:

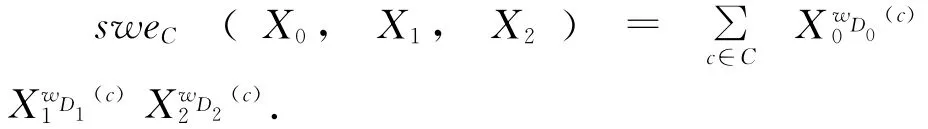
我们容易得到:

命题1:设C1，C2是R上两个长为n的线性码，若C1和C2等价，则它们的对称重量计数器相同．

定义映射Φ为:对∀a＋bv∈R，有Φ（a＋bv）＝（－1）b．

易得如下引理1:

引理1:对∀x＝（x1，x2，…，xn），y＝（y1，y2，…，yn）∈Rn，有

Φ（〈x，y〉）＝Φ（x1y1）Φ（x2y2）…Φ（xnyn）．

引理2:设C是R上长为n的线性码，C⊥为C的对偶码，则

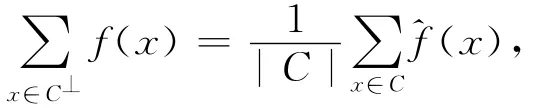
证明:仿照文献［5］中的证明易得本引理，此处从略．

定理1:设C是R上长为n的线性码，C⊥为C的对偶码，则

由引理1，

Φ（〈x，y〉）＝Φ（x1y1）Φ（x2y2）…Φ（xnyn），又对∀Di，

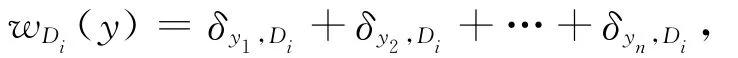
所以

其中s∈D1．

由引理2可知，

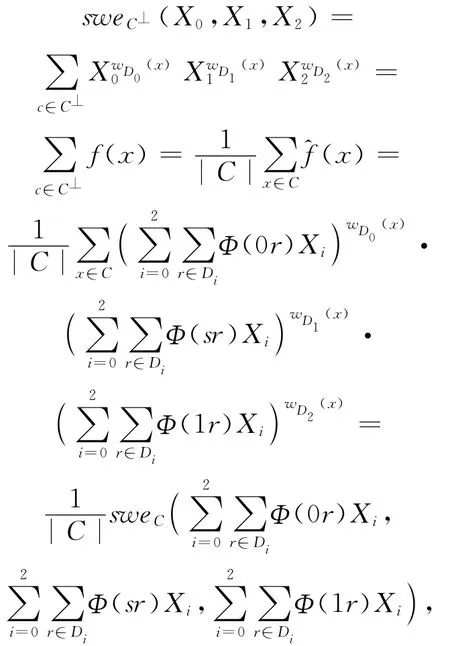
经计算，

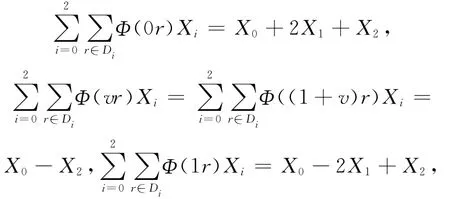
定理得证．

4 环R上线性码的对称重量计数器与Hamming重量计数器、Lee重量计数器间的关系

设C是R上长为n的线性码，对∀x＝（x1，x2，…，xn）∈R，x的 Hamming重量定义为

引理3［11］:（1）HamC（X，Y）＝sweC（X，Y，Y）；

（2）LeeC（X，Y）＝sweC（X2，XY，Y2）．

证明:在sweC（X0，X1，X2）中，令X0＝X，X1＝X2＝Y，易得结论（1）；令X0＝X2，X1＝XY，X2＝Y2，则易得结论（2）．

推论1:设C是R上长为n的线性码，C⊥为C的对偶码，则

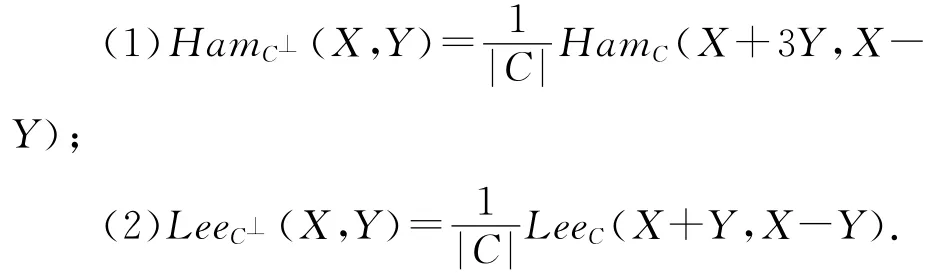
证明:根据引理3和定理1，易得本推论．

下面通过一个例子来说明本文结果的主要应用．

例:设C＝｛（0，0），（v，v）｝为环F2＋vF2上长为2的线性码，其对称重量计数器为

根据定理1，易得C⊥的对称重量计数器

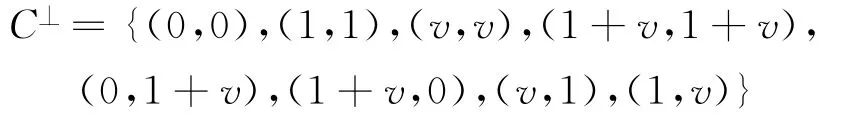
由对称重量计数器的定义得

二者结果一致．

1 MacWilliams F J．A theorem on the distribution of weights in a systematic code［J］．Bell System Technical Journal，1963，42（1）:79－84．

2 WAN Z X．Quaternary Codes［M］．Series on Applied Mathematics，Vol 8．Singapore:World Scientific Pub Co，1997．

3 朱士信．Zk－线性码的对称形式的MacWilliams恒等式［J］．电子学报，2003，25（7）:901－906．

4 余海峰，朱士信．环F2＋uF2上线性码及其对偶码的MacWilliams恒等式［J］．中国科学技术大学学报，2006，36（2）:1285－1288．

5 李雨，陈鲁生．环Fp＋uFp上线性码的 MacWilliams恒等式［J］．南开大学学报:自然科学版，2010，43（2）:78－84．

6 Bachoc C．Application of coding theory to the construction of modular lattices［J］．Journal of Combinatorial Theory Series A，1997，78:92－119．

7 Dougherty S T，Shiromoto K．Maximum distance codes over rings order 4［J］．IEEE Transactions on Information Theory，2001，47（1）:400－404．

8 Betsumiya K，Harada M．Optimal self－dual codes overF2×F2with Hamming weight［J］．IEEE Transactions on Information Theory，2004，50（2）:356－358．

9 Dougherty S T，Gaborit P，Harada M，et a1．TypeⅣself－dual codes over rings［J］．IEEE Transactions on Information Theory，1999，45（7）:2345－2360．

10 施敏加，朱士信，吴波．新四元环上线性码的研究［J］．合肥工业大学学报，2008，31（11）:1878－1881．

11 施敏加，朱士信，李平．环F2＋vF2上线性码的Mac－Williams恒等式［J］．计算机应用研究，2008，25（4）:1134－1135．

12 ZHU S X，WANG Y，SHI M J．Some result on cyclic code overF2＋vF2［J］．IEEE Transactions on Information Theory，2010，56（4）:1680－1684．