实腹式巨型框架与空腹式巨型框架抗震受力性能对比研究

熊裕林， 高荣誉

（安徽建筑大学 土木工程学院，安徽 合肥 230601）

0 引 言

随着建筑用地的日益紧张，高层、超高层建筑将是今后建筑领域研究的重点，而巨型结构作为高层建筑的重要结构形式将是研究的重中之重。空腹式巨型结构相对于实腹式巨型结构不但不会影响建筑的使用，反而因其在建筑材料上的更加节约，同等条件下具有更高的刚度和承载力，更好的延性和受力性能等诸多的优点，使得对空腹式巨型框架的受力性能的研究有其重要的理论价值和实际意义［1］。这一建筑结构体系在国内外的建筑领域也得到了较为广泛的应用，下面简单举一工程实例:

日本神户TC大厦 （见图1）是空腹式建筑结构体系的典型实例。该建筑是一栋地下3层，地上26层，平面尺寸为32m×33m，总高度达到103m的办公楼。该大楼采用的是钢结构巨型框架体系［1］，巨型柱由平面角部的竖向支撑与由方形钢管柱所围成的钢支撑筒共同组成，具体构件的相关尺寸大小见图所示。在该建筑的第15层和第26层（顶层），沿楼面四个角各设置一根巨型梁，由4榀桁架围成的高约4m、宽约6m的立体桁架组成的巨型梁与由4根巨型柱协同作用构成空间的单跨双层巨型框架。该巨型框架作为该大楼的主体结构，承担各楼层的重力荷载和由风、地震引起的全部水平荷载作用。

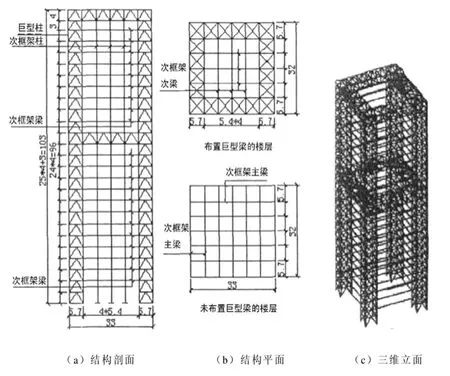
图1 日木神户TC大厦

1．1 时程分析基本理论［2］

时程分析法是对结构动力方程直接进行逐步积分求解的一种动力分析方法。采用时程分析法可以得到在地震作用下各个质点随时间变化的位移、速度和加速度，进而可以计算出构件内力和变形的时程变化。下面对本文所用方法简单介绍。

Hiber－Huges－Taytor（HHT）方法:1987年Hughes将Newmark－β法中的参数α进行修改，并将其导入结构动力方程并修改该方程，以后与Newmark－β方法无差别，这就是HHT法。导入后如下:

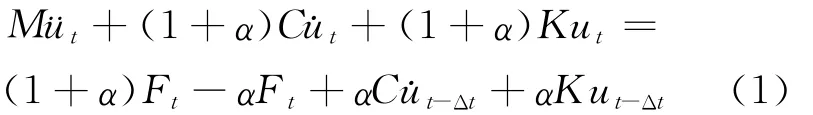
参数α在式中的取值范围为0～1／3。当α＝0，此法就是Newmark－β方法当其参数α＝0．5，β＝0．25的情况，也就是平均加速度法，并且各种方法中最高的精度可由α＝0解得，但过多的具有与时间步长同阶或低阶周期的高频振型振动会因此产生。高频振型可由选择负值的α被阻尼耗散的情况较严重，此情况发生过大。当选用时间步长越来越小时，阻尼它会减小，所以不为物理阻尼。通常结构为保证其收敛性，非线性分析中的α需要按负值来取得。

1．2 空腹式巨型框架

1．2．1 空腹式巨型框架的定义

空腹式巨型框架结构［3］是截面高度很大的主框架梁分解到相邻的两个界面上，使得这两层梁的截面高度都比较均匀，而且都不是特别高。同理，当主框架柱的截面高度很大时，也可将其一分为二。本文为分析简便，将只对实腹式主框架梁与空腹式主框架梁的受力性能进行比较。

1．2．2 空腹式巨型框架的等效截面高度计算

将b×h的钢筋混凝土实腹式矩形截面（图2），转化为b×he的钢筋混凝土空腹式矩形截面（图3），设每肢高度分别为αhe、βhe。

图2 实腹式截面

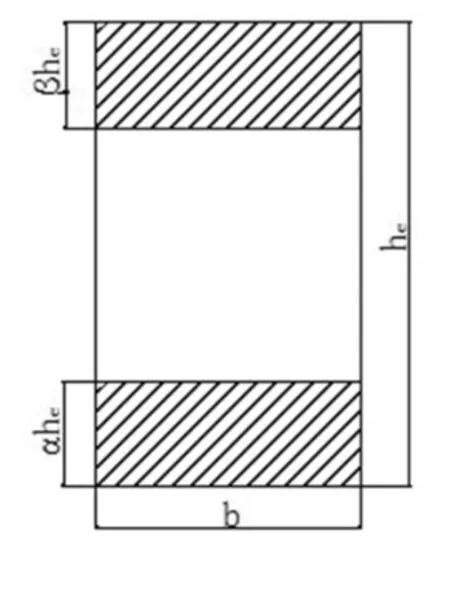
图3 空腹式截面

由材料力学知识可知，钢筋混凝土实腹式矩形截面的惯性矩为:

钢筋混凝土空腹式截面的形心坐标为:

钢筋混凝土空腹式截面的惯性矩为:

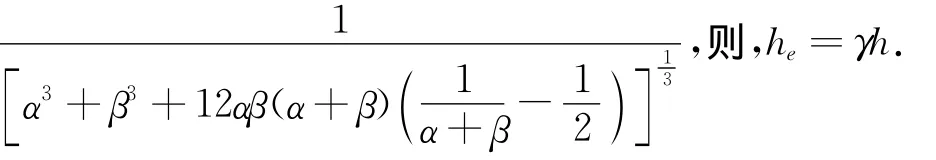
根据以上相关知识，本文中空腹式巨型框架取:α＝β＝0．4，γ＝1．003［4］，则he＝γh＝1．003×2．2＝2．2066m，αhe＝βhe＝0．4×2．2066＝0．88264m．

2 巨型框架结构动力时程分析

2．1 建立结构模型

为了研究实腹式主框架梁和空腹式主框架梁对巨型框架受力性能［4－5］的影响，现建立两个模型。模型均取24层，高度100．8m，实腹式巨型梁取1．1m×2．2m，巨型柱取2．2m×2．2m，混凝土强度等级C60，次框架柱取0．7m×0．7m，次框架梁为0．3m×0．7m，混凝土强度等级C40；对空腹式主框架梁空腹式巨型框架取α＝β＝0．4为例，he＝1．003×2．2＝2．2066m，梁上下肢高度为αhe＝βhe＝0．4×2．2066m＝0．88264m，实际施工中可取截面为1．1m×0．9m，其他与实腹式巨型框架一致。荷载取值按照《建筑结构荷载规范（GB 50009－2012）》中办公楼采用并稍加修改，具体设置荷载如下，楼面恒载2．0kN／m2，楼面活载341．7cm／s2，屋面恒载3．5kN／m2，屋面活载0．5kN／m2，为了考虑填充墙在地震下的作用，在所有楼面边梁上施加一个6KN／m均布线荷载。模型一和模型二都设置三根主框架梁，位置在第8层、第16层、第24层。如图4、图5所示。

图4 模型一空腹式巨型框架

图5 模型二实腹式巨型框架

设计使用年限50年，地震设防烈度为7度，设计其本地震加速度值为0．10g，Ⅱ类场地土，设计地震分组为第一组Tg＝0．35s，根据建筑设计抗震规范规定，采用时程分析法时所用地震加速度时程的最大值:多遇地震时为35cm／s2，罕遇地震时为220cm／s2［6］．钢筋混凝土实腹式巨型框架与空腹式巨型框架相关结构构件尺寸如下表（表1）所示。

表1 钢筋混凝土实腹式巨型框架与空腹式巨型框架相关结构构件尺寸

根据模态分析的结果，空腹式巨型框架与实腹式巨型框架前12阶自振周期见下表2所示。

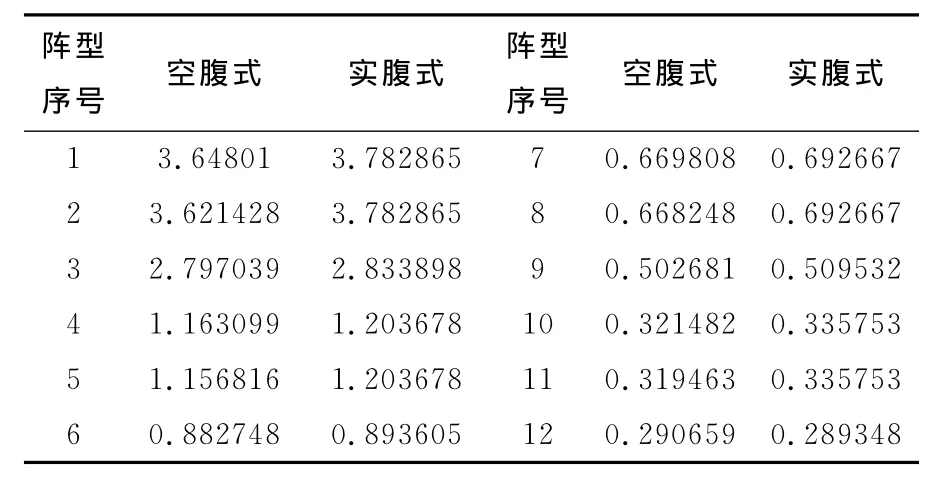
表2 不同算例的巨型框架结构的自振周期对比

由表2可知，对比空腹式巨型框架与实腹式巨型框架前12阶自振周期，由表1可知:实腹式巨型框架自振周期大于空腹式巨型框架自振周期；空腹式第一振型周期为3．65s，实腹式第一阶振兴周期为3．79s；较实腹式巨型框架而言空腹式巨型框架各阶振型的周期分布得更为密集［7］。

2．2 结构弹性动力时程分析

对模型一、二分别采用El－centro地震波，时程计算时间为30s，时间间隔为0．02s，其峰值加速度为341．7cm／s2；Taft地震波，时程计算时间为30s，时间间隔为0．02s，其峰值加速度为175．9cm／s2；Lanzhou地震波，时程计算时间为20s，时间间隔为0．02s，其峰值加速度为196．2cm／s2。经时程分析，为简便起见，这里只给出模型一、二结构在El－centro地震波作用下结构楼层侧移、层间位移角、顶层位移、基底剪力见图6、图7、图8、图9所示（图6纵轴表示楼层侧移，单位mm，横轴表示楼层层数；图7纵轴表示层间位移角，单位rad，横轴表示楼层层数；图8纵轴表示基底剪力，单位KN，横轴表示时间，单位s；图9纵轴表示顶层位移，单位mm横轴表示时间，单位s）。

图6 El－centro波下楼层侧移

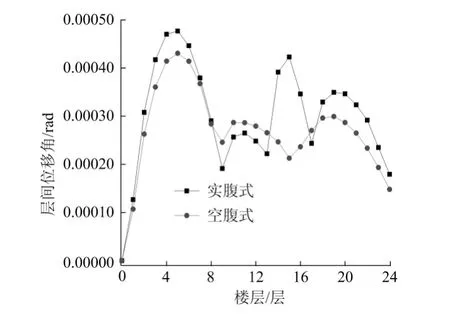
图7 El－centro波下层间位移角

图8 El－centro波下基底剪力

图9 El－centro波下顶层位移

3 结 论

经创建模型并进行相关分析可得出表3:

表3 钢筋混凝土实腹式巨型框架与空腹式巨型框架相关指标对比

由上表可得:

1、在 El－centro波、Taft波、Lanzhou波作用下实腹式巨型结构结构和空腹式巨型结构的最大层间位移角均小于规范要求的1／550的限值。以结构在El－centro波作用下为例，实腹式结构的最大楼层侧移为28．115mm，空腹式结构的最大楼层侧移值为31．744mm，实腹式相对空腹式相对减少了11．43%，但在其他几种波下，有不同的结论。

2、实腹式巨型结构的基底最大剪力达到1574．281kN，空腹式巨型结构的基底最大剪力达到1815．208kN，实腹式相对减少13．27%，但在其他几种波下，有不同的结论。

3、实腹式截面积为2．42m2，空腹式截面积为1．98m2，节约建筑材料约20%，且更便于施工。

对比空腹式结构而言，在地震波作用下，实腹式结构可以吸收更多的地震能量，从而使得实腹式巨型框架结构的各性能曲线变化要比空腹式巨型框架结构的平缓、柔和，楼层侧移有显著减小，且越到结构的顶部楼层侧移减小的越明显。简言之，在多遇地震作用下，空腹梁巨型框架抗震受力性能并不比实腹梁优越。

1 张红霞．钢筋混凝土巨型框架结构抗震设计研究［D］．重庆:重庆大学．2004．5

2 高荣誉，汤薛．巨型框架主框架梁均匀布置动力时程分析 ［J］．安徽建筑工业学院学报，2012，20（1）:1－3．

3 沈蒲生，孟焕陵，刘杨，等．钢筋混凝上空腹巨型框架结构体系研究［J］．建筑结构，2006，36（5）:5－13．

4 沈蒲生．巨型框架结构设计与施工［M］．北京:机械工业出版社，2007:15－22．

5 林倩．巨型框筒结构的动力特性研究［D］．南宁:广西大学土木工程学院，2005．

6 GB50011——2010，建筑抗震设计规范［S］．北京:中国建筑工业出版社．

7 严平，叶献国．钢筋混凝土巨型框架结构弹塑性地震反应分析的研究［D］．合肥工业大学．2010．4．