高速列车铝型材外地板结构振动与隔声量分析

张媛媛，沈火明，肖新标，李翔宇

(西南交通大学力学与工程学院，成都 610031)

列车轻量化技术是发展高速列车的关键技术之一。近年来，铝合金挤压型材的发展及其具有的一系列优点使铝合金成为高速列车车体的主导材料。高速列车铝型板材为带筋薄板，在质量轻的同时又减少了很多横向构件，从而使车体质量大幅降低。高速列车在运行中的振动和噪声问题目前尤为突出，为此国内外众多学者一直在探究高速列车车体结构的振动及声辐射问题。文献［1］基于混合有限元-统计能量法及周期子结构原理，建立了高速列车波纹外地板声学特性仿真模型，分析了波纹板结构及波纹板加夹板结构等在不同腹板倾角下的隔声性能。文献［2］测量了高速铁路动车组列车在不同距离、高度处的噪声，分析了其时间、频谱及空间分布特性。文献［3］探索了一个新方法来估计和测量铁路车辆的传输损耗，其中包括数值分析法结合按比例缩小的混响室的测量。文献［4］利用材料声学测试系统对敷设不同厚度黏弹性阻尼层的板进行声学分析。在国内，混合有限元-统计能量法也被广泛地应用在航空等行业。文献［5-6］在混合法的基础上引入周期子结构以提高计算效率。文献［7-10］提出了有限元与统计能量分析的混合方法，用于解决中频问题。本文采用统计能量分析原理，研究了高速列车铝型板材的固有特性及其隔声性能。

1 矩形薄板弯曲振动的有限元理论

对板经过单元离散后，可以获得薄板振动的有限元方程

式(1)中:M、C、K和F分别为系统质量矩阵、阻尼矩阵、刚度矩阵和载荷向量。当C=0，F=0时，得到结构的无阻尼自由振动方程

设式(2)解的形式为X= ψejωt，解得

由线性代数知识得

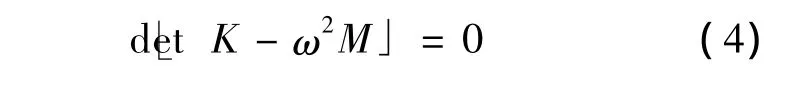
根ω2称为特征值，是结构固有频率的平方。

2 统计能量法基本理论

2.1 子系统的确定

统计能量法能把复杂的机械系统或声学系统划分为不同的模态群，并从统计意义上把大系统分解成若干个便于分析的独立子系统。统计分析能量模型必须能清楚地表示振动能量的输入、储存、损耗和传输的特性。

2.2 模态密度

由板的横向强迫振动方程式可得其模态密度为

式(5)中:Ap为平板表面积;R为平板截面的回转半径;Cl为纵波速。该式可计算任何形状、任何边界条件下的二维平板密度，且通过观察可知其模态密度与频率没有关系。

由三维波束空间得声场的模态密度为

式(6)中:As为声场的总表面积;ll为总的棱边长度;Ca为声速;V0为网格体积;ω为圆频率。

2.3 隔声量

在所研究结构的上、下两侧定义2个声腔，给上声腔一个激励，下声腔仅接受由上声腔通过结构传来的声激励，则结构隔声量的计算公式如下

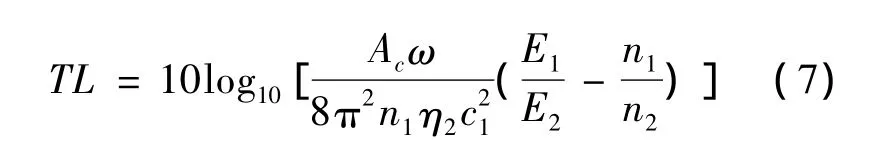
式(7)中:E1、E2和 n1、n2分别为上、下声空腔的能量和模态密度;Ac为结构与声空腔耦合面积;C1为声速;ω为带宽的中心频率;η2为下声空腔损耗因子。

3 实例计算分析

某高速列车铝型材外地板为中空带筋薄板，弹性模量E=0.71×1010Pa，泊松比ν=0.33，密度ρ=2 700 kg/m3。上地板厚3 mm，下地板厚4 mm，筋板厚2.5 mm，地板高h=80 mm，地板分析模型如图1所示。

图1 地板分析模型

3.1 铝型材外地板固有特性计算

为分析地板固有频率及模态分布特点，选取的板材尺寸长l=1.2 m，宽d=1.4 m，采用自由边界条件。固有频率如表1所示，图2～7为振型图。

由表1可知结构的前6阶固有频率为0。这是因为计算时对板材采用了全自由边界条件，结构首先进行刚体运动，计算结果与实际相符合。由模态图可知:带筋板材在小于第11阶固有频率时，上、下板连同筋板作为一个整体在振动，可等效为均质薄板结构;直到第12阶时只有上板发生振动，下板及筋板几乎未发生变形。因此，可以认为带筋薄板存在一个截止频率，当低于该截止频率时，铝型材外地板可等效为均质薄板;当高于该频率时，筋板将整个板材分成若干小区域，局部模态变形将不可忽略。

表1 d=1.4 m、l=1.2 m时板的固有频率 Hz

图2 第7阶模态

图3 第8阶模态

图4 第9阶模态

图5 第10阶模态

图6 第11阶模态

3.2 板材尺寸对固有频率及截止频率的影响

当板宽d=1.4 m固定时，分别计算了板长l为2、3、4 m时的固有频率。如表2～4所示，表5列出了它们的截止频率。

图7 第12阶模态

分析可知:板长的变化只影响其低阶频率，前6阶均为刚体位移，且板尺寸越大，越容易进入模态变形;随着阶数的增高，板尺寸对固有频率的影响也随之减小，其分布也越加密集。由表6可知:板尺寸的变化对其截止频率几乎没有影响。

表2 d=1.4 m，l=2 m时板的固有频率 Hz

表3 d=1.4 m，l=3 m时板的固有频率 Hz

表4 d=1.4 m、l=4 m时板的固有频率 Hz

表5 板在不同长度下的截止频率 Hz

3.3 隔声量的计算

研究对象为文献［11］中的铝型材地板，已知其截止频率为400 Hz，图8、9分别为等效板的材料参数和计算模型。图10为铝型材地板在不同阻尼因子下的隔声量。在图10中:第1条曲线为文献［11］等效板的阻尼系数谱，采用1/3倍频程。计算结果与文献完全吻合，说明模型设置正确合理。下面用验证过的模型计算结构阻尼系数分别为0.1%、0.25%、0.5%、1%、2%、2.5%、3%时的隔声量。分析可知:结构阻尼对噪声的传播有明显的抑制作用，且阻尼越大，结构的隔声效果越好。

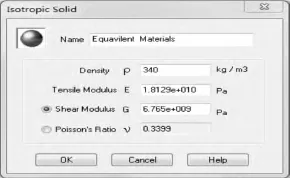
图8 等效板的材料参数

图9 计算模型

图10 板在不同阻尼因子下的隔声量

4 结束语

本文采用统计能量分析原理并利用VA One软件，计算分析了高速列车铝型材外地板的固有特性，研究了板材尺寸对截止频率的影响及结构阻尼因子对隔声量的作用。计算结果表明:板材尺寸仅影响其低阶频率，对高频区几乎没有影响;板材长度对截止频率的影响并不显著;结构阻尼对噪声的传播有明显的抑制作用，且阻尼因子越大，结构的隔声效果越好。

［1］沈火明，张玉梅，肖新标.高速列车波纹外地板低噪声优化设计［J］.交通运输工程学报，2011，11(2):65-71.

［2］愈悟周，王晨，毛东兴.高速铁路动车组列车的噪声特性［J］.环境污染与防治，2009，31(1):74-71.

［3］Tae Min Kim，Jeung Tae Kim.Comparison Study of Sound Transmission Loss in High Speed Train［J］.The Korean Society for Railway，2011，4(1)19-27.

［4］符俊杰，韩宝坤，鲍怀谦.敷设粘弹性阻尼的板的振动与声辐射分析［J］.声学技术，2009，28(6):142-144.

［5］陈书明，王登峰，曹晓琳，等.车内噪声FE-SEA混合建模及分析方法［J］.振动工程学报，2010，23(2):140-144.

［6］邹元杰，张瑾，韩增尧.基于FE-SEA方法的卫星部组件随机振动条件研究［J］.航天器环境工程，2010，27(4):456-461.

［7］LANGLEY R S，BREM NER P.A hybrid method forth evibration analysis of complex structural acoustic systems［J］.Journal of the Acoustical Society of America，1999，105(3):1657-1671.

［8］LANGLEY RS.The response of two dimensional periodics tructures to point harmonic forcing［J］.Journal of Sound and Vibration，1996，197(4):447-469.

［9］LANGLEY R S.The response of two dimensional periodics tructures to impulsive point loading［J］.Journal of Sound and Vibration，1997，201(2):235-253.

［10］LANGLEY R S，BARDELL N S.The response of two dimensional periodic structures to harm-onic point loading:atheoretical and experimentalstudy of a beam grillage［J］.Journal of Sound and Vibration，1997，207(4):521-535.

［11］Ying Guo.Systems definition and floor component analysis［C］//EUROPEAN COMMISSION DG RESEARCH.EUROPEAN.Ulf Orrenius:［s.n.］，2011:1-33.