基于粗糙集与关联规则的教师科研能力评价

李 梁，张建刚

(重庆理工大学计算机科学与工程学院，重庆 400054)

随着社会和科学技术的快速发展，高校的科研能力日益成为高校整体综合实力的一种标志。教师是学校科研工作的主力军［1］，但由于科研活动指标众多，且相互交叉影响，如何准确判断指标与教师科研能力的潜在关系已成为当前高校面临的一个重要问题。普通的统计分析已不能满足对教师科研能力评价的需求且普遍存在时间滞后、工作繁多等缺陷，而且评价过程中的人为主观因素往往成为影响评价正确性的不确定性因素［1］。

近年来，很多学者使用关联规则对高校科研能力或者教师科研能力进行挖掘分析。在教师科研评价指标繁多的情况下，没有对科研众多指标进行约简，而是直接使用关联规则算法进行挖掘分析，在属性维数尚未约简的情况下使用关联规则算法，这在形成候选项集、频繁项集和产生规则等步骤时大大增加了时间复杂度和空间复杂度。

针对上述问题，本文在参考国内外相关研究成果的基础上引入粗糙集理论中邻域粗糙集的相关性质，采用基于邻域粗糙集属性约简的贪心算法对教师科研能力指标进行约简，在不影响产生规则的前提下，求得影响教师科研指标的关键核属性，减少指标空间维数，然后结合关联规则Apriori算法挖掘教师科研能力与关键指标之间的潜在关联。

1 教师科研能力评价指标体系构建

通过研究相关文献［2-3］，结合高校教师的实际科研活动情况，笔者将科研活动大体上分为科研论文、科研项目、著作、获奖以及专利等一级指标，并根据一级指标划分不同等级的二级指标。如科研项目根据项目级别可划分为国家级项目、省部级项目、厅局级项目、横向和校级项目。其中校级项目为满足学校内部需求而开发的项目，在绩效计算评分过程中所占的分数比较低，故在评价教师科研能力评价指标体系中将其略去。综上所述，教师科研能力评价指标体系可用图1所示的层次结构指标体系描述。

图1 教师科研能力评价指标体系

2 基于邻域粗糙集的属性约简贪心算法

2.1 教师科研数据的连续性特征

本文的教师科研数据采用重庆市某高校对参与科研活动的教师按照评分规则进行积分计算得到，所得的科研绩效积分为同一量纲，教师科研数据是连续的指标数据，因此科研数据具有连续性特征。

2.2 约简算法的选择

经典粗糙集理论［4-6］定义在等价关系之上，对数值型数据的处理首先需要进行离散化处理。但是由于教师科研数据具有连续的特征，数据离散化后可能会丢失某些重要的信息，而且不同的离散化策略可能会影响评价模型的输出结果［7］。本文不再使用必须对数据进行离散化的经典粗糙集理论，而是引入了邻域粗糙集理论对教师科研进行优化和属性约简［8］。

2.3 属性选择贪心算法

属性选择过程常采取前向贪心搜索策略，通过测试加入新的候选属性后度量指标的变化，生成新的属性子集。以粗糙集属性依赖度作为度量指标时，需计算属性子集下的正域样本个数［9］。以往在逐个向已选条件属性集E中添加任一新属性r时，需要重新依次判断各个样本是否在正域内。根据其性质，若样本x为E上的正域样本，则x也是(E+r)上的正域样本，即新加入的属性仅对区分边界样本有效。根据这一特性，在计算决策属性D对(E+r)的属性依赖度时，只需判断原来负域中的样本即可，由此可能大大减少样本判断次数。

若U中样本个数为D，在已选属性子集E下，正域样本集为S，D对E的属性依赖度为k，加入属性r后，U-S中的样本在(E+r)下正域样本为s，个数为n，则D对(E+r)的属性依赖度为(k+n)/N。

在判断某个样本是否在正域时，由于需要计算邻域，所以其他样本无论是否已判定在正域内都将被用到。

3 关联规则算法

关联规则是描述一个事务中事件之间同时出现的规律的知识模式，是数据库中存在的一类重要的、可被发现的知识。关联分析的目的是找出数据库中隐藏的关联网，挖掘出隐藏在数据库中的一些关联规则，这些规则体现属性(数值)频繁地在特定数据集中出现的条件，通常表现为“同时发生”或“从一个对象可以推断出另一个对象”。利用这些关联规则可以根据已知情况对未来未知问题进行推测判断。

设 I={i1，i2，…im，}是项集，其中 ik(k=1，2，…，m)可以是购物篮中的物品，也可以是保险公司的顾客。设任务相关的数据D是事务集，其中每个事务T是项集，使得T⊆I。设A是一个项集，且A⊆T。

关联规则是如下形式的逻辑蕴涵:A⇒B，A⊂I，B⊂I，且A∩B=∅。关联规则有如下两个重要的属性:

支持度:P(A∪B)，即A和B这两个项集在事务集D中同时出现的概率。

置信度:P(B|A)，即在出现项集A的事务集D中项集B也同时出现的概率。

同时满足最小支持度阈值和最小置信度阈值的规则称为强规则。给定一个事务集D，挖掘关联规则问题就是产生支持度和可信度分别大于用户给定的最小支持度和最小可信度的关联规则，也就是产生强规则的问题。

最经典的关联规则算法是R.Agrawal，Imielinski和 Swam等人提出的 Apriori算法。支持度(support)和可信度(confidence)是描述关联规则的两个重要概念，前者(support)用于衡量关联规则在整个数据集中的统计重要性，后者(confidence)用于衡量关联规则的可信程度。

Apriori算法使用一种称作逐层搜索的迭代方法，k项集用于搜索(K+1)项集。首先，算法通过扫描数据库累积每个项的计数，并收集满足最小支持度的项，找出频繁1项集的集合，该集合记做L1;然后L1用于找到频繁2项集L2，L2用于找到L3，如此下去，直到不能再找到频繁K项集。找每一个Lk均需要进行一次数据库全扫描［9］。

为了提高Apriori的效率，算法引入连接步和剪枝步满足Apriori的性质:频繁项集的所有非空子集也必须是频繁的。

连接步:为找Lk，通过将Lk-1与自身连接产生候选K项集的集合Ck。

剪枝步:Ck是Lk的超集，所有的频繁K项集都包含在Ck中。扫描数据库，确定Ck中每个候选项的计数，如果候选K项集的(K-1)项子集不在Lk-1中，则该候选也不可能是频繁的，可以从Ck中删除。

4 教师科研指标数据的处理

4.1 指标数据获取和处理

教师科研能力指标体系主要采用图1所述的指标属性。由于依据某高校科研活动评分规则得到的教师科研活动得分实际上是连续型数据，所以数据之间存在着量纲和数量级的不同。本文选择邻域粗糙集属性约简贪心算法对科研指标进行属性处理，所以首先对所得的决策表初始数据进行归一化处理，然后采用贪心算法对归一化后的数据进行属性的重要性比较，得到约简后的属性，从而构造新的事务数据表作为关联规则算法的输入数据。教师科研能力指标数据如表1所示。

表1中属性科研活动数据来自重庆某高校2009—2011三年来部分教师的科研数据，它以某高校制定的科研工作绩效计分方法为依据，根据科研活动的级别以及等次进行分数计算，并且依据参与科研活动成员数量及角色分工的不同，按照成员参与重要度顺序、进而按照不同的比例进行得分计算。表1中的教师科研能力作为决策属性用G表示，其中:4表示科研能力很强;3表示科研能力较强;2表示科研能力一般;1表示科研能力较差。

表1 教师科研能力指标体系数据集

4.2 基于邻域粗糙集指标属性的约简

对表1中指标数据使用极差归一化变换，指标数据值都在(0，1)，变换公式为

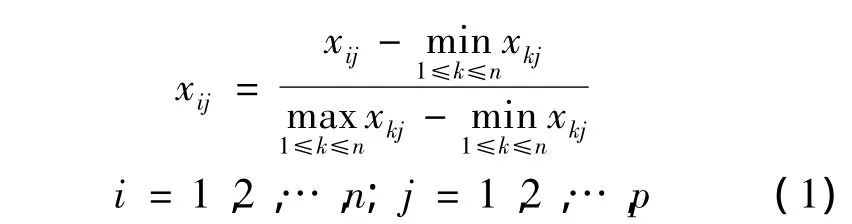
对表1进行指标数据连同决策属性与科研指标数据归一化之后，使用属性约简的贪心算法［11］进行属性之间重要性比较，通过设置不同的邻域半径得到的属性重要程度不同。程序选择基于哈尔滨工业大学胡清华副教授对粗糙集的研究，设置重要度下限为0.000 1，若求得某一属性的重要度小于0.000 1，则视其为很不重要的一列属性，将其作为冗余属性。在反复比较邻域半径不同值情况下，以高校普遍教师科研活动事实为依据，最终选择邻域半径为r=0.27，求的决策表中约简属性为［X1，X3，X4，X5，X6，X8］，即将国家级项目、厅局级项目、横向项目、核心期刊论文、三大检索论文以及公开发表的论文组成新的决策表作为关联规则事务数据，如表2所示。

表2 属性约简快速算法相关参数及约简结果

从约简后的核属性可知，大多高校教师的科研活动都集中在科研项目和科研论文方面，对于其他的科研活动比如专利、著作等重视程度较差。而对于科研项目，则众多的是横向项目，重要度为0.666 7，国家级项目重要度为0.190 5，说明教师更多地参与国家级项目不仅有助于提高自身科研素质，还可以提高学校参与国家级项目的比例。

4.3 指标数据的离散化处理

关联规则Apriori算法只能处理字符型变量和结果变量，故对于归一化之后的指标数据要根据数据变换规则进行离散化处理，并用不同的字符代表不同的指标数据范围。不同的指标数据在归一化之后保持相同的性质，对其进行离散化，离散化标准为0～0.15;0.16～0.30;0.31～0.45;0.45～0.6;0.61～1。其中，对于教师科研能力等级 G 划分为L4、L3、L2、L1，依次表示科研能力很强、较强、一般、较差。离散化后的数据如表3所示。

表3 教师科研能力离散化数据

4.4 关联规则Apriori算法对离散数据的挖掘

输入挖掘需要的参数，使用关联规则的Apriori算法进行挖掘，如最小值支持度计数Support=19%，最小置信度Confidence=50%。使用关联规则在于挖掘教师科研活动中国家级项目、厅局级项目、横向项目与核心期刊论文、三大检索论文、公开发表论文之间的内在关系，故前向数为2，后项数为1即为教师的科研能力等级，得到的规则如表4所示。

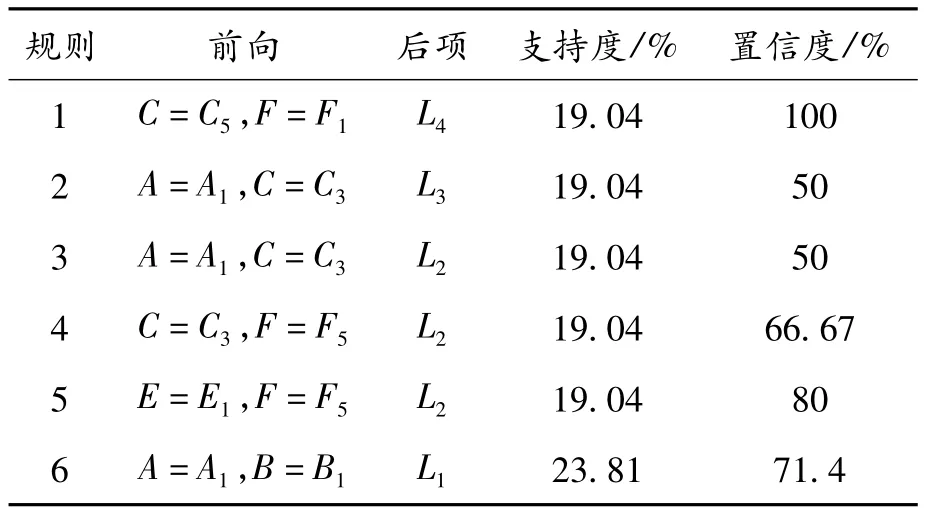
表4 教师科研能力提出的规则

4.5 规则分析

由规则1可知，教师科研能力很强，在科研项目尤其是横向项目上表现比较优秀，虽然在科研论文方面表现稍有不足，但是科研项目的比例弥补了教师在论文方面的不足;由规则2和规则3可知，当教师在国家级项目表现较差，横向项目表现良好时，教师的科研能力较强或者一般，支持度均为19.04%，其置信度均为50%;由规则4可知，教师在横向项目表现良好，且公开发表论文表现较差时，其科研能力为一般;规则5则显示教师核心期刊论文较差但是公开发表的论文很强的情况下，其科研能力为一般，公开发表的论文弥补了核心论文方面的缺陷;由规则6则可得在满足最小支持度下，教师在国家级项目和厅局级项目均表现较差时，其科研能力较差。

综上可得，影响教师科研能力的主要因素是国家级项目和核心期刊，以及三大检索论文的发表情况。对于科研能力很强的教师，其科研项目和科研论文往往不能同时达到优秀。如规则1所示，教师在横向项目达到优秀，但是在论文公开发表方面却仅为及格，因此学校决策层应采取一定措施，指导教师将参与的项目结合其论文发表，则教师科研水平将会更上一个层次。规则2、3表示科研项目表现一般情况下，教师科研能力为较强和一般的置信度均为50%，这类型的教师在论文方面的成就直接影响其科研能力，故决策层应根据实际情况加强教师的科研论文。对科研能力较差的教师，学校应给予更多的机会让他们参与项目的进度以及专业知识的学习，提高其专业知识水平，进而提高学校的科研活动能力。

5 结束语

本文率先引入邻域粗糙集理论与关联规则算法的结合，利用其属性约简快速选择算法对众多教师科研能力指标进行重要度约简，以某高校3年来科研数据为依据，求得影响教师科研能力的关键属性;对约简后的数据用关联规则的Apriori算法进行挖掘分析，不仅减少了算法生成规则的时间、空间复杂度，而且不影响规则的挖掘分析，最终求得教师科研能力与科研活动之间的深层关联，为学校决策层在科研活动方面提供事实依据。经验证，粗糙集与关联规则的结合在教师科研能力评价方面有一定的实用性，有助于高校合理分析教师的科研能力内在关系，为决策分析提供了事实依据，并为准确地对教师的科研能力进行评价衡量，从而全面了解教师信息提供一个有力的工具。

［1］徐守军，高波，等.数据挖掘技术在科研管理中应用前景初探［J］.中华医学科研管理杂志，2005(4):214-216.

［2］张剑平.高校教师科研能力评价指标体系设计研究［J］.黑龙江高教研究，2006(5):101-103.

［3］王京文，胡忠望，肖建华，等.高校教师科研水平评估指标体系的研究［J］.湖南工程学院学报:社会科学版，2006，16(2):73-75.

［4］常犁云，王国胤，吴渝.一种基于Rough Set理论的属性约简及规则提取方法［J］.软件学报，1999，10(11):1207-1211.

［5］石云，孙玉芳，左春.基于Rough Set的空间数据分类方法［J］.软件学报.2000，11(5):673-678.

［6］Suguna N，Thanushkodi K G.An Independent Rough Set Approach Hybrid with Artificial Bee Colony Algorithm for Dimensionality Reduction［J］.American Journal of Applied Sciences，2011，8(3):261-266.

［7］杨明.一种基于改进差别矩阵的属性约简增量式更新算法［J］.计算机学报，2007，30(5):815-822.

［8］邓胜，戴小鹏，陈垦，等.粗糙集理论在农业生物灾害预测中的应用［J］.安徽农业科学，2006，16(2):73-75.

［9］Han Jiawei H，Kamber M.数据挖掘概念与技术［M］.范明，孟小峰，译.北京:机械工业出版社，2007.

［10］谢中华.MATLAB统计分析与应用:40个案例分析［M］.北京:北京航空航天大学出版社，2010.

［11］胡清华，于达仁，谢宗霞.基于邻域粒化和粗糙逼近的数值属性约简［J］.软件学报，2008，19(3):640-649.