横梁腹板开孔剪切稳定性加强方式
葛俊波,张世联,郑轶刊
(上海交通大学 船舶海洋与建筑工程学院,上海200240)
0 引 言
实际船舶中为了方便管线布置,常需在横梁腹板上开孔,这将影响横梁的强度和稳定性。目前,国内外学者对梁腹板开孔后的强度和稳定性都进行了一些研究,由于开孔腹板剪切稳定性难以用解析法计算,研究一般采用有限元法或试验法进行。对于梁腹板开孔后的剪切稳定性问题,文献[1-6]对梁腹板开孔形状、尺寸及位置等变化对腹板剪切稳定性的影响进行了研究。图1[6]对比了不同长宽比板格在腹板开孔前后的剪切稳定系数,表明腹板开孔将导致其剪切稳定性损失,同时也将降低整根横梁的极限承载能力[7-8],因此需要对开孔进行加强。目前国内外对腹板开孔剪切稳定性的加强方式研究较少,文献[6,9,10]进行了一些研究,但是仅限于研究正方形板格开孔,且开孔尺寸都不超出规范要求(开孔高度d/b≤0.5)的情况,对加强构件尺寸讨论不够全面。
本文针对腹板开孔影响其剪切稳定性问题,对横梁腹板开孔剪切稳定性加强方式进行探讨。文中以腹板开圆孔(开孔高度范围为d/b=0.35 ~0.75)的横梁为例,应用有限元弹性屈曲分析方法,探讨加强筋、围缘扁钢和复板3 种常用加强方式在不同加强尺寸下的加强效果。最后对横梁腹板开孔的加强设计提出一些合理的建议。

图1 四边受剪开孔板的稳定系数Fig.1 Buckling coefficients of perforated beam webs under shear loading
1 有限元弹性屈曲分析方法的基本理论
本文使用MSC.Nastran 软件对开孔板进行弹性屈曲分析。弹性屈曲分析的基本假定是:失稳前结构处于小变形状态,可以不考虑几何非线性对平衡方程和几何方程的影响,同时材料始终处于弹性状态。此时,结构总刚度矩阵K 可表示为

式中:KE为结构弹性刚度矩阵,是结构固有的属性,与载荷无关;KG(σ)为结构几何刚度矩阵,又称初应力刚度矩阵,表示结构在变形状态下的刚度变化,是应力σ 的线性函数[11]。
使用Nastran 对模型进行弹性屈曲分析前,需要给结构施加一个初始载荷p0,从而在结构内产生与之成比例的应力σ0。Nastran 的弹性屈曲分析过程如下:
1)对结构进行静力计算,得到KE和KG(σ0);
2)假定载荷增大使结构内应力达到失稳临界值σcr=λcrσ0,则结构几何刚度矩阵变为KG(σcr)=λcrKG(σ0),结构总刚度矩阵为K=KE+λcrKG(σ0);
3)弹性屈曲分析归结为求解线性特征值方程,即:

从中可解得一系列特征值λcr,i,及对应的位移模态φi。
一般关注最低阶特征值λcr,1,将其乘以初始载荷p0,即得结构的临界载荷pcr,1,对应的位移模态φ1即为屈曲模态。
2 开孔横梁腹板有限元模型、载荷、边界条件
对于一根腹板开孔横梁,可取一块包含开孔的腹板板格作为研究对象,建立有限元模型,腹板、加强材都以板单元建立。开孔附近单元大小一般不大于板格短边长的1/30[10]。细化网格到粗网格应平缓过渡。板格四周的剪切作用一般简化为单位均布应力[2-3,5,7,9]。翼板和相邻板格对该板格的约束作用一般可保守看做简支,并约束刚体位移。横梁腹板开孔参数、载荷和边界条件如图2所示。
文献[6,9-10]仅针对正方形板格进行了加强方式研究,事实上屈曲系数随长宽比a/b 增大而减小(见图1),当a/b≥4 时才趋于稳定,因此本文针对a/b=4 的腹板板格进行加强方式研究。
板格具体参数为:板长a=1 600 mm,半宽b=400 mm,板厚t=5 mm,开孔中心位置xc/a=1/2和yc/b=1/2。

图2 横梁腹板开孔参数、载荷和边界条件Fig.2 Hole parameters,loading and boundary conditions of beam webs plate

图3 典型的开孔横梁腹板板格有限元模型Fig.3 Typical finite element model of beam web plate panel
3 加强方式及加强构件尺寸
3.1 加强方式的布置形式和尺寸参数
文献[6,9-10]中提出了许多加强方式,本文仅研究目前常用的3 种加强方式:加强筋,围缘扁钢和复板,它们的布置形式和参数如图4所示。图中加强筋和围缘扁钢的作用主要是提高开孔附近腹板平面的抗弯刚度,复板的作用主要是增加开孔附近腹板抗剪切面积。
下面分别讨论3 种加强方式的尺寸变化对其剪切稳定性加强效果的影响,尺寸范围如下:

图4 开孔腹板板格加强方式Fig.4 Reinforcement of perforated beam web plate panel
1)加强筋:假定加强筋紧贴开孔边缘;厚度为定值ts=0.5 t,高度变化hs=(0.1 ~0.5)d;
2)围缘扁钢:厚度为定值tr=0.5 t,高度变化hr=(0.1 ~0.5)d;
3)加强复板:厚度变化tf=(0.2 ~1.1)t,宽度范围变化lf=(0.1 ~0.7)d。
加强效果用板格开孔加强后的临界剪切应力τcr与不开孔时的临界剪切应力τcr,0的比值来衡量。
3.2 加强筋加强方式
图5 给出了开孔孔径分别取d/b=0.35,0.5和0.75 时,τcr/τcr,0随hs/d 的变化曲线。从图中可看出:当hs/d >0.2 时,加强效果基本不变,说明加强筋抗弯刚度已经达到临界值,继续增大不能改变开孔板格的屈曲模态;加强筋对开孔孔径为d/b=0.75 的板格加强效果较差。图6 进一步给出了当hs/d=0.2 时,τcr/τcr,0随d/b 的变化曲线,从图中可知,当d/b >0.5时,加强筋加强效果随d/b 增大而迅速减小,这是因为开孔尺寸较大时,2 根加强筋之间的板格先失稳,形成了一个完整的屈曲半波,如图7所示。
3.3 围缘扁钢加强方式
图8 给出了开孔孔径分别取d/b=0.35,0.5和0.75 时,τcr/τcr,0随hr/d 的变化曲线。从图中可以看出,当hr/d >0.2 时,加强效果基本不变,说明围缘扁钢抗弯刚度已经达到临界值,使板格形成3 个屈曲半波,继续增大不能改变开孔板格的屈曲模态;围缘扁钢对不同开孔尺寸的板格都有较好的加强效果。
3.4 复板加强方式
3.4.1 加强复板厚度的影响

图5 τcr/τcr,0随hs/d 的变化曲线Fig.5 Variation of τcr/τcr,0 as a function of hs/d

图6 τcr/τcr,0随d/b 的变化曲线(hs/d=0.2)Fig.6 Variation of τcr/τcr,0 as a function of d/b
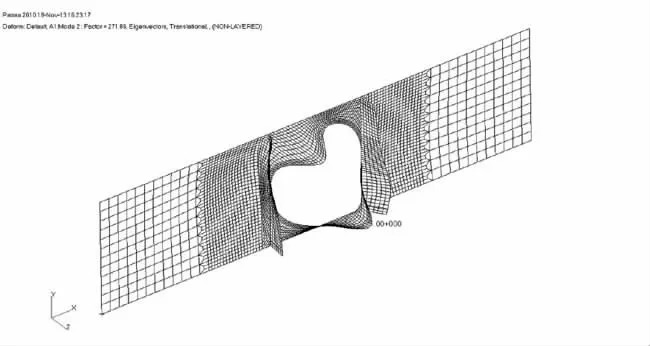
图7 d/b >0.5 时的板格屈曲模态图Fig.7 Buckling mode of plate panels with d/b >0.5
经计算,对应不同的复板宽度,加强效果随复板厚度的变化规律基本一致。图9 仅给出了开孔孔径分别取d/b=0.35,0.5和0.75,lf/d=0.4 时,τcr/τcr,0随tf/t 的变化曲线。从图中可看出,随tf/t增大,围缘扁钢加强效果明显提高;但是对各开孔尺寸的板格,tf/t 分别到达某一临界值后,加强效果提高速度都相对变缓,这是因为复板加强范围受限;取tf/t=0.65,即可使各开孔尺寸的板格临界剪切屈曲应力达到不开孔时的水平。

图8 τcr/τcr,0随hr/d 的变化曲线Fig.8 Variation of τcr/τcr,0 as a function of hr/d

图9 τcr/τcr,0随tf/t 的变化曲线(lf/d=0.4)Fig.9 Variation of τcr/τcr,0 as a function of tf/t
3.4.2 加强复板宽度的影响
图10 给出了开孔孔径分别取d/b=0.35、0.5和0.75,tf/t=0.65 时,τcr/τcr,0随lf/d 的变化曲线。从图中可看出,随lf/d 增大,围缘扁钢加强效果明显提高;取lf/d=0.3 即可使各开孔尺寸的板格临界剪切屈曲应力达到不开孔时的水平。
4 结 语
本文采用有限元弹性屈曲分析方法,针对长宽比为4、中央开圆孔的腹板板格,探讨了常用的加强筋、围缘扁钢和复板3 种加强方式在不同加强尺寸下对腹板开孔剪切稳定性的加强效果,得到以下结论:

图10 τcr/τcr,0随lf/d 的变化曲线(tf/t=0.65)Fig.10 Variation of τcr/τcr,0 as a function of lf/d
1)3 种加强方式基本都能使腹板开孔后的剪切稳定性提高到不开孔的水平;
2)当加强筋紧靠开孔边缘,高度hs大于0.2d时,继续增大对加强效果提升作用不大;
3)围缘扁钢高度hr大于0.2d 时,继续增大对加强效果提升作用不大;
4)复板加强方式的尺寸增大时,对腹板开孔剪切稳定性的加强效果不断提高,因此相比前两者更有效,但是材料消耗更多,如对开孔孔径d/b=0.5 的板格,将其临界剪切应力提高到不开孔的水平,复板加强所需的材料重量是加强筋的3 倍以上;
5)对于小开孔(d/b≤0.5)板格,要使其临界剪切应力提高到不开孔的水平,加强筋加强时,其尺寸建议取为ts=0.5t和hs=0.1d,围缘扁钢加强时其尺寸建议取为ts=0.5t和hs=0.2d,复板加强时,其尺寸建议取为tf=0.65t和lf=0.2d,其中加强筋所消耗的材料最少;对大开孔(d /b >0.5)板格,加强筋加强效果较差,建议采用围缘扁钢或复板加强,其尺寸分别取为ts=0.5t、hs=0.2d和tf=0.65t、lf=0.3 d。
以上分析结果和结论可对横梁腹板开孔的剪切稳定性加强设计提供一定的参考。
[1]NARAYANAN R,CHOW F Y.Experiments on perforated plates subjected to shear[J].The Journal of Strain Analysis for Engineering Design,1985,20(1):23-34.
[2]LEE M M K,KAMTEKAR A G.Elastic shear buckling of perforated webs in steel plate girders[J].The Structural Engineer,1989,67(22/21).
[3]李亚波.工字梁中心开椭圆孔腹板的屈曲性能研究[D].西安:西安建筑科技大学,2007.
LI Ya-bo.Study on buckling of web with oval openings in Ishaped beam[D].Xi′an:Xi′an University of Architecture and Technology,2007.
[4]CARLO P,EMANUELE M,CLAUDIO M.Linear and non- linear behavior of steel plates with circular and rectangular holes under shear loading[J].Thin-Walled Structures,2009,47:607-616.
[5]王勋.船体桁材开孔后的强度和稳定性研究[D].武汉:武汉理工大学,2009.
WANG Xun.Strength and buckling analyses of ship girders with cutout[D].Wuhan:Wuhan University of Technology,2009.
[6]徐秉汉,郭庆恒.船舶构件腹板开孔的弹性失稳与加强效果[J].中国造船,1987(3).
XU Bing-han,GUO Qing-heng.Elastic unstability and reinforcement of ship structural plate with cutout[J].Ship Building of China,1987(3).
[7]Steel beams with web openings[EB/OL].http://www.steel-insdag.org/teachingmaterial/chapter28.pdf.
[8]SHIN Dong-ku,CHO Eun-young,Kyungsik KIM.Ultimate flexural strengths of plate girders subjected to web local buckling[J].International Journal of Steel Structures,2013,13(2):291-303.
[9]查煜峰.开孔平板的剪切稳定性实验[J].实验力学,1989,4(4):406-410.
ZHA Yu-feng.Buckling of plates with hole subjected to in- plate shear[J].Journal of Experimental Mechanics,1989,4(4):406-410.
[10]CHENG Bin,LI Chun.Buckling behavior of strengthened perforated plates under shear loading[OL].Sciencepaper Online,2012,6.
[11]王勖成.有限单元法[M].北京:清华大学出版社,2003:649-651.
WANG Xu-cheng.Finite element method[M].Beijing:Tsinghua University Press,2003:649-651.

