多变异策略差分进化算法的研究与应用

吕铭晟,沈洪远,李志高,王 汐,龚 明,王俊年

(湖南科技大学信息与电气工程学院,湖南 湘潭 411201)

1 概述

差分进化(Differential Evolution,DE)算法[1]采用模拟生物进化的机制,通过种群内个体差异度生成差异个体,然后进行交叉、选择操作实现种群的进化。DE 算法适用性强,不依赖于问题辅助信息,容易实现,需要调整的参数少,非常适合于求解一些利用常规数学规划方法不能或难以求解的复杂优化问题。

许多文献对标准差分进化的不足提出了改进,如文献[2-3]分别将交叉概率和缩放因子设计为自适应,文献[4]提出采用动态更新种群的策略,文献[5]提出一种自适应差分进化算法(SDE)；文献[6]提出基于模糊控制的自适应差分进化算法(FADE)；文献[7]提出基于适应值的自适应差分进化算法；文献[8]提出自适应群体差分进化算法；文献[9]提出广义的变异策略方案,用户可以方便选择适合自己所求问题的变异操作类型；文献[10]提出基于邻域搜索的DE/target-to-best/1 算子；文献[11]提出多策略和控制参数自适应差分进化算法；文献[12]提出DE/rand/1/Either-or 算子。文献[13]提出双种群伪并行差分进化算法。迄今为止DE 已发展为一种在求解非线性、不可微、多峰值及高维复杂函数等类型问题的高性能强鲁棒的方法,已经在滤波器设计、聚类分析等领域取得了较好的应用[14-15]。

根据变异机制的不同,DE 有多种不同版本,其中,DE/rand/1 是标准差分进化所采用的变异策略,相对而言该变异策略操作简单,在低维单峰函数优化问题中具有收敛速度快、寻优精度高等优点。但在高维多峰复杂函数优化时,存在算法易早熟或后期收敛速度慢等不足。针对该问题,本文提出一种多变异策略差分进化算法(MDE)。通过引入改进的DE/best/1 变异策略对种群进行二次变异操作,以拓展算法搜索空间,使算法在交叉操作时能够有更大概率获取更多优秀的变异向量分量,进而从种群个体的“基因”上有效控制种群在进化过程中的多样性。为避免算法进化的盲目性,在其变异操作中都采用精英保留原则,并对其中部分优秀基因采用基因扩散处理。

2 标准差分进化算法的变异策略

与其他进化类算法类似,DE 算法首先初始化种群,然后对种群个体依次执行变异、交叉和选择操作,产生出子代种群,经过反复迭代最终得到所需的结果。

标准差分的变异策略如下：

(1) 第1 种变异策略DE/rand/1：

(2) 第2 种变异策略DE/best/1：

其中,r1,r2,r3∈[1,N]为随机选择的整数,且须满足：r1≠r2≠r3≠i；F为变异操作缩放因子,取值在(0,2)之间,控制变异向量的幅值。

3 多变异策略差分进化算法

3.1 变异策略

差分进化算法的核心操作为变异。对变异策略的选取决定了算法在进化过程中种群的走向,而贪婪的选择策略本身具有两面性,在低维单峰函数优化时能够保证算法始终向更小的方向进化,但在高维多峰复杂函数优化时,因为仅用贪婪选择策略,致使算法一旦搜索到某一较优秀局部最小时,算法在最优适应度上出现停滞,随着时间的累积,最终导致种群个体某些维变量陷入特定范围。根据式(1)和式(2)可知,如果所有个体某维变量过早趋于一致,在没有其他操作的干预下,种群丧失多样性,算法就会出现早熟。

为了增强贪婪算法的全局最优能力,使算法在处理多峰高维复杂函数问题优化时,避免算法在某一局部最小值时可能出现的停滞,避免个体种群多样性过早地丧失。本文采用2 种变异共存的方式优化经典差分算法。

改进变异策略DE/best/1：

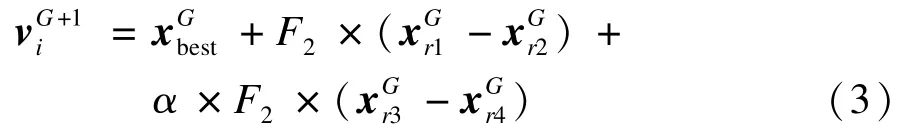
本文优化算法将2 种策略纵向结合,增加了种群的多样性,使算法的全局搜索能力得到有效增强。将DE/rand/1 作为变异策略1。将式(3)作为变异策略2,α为向量相关参数,α的加入使本次变异有了更多的选择空间；结合成多变异策略差分进化算法。变异策略2 的加入极大增强算法的搜索空间和在局部区域的搜索能力。MDE 算法较标准差分进化增加了多个控制参数和种群,使算法的搜索能力得到有效的加强且提供了更灵活的选择。

差分算法使用精英保留的原则。在此基础之上,本文研究采取了精英扩散和限制原则,使优秀的精英个体能影响其他个体的部分基因,而一些带有欺骗性的精英个体对其影响力进行限制。这也符合生物社会的规律,即优秀的个体对整个种群的进步应产生更大的影响力。反之,应减少。

在算法中加入扩散数值k,以决定精英的影响大小。本文算法中采取每一代进化,最优个体影响其他某一个体k维基因的方法。

采取精英扩散原则后,算法能在各阶段更有效地保留优势个体,更好地发挥了多变异策略的优势,提高了收敛速度。

3.2 算法流程

多变异策略差分进化算法的具体流程(图1)如下：

(1) 初始化种群,对参数进行设定。

(2) 计算种群个体适应度。

(3) 采用策略1 进行变异、交叉和选择操作。计算适应度,记录当前最优个体。更新整个种群的适应度。

(4) 采用策略2 进行变异、交叉和选择操作。计算适应度,记录当前最优个体。更新整个种群的适应度。将策略2 中最优个体的部分基因根据扩散数值k替代随机个体的对应基因。

(5) 判断步骤(4)得到的结果是否达到退出条件,若满足,结束,否则,跳转到步骤(2)继续执行。

图1 多变异策略差分进化算法流程

4 算法测试与结果分析

4.1 测试环境与结果

为验证MDE 的有效性,以常用的4 个Benchmark测试函数为例对MDE 进行测试,同时,与标准差分DE/rand/1 进行对比。算法最大函数评价次数为2.5e +05,各算法对于每个函数都独立连续运行20 次。

表1 中,CR1,CR2分别表示DE/rand/1、DE/best/1 2 种变异策略下算法的交叉概率；F1,F2分别表示缩放因子；α为相关系数；k为扩散系数。

表1 MDE 算法各控制参数设置

由表2 结果可知,当DE/rand/1 出现早熟现象时,DE/best/1 能够通过参数的调节防止算法早熟,可见其稳定性不如DE/rand/2。正是由于F2的存在弥补了DE/rand/1 稳定性的不足。而DE/rand/1 和DE/best/1 串行组合并非简单叠加,在结合两者优点的基础上,MDE 性能有了进一步的提高,使其整体性能在测试中表现最为优秀。

表2 20 次独立运行的最优解平均值

从算子的结构上进行分析,式xr1+F×(xr2-xr3)可分为2 个部分理解,xr1作为随机选择的基向量,F1×(xr2-xr3)可理解为以基向量为中心在其周围进行局部搜索。可见式(1)本身就兼有全局与局部搜索的特性,只是其全局搜索强于局部搜索。将式(2)改写为(xbest+F2× (xr2-xr3)) +α×F2×(xr4-xr5)),当α≠0 时,改进后的DE/best/1 相对于DE/best/1 而言多进行了一次变异,可以理解为改进后DE/best/1 其实是局部搜索能力得到加强的DE/best/1。并且DE/best/1 以当前最优个体为指引进行局部搜索,减少了其盲目性。同时,其随机性也扩展了算法的搜索空间,有利于增加种群的多样性。有效地提升了算法的整体性能。

4.2 参数设置

交叉概率CR虽不能对交叉操作提供精确的指导信息,但是通过对其数值大小的调节能够控制算法获取变异向量分量的能力,当CR较大时,在交叉操作中能以较大的概率从变异向量获取更多的分量,扩展算法的搜索空间；相反,则利于种群的多样性。CR2取值应该不小于CR1,原因是DE/best/1 策略较DE/rand/1 策略能产生更多的优秀变异向量分量,而这些分量需要较大的交叉概率获取。F2取值应少于F1,这是因为经过DE/rand/1 策略优化后问题的解已经向最优靠拢,而策略2 可以理解为是在前者的基础上微调,根据向量合成法则,F2和α×F2不宜较F1大。这有利于平衡算法的全局和局部搜索能力。当然还应该由具体问题的特性来设置F2和α,使算法的性能发挥出较好的优势,提高解决问题的效率。对于单峰函数的求解CR2取较大的值,有利于从DE/best/1 变异中获取更多优秀变异分量,使结果的精度越高。对于其他复杂的多峰函数,由于存在大量局部最小值欺骗,算法只能同时以较小的CR2逐步从DE/best/1 变异中获取优秀变异分量。

对缩放因子F的设置也必须考虑具体问题的特性,从数学表达式可以看出F2和α×F2是2 个可以互换的参数,因此,实验中3 个取值比较接近,也可以理解α×F2是在F2基础上的一种微调。因此,α的取值一般在1 附近。

扩散参数k的加入是为了使算法能在各阶段更有效地保留真正的优势个体及其潜在优势基因段,是对策略2 的很好补充,有效避免陷入早熟的问题。k的选取以种群个体维数M为度量,实验表明,k取(0.1～0.5)M,能对算法产生较好影响。

图2～图5 为4 个测试函数的仿真对比,本文将MDE 的实验结果和标准DE/rand/1 的结果以及将标准DE/rand/1 策略2 倍线性叠加的结果就行了比较。其中,DE 为标准差分；2XDE 为标准DE 线性叠加；MDE 为改进后的差分算法。

图2 Schwefel 2.22 函数适应度比较

图3 Schwefel 2.26 函数适应度比较

图4 Rosenbrock 函数适应度比较

图5 Sphere 函数适应度比较

5 电力负载分配问题

本文采用一个经典的38 个发电机的电力负载分配问题,发电机成本与发电量之间的关系如下：

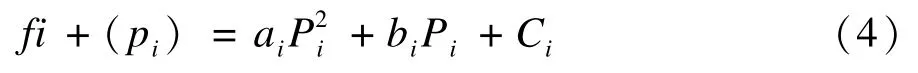
电机功率约束为：

电力平衡约束为：

当电力系统覆盖密集时可以忽略网络损耗,本文在计算中忽略了网络损耗,故电力平衡约束可简化为：

目标函数：

总负荷PD=6 000 mW。为了克服随机性影响,算例独立计算20 次。

表3 给出了算法的运算结果,以及与ISPO[16]算法的比较。本次测试中样本个数为50 个,迭代次数为10 00 次,F1=0.4,F2=0.4,α=0.75,CR1=0.3,CR2=0.3,k=5。由表3 可知,此算法取得了相对较好的结果。

表3 2 种算法的目标函数计算结果比较

MDE 算法的目标函数值最优曲线如图6 所示,由图可知,此方法求解经典电力负载分配问题快速有效。表4 为各发电机目标函数最优解。

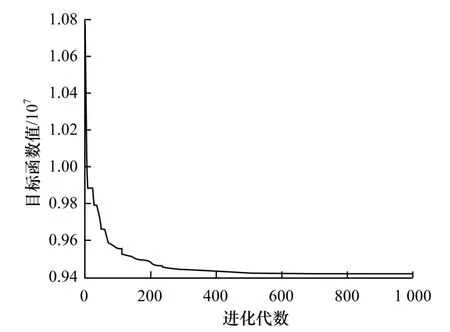
图6 MDE 算法的目标函数最优曲线

表4 各发电机MDE 算法的目标函数最优解

6 结束语

本文针对标准差分进化在高维多峰复杂函数优化中存在的不足,设计一种多变异策略差分进化算法。在4 个Benchmark 函数上与标准差分进化算法进行了对比,结果表明,改进算法在对算法的控制方面较标准差分进化算法更为灵活而且稳定,收敛速度和所得最优解精度方面都比标准差分进化算法有明显优势。通过电力负载分配模型求解结果表明,该算法是求解大规模电力系统经济负荷分配问题的有效方法。今后将在多变异的基础上,研究参数的自适应设置。

[1]Storn R,Price K.Differential Evolution——A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces[J].Journal of Global Optimization,1997,11(4)：341-359.

[2]许小健,黄小平,钱德玲.自适应加速差分进化算法[J].复杂系统与复杂性科学,2008,5(1)：87-92.

[3]邓泽喜,刘晓冀.差分进化算法的交叉概率因子递增策略研究[J].计算机工程与应用,2008,44(27)：33-36.

[4]肖术骏,朱学峰.一种改进的快速高效的差分进化算法[J].合肥工业大学学报：自然科学版,2009,32(11)：1700-1703.

[5]Salman A,Engelbrecht A P,Omran M G H.Empirical Analysis of Self-adaptive Differential Evolution[J].European Journal of Operational Research,2007,183(2)：785-804.

[6]Liu J,Lampinen J.A Fuzzy Adaptive Differential Evolution Algorithm[J].Soft Computing,2005,9 (6)：448-462.

[7]Ali M M,Törn A.Population Set-based Global Optimization Algorithms：Some Modifications and Numerical Studies[J].Computers &Operations Research,2004,31(10)：1703-1725.

[8]Teng N S,Teo J,Hijazi M H A.Self-adaptive Population Sizing for a Tune-free Differential Evolution[J].Soft Computing,2009,13(7)：709-724.

[9]Feoktistov V,Janaqi S.Generalization of the Strategies in Differential Evolution[C]//Proceedings of the 18th International Parallel and Distributed Processing Symposium.[S.l.]：IEEE Press,2004：165-170.

[10]Das S,Abraham A,Chakraborty U K,et al.Differential Evolution Using a Neighborhood-based Mutation Operator[J].IEEE Transactions on Evolutionary Computation,2009,13(3)：526-553.

[11]Pan Quanke,Suganthan P N,Wang Ling,et al.A Differential Evolution Algorithm with Self-adapting Strategy and Control Parameters[J].Computers &Operations Research,2011,38(1)：394-408.

[12]Price K,Storn R M,Lampinen J A.Differential Evolution：A Practical Approach to Global Optimization[M].[S.l.]：Springer,2006.

[13]吴亮红,王耀南,周少武,等.双种群伪并行差分进化算法的研究与应用[J].控制理论与应用,2007,24(3)：453-459.

[14]Paterlini S,Krink T.Differential Evolution and Particle Swarm Optimisation in Partitional Clustering[J].Computational Statistics &Data Analysis,2006,50(5)：1220-1247.

[15]Storn R.Designing Nonstandard Filters with Differential Evolution[J].Signal Processing Magazine,2005,22(1)：103-106.

[16]Chaturvedi K T,Pandit M,Srivastava L.Particle Swarm Optimization with Time Varying Acceleration Coefficients for Non-convex Economic Power Dispatch[J].International Journal of Electrical Power &Energy Systems,2009,31(6)：249-257.