道路网络中基于方向关系约束的CKNN 查询

孙海龙 ,王霓虹 ,王春艳

(东北林业大学a.信息与计算机工程学院；b.图书馆,哈尔滨 150040)

1 概述

随着无线通信技术的发展和具有GPS 定位功能的移动电话、PDA 等便携设备的普及,基于位置的服务(Location Based Service,LBS)得以快速发展,已广泛应用于地理信息系统、应急服务、汽车导航和旅游路径规划等领域[1]。空间查询与基于位置服务密切相关,其中,道路网络环境下移动对象的连续K 最近邻查询(Continouns K Nearest Neighbors,CKNN)是一类重要的查询请求,能够在道路网络环境下不断查找距离给定的查询对象最近的K个最近邻目标,例如,在消防指挥中,查找距离指挥中心最近的4 辆消防车。解决此问题的关键在于：(1)快速实时计算任意2 个移动对象之间的最短路径；(2)移动对象位置更新后查询结果的维护与管理。

国内外针对道路网络的CKNN 查询问题,学者们进行了深入研究。文献[2]提出IMA/GMA方法,处理查询对象和兴趣点对象在道路网上任意移动的CKNN 查询问题。该方法是处理基于道路网络的CKNN 查询经典算法,采用基于内存的数据结构存储网络边、结点以及查询信息,提出IMA/GMA 算法处理查询请求。IMA 算法从查询对象所在边开始扩展网络边,并遍历网络边上的兴趣点对象,形成初始KNN 查询结果集,同时以查询点为根,建立查询扩展树,处理查询请求、移动对象和道路边权重更新时的连续查询请求。GMA 采用IMA和共享执行机制,算法使用“序列”思想,即：序列上的查询请求结果为序列上的对象和序列端点处KNN 结果的并集,当多个查询请求处在同一序列上时可共享已获得的查询结果。为维护查询结果的更新,在计算初始KNN 时建立影响列表。IMA/GMA 算法适合于密集的道路网络。文献[3]提出MovNet 框架处理道路网络环境下的基于位置的查询,使用基于磁盘的R 树索引道路网络,基于内存的格网索引管理移动对象的位置更新,通过网格重叠计算算法将道路网与格网单元进行关联,完成基于位置的范围查询和KNN 查询。文献[4]针对IMA/GMA 算法中Dijkstra 算法进行网络距离计算时盲目扩展以及对象位置更新时盲目映像的缺点,提出ER-CKNN 算法,基于PMR-QuadTree 索引道路网络,基于格网索引移动对象位置,使用edgebitmap-encoding 技术结合A*启发式搜索算法,提高最短路径计算速度；同时,在查询时使用欧式距离约束限制K 近邻搜索区域；对象位置更新时,只对区域内的移动对象进行更新,从而加快查询处理速度。文献[5]针对基于道路网络的CKNN 查询处理,提出一种新的道路网络有向图模型,分别利用基于内存的哈希表和线性链表结构对移动对象当前位置和道路网络有向图模型进行存储和管理。通过引入单向网络距离度量和双向网络距离度量,提出单向网络扩展(UNE)算法和双向网络扩展(BNE)算法以支持不同语义的连续K 近邻查询处理,并采用影响树及网络扩展策略来减少连续K近邻查询更新的搜索代价。文献[6]针对数据频繁更新时查询性能下降问题,结合多核多线程技术,提出一种基于多线程的连续查询处理框架。该框架周期性重计算所有查询结果,将查询处理分为顺序执行的数据更新阶段和查询执行阶段,分别使用任务并行和数据并行的方法执行各阶段的操作。设计了数据更新阶段使用的数据结构,提出了查询处理阶段的K 近邻查询处理策略,包含离线预计算和在线K 近邻查询处理算法2 个部分,并对K近邻算法复杂性及多线程处理框架的加速比进行理论分析。以上文献采用了不同技术提高CKNN算法的执行速度,但是都没有考虑到方向关系约束条件在空间查询中的作用[7-8]。文献[8-9]研究了基于开放区域的方向关系查询技术以及三维环境下的方向关系建模,但没有考虑道路网络环境下的最近邻查询问题。

为提高CKNN 查询速度,本文将方向关系作为查询约束条件引入到算法中,提出基于方向关系约束的CKNN 查询CDR-CKNN 算法,处理道路网络环境下连续K 最近邻查询问题。

2 问题描述及相关定义

在基于位置的服务中,消防员、消防车辆等移动对象配备了具有定位功能的移动设备,移动终端周期性地将位置信息传送到服务器端。当用户提交CKNN 查询请求时,在服务器端基于道路网络距离完成查询请求,由于查询对象和兴趣点对象是不断运动的,实时获得连续KNN 查询结果是系统应用的关键。为提高KNN 查询速度,根据实际应用情况对已有算法进行改进：(1)预计算道路网络结点之间的最短路径；(2)由于移动对象的运动具有一定的方向性,因此将方向关系谓词作为空间查询约束条件引入CKNN 查询中,快速过滤掉与查询结果不相关的区域。

定义1(道路网络) 一个道路网可以建模为有向带权图G(N,E,W),其中,N表示道路边连接点和终点的集合；E(E∈N×N)表示道路网络边的集合,每条边e记作e(ni,nj),表示由起点ni和终点nj组成的结点序列构成,并且边不能存在环,即每条边是由n0,n1,…,nk系列结点组成的多段线,n0表示边的起点,nk表示边的终点,并且n0≠nk；W：E|➝R+表示边权值的集合,权值可以是道路边的长度、运行时间或者车流量等,如非特指,本文是指道路边的长度,图1 为部分道路网络及其对应的有向带权图。

从图1 可以看出,实际道路运行包括单行道和双向车道,在建模图形时用有向边表示。同时,查询对象和兴趣点对象(统称移动对象)在道路上运动时也具有方向性,下面对移动对象进行建模。

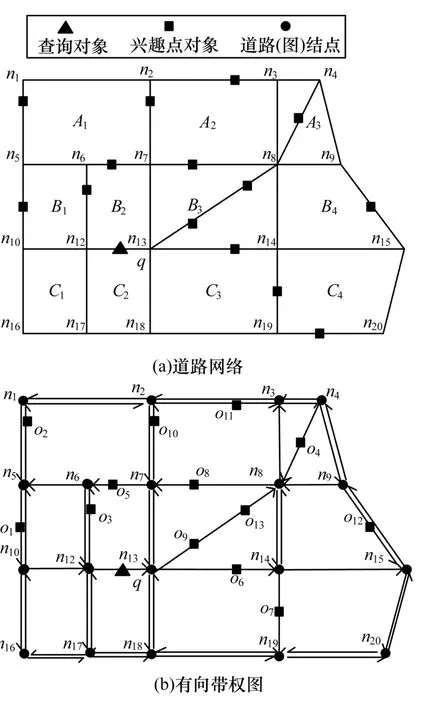
图1 道路网络及其对应有向带权图

定义2(移动对象) 在道路网络中,移动对象建模为：MO(oid,x,y,eid,pos,dir),其中,oid表示移动对象的编号；x,y表示移动对象的坐标位置；eid表示移动对象所在的道路边；pos表示移动对象在道路边上距离道路边起点的距离；dir表示移动对象运动方向,dir=1 表示从所在道路边起点向终点方向运行,dir=-1 表示从所在道路边终点向起点方向运行。移动对象可以是查询对象,也可以是待查询的兴趣点对象(Points of Interest,POI)。

定义3(道路结点的邻接链表) 为反映出道路网中U 型转弯和十字路口转向等交通规则,为道路网中的道路边结点设置一个单链表,表示通过该结点的道路边的转向关系。图2 为图1 所示道路网络中部分结点的邻接链表。对于道路边的交点n1,n5n5表示在结点n1处允许U 型转弯；n5n2表示移动对象在n5n2道路边上运动时,经过n1结点可以右转弯,其他结点含义相同。

图2 部分道路结点的邻接链表

定义4(道路边最短路径) 任意给定的2 条道路边：e1=(n1i,n1j),e2=(n2i,n2j),e1和e2之间的最短网络距离可以用2 条边起始点和终点之间最短路径的最小值表示,即：

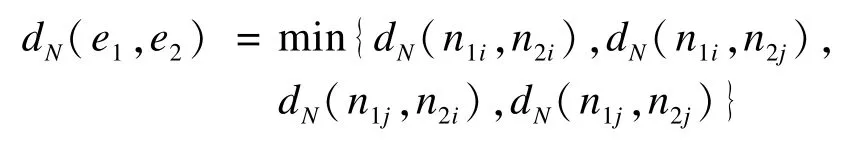
为提高系统的执行速度,预计算道路网络中各顶点的最短路径[10],在存储在数据库中,为计算道路网上任意2 个对象之间的最短路径做基础。

定义5(移动对象之间的最短路径) 在道路网络中,移动对象在道路边上的位置表示为：(e,pos),道路边e的权值记作：C(e)。假设2 个移动对象p1=(e1,pos1)、p2=(e2,pos2)分别在道路边e1和e2上运动,则移动对象p1 和p2 的最短网络距离表示为：

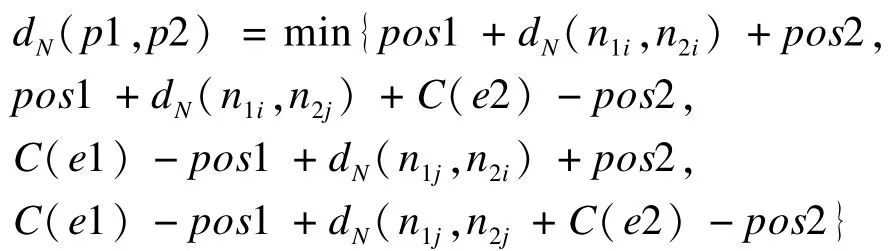
定义6(CKNN 查询) 参考对象和待查询的兴趣点对象都在道路网络边上自由运动,CKNN 查询是指每隔一定时间间隔查找距离查询对象q最近的K个对象。假设兴趣点对象集合S={p1,p2,…,pn},K 最近邻查询结果集为S′,S′⊆S,且|S′|≤K。对于任意数据对象p′∈S′,p∈S-S′,则有dN(p′,q)≤dN(p,q)。

3 索引结构设计

在道路网络环境中,能够有效存储和查找道路边上移动对象的最简单方法是将移动对象看作道路网的结点,利用定义1 对道路网建模,然后采用文献[11]提出的INE 方法进行查询。但是该方法存在一些缺陷：(1)将移动对象当作道路边结点对待,增加了网络的复杂度和Dijkstra 算法的运行时间；(2)移动对象位置经常变化,需要不断重建道路网结构。在实际应用中,道路网络结构往往是不变的,而移动对象不断更新位置,因此,道路网络和移动对象必须分别存储,本文提出一种3 层的索引结构,如图3所示。上层是一棵R 树,对道路网络进行索引,当查询点发出查询请求时,通过R 树可以快速定位查询对象所在的道路边；R 树的叶子结点指向道路边的实际存储,这两部分用来对道路网络中静态部分进行索引；第3 层hash 表部分以道路边的编号为hash 值建立hash 表,存储每条道路边上的移动对象标识,并通过移动对象标识连接到移动对象列表中。当移动对象进行位置更新时,首先在移动对象列表中完成信息的更新,然后更新道路边上的移动对象。静态道路网络部分不受影响。

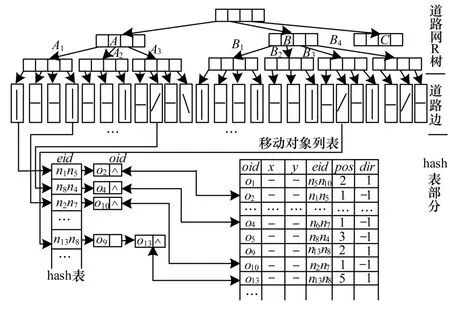
图3 道路网络及移动对象索引结构

4 CKNN 查询算法

在道路网络中,基于方向谓词约束的CKNN 查询分为2 个步骤：(1)基于方向关系完成KNN 查询请求；(2)更新KNN 查询结果。第(1)个步骤又可细分为过滤和精炼2 个步骤。

4.1 基于方向谓词约束的KNN 查询算法设计

移动对象运行在道路网中,当查询对象发出查询请求时,首先通过索引结构中的移动对象列表和hash 表的链接关系找到查询对象所在的道路边；然后将查询中的方向关系谓词通过构建开放图形转化为ArcGIS 中的Geometry 类；其次将Geometry 图形与道路网图层作相交运算,获得查询区域内的道路边,通过索引结构获得查询区域内的移动对象,获得候选结果集；最后利用预计算的道路网结点数据计算查询对象和候选结果集中各对象的最短路径,精炼出最终的KNN 查询结果。

定义7(锥形模型) 以参考对象为中心,将空间目标及周围区域划分成不同区域来表示对象之间方向关系的建模方法,适合于参考对象为点对象的建模情况。根据划分区域数量不同,通常分为四方向锥形模型和八方向锥形模型,如图4 所示。在四方向锥形模型中,用方向关系谓词集合：{E,S,W,N}表示空间对象之间的方向关系,分别对应东、南、西、北4 个方向；在八方向锥形模型中,用方向关系谓词集合{E,SE,S,SW,W,NW,N,NE}表示空间对象之间的方向关系,分别对应东、东南、南、西南、西、西北、北和东北8 个方向。从图4 可以看出,每个方向关系谓词都是一个由参考点和2 条边组成的开放区域,因此,可以用开放图形概念表示方向关系谓词。

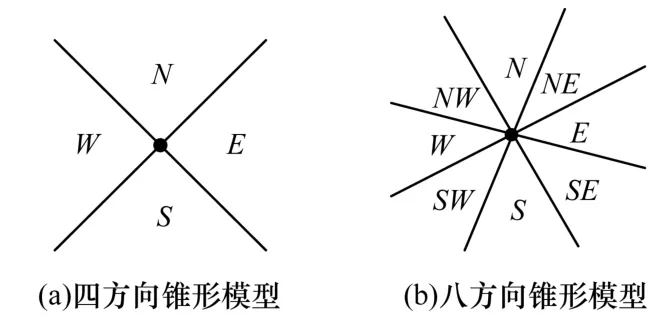
图4 锥形模型

定义8(改进的开放图形) 在文献[6]中提出开放图形概念,但是在实际道路网路查询中,查询范围是有一定距离限制的,改进的开放图形表示为：OpenShape(point,r,dir1,dir2),其中,point表示开放图形的顶点；r表示距离；dir1 表示起始端线的方向；dir2 表示终端线的方向,按逆时针方向,以弧度值计算。例如,在图4 中四方向锥形模型的东方向可表示为

算法1 给出了具有方向关系约束的道路网络KNN 查询过程,其中,KnnQuery代表查询算法的名称；q代表查询参考对象；dp代表方向关系谓词；K代表待查询最近邻对象的数量。

算法1KnnQuery(q,dp,K)

输入R-Tree

输出ResultList 满足查询条件的KNN 结果集

算法1 的时间复杂度计算主要集中在搜索R树、搜索hash 表、计算道路网与方向区域的相交运算和计算候选集中对象的最短路径等部分组成。在R树中搜索道路边的时间复杂度为O(NlogmN),其中,N为R 树中叶子结点总数,即道路边数量；m为每个结点最大分支数。hash 表通过hash 值进行搜索,时间复杂度为O(1)。道路网与方向区域的相交运算的时间复杂度取决于道路边的数量,时间复杂度为O(N)。候选集中各结点之间的最短路径计算采用Dijkstra 算法,时间复杂度为O(KlgK),K为候选集区域内道路网络结点数量；其他部分时间计算可忽略不计,因此算法1 的时间复杂度为：O(NlogmN) +O(KlgK) +O(N)。

算法1 中步骤2、步骤3 通过搜索道路网络的索引结构得到查询点q所在的道路边及其在道路边上的位置；步骤4～步骤6 用来查找查询区域内的道路边,步骤4 将查询条件中的方向关系谓词转换为开放图形,但是开放图形的开放区域没有边界限制,影响算法查询效率。步骤5、步骤6 引用ArcGIS Server 中图层的Intersect 相交运算帮助获得查询区域内的道路边,步骤5 采用定义8 提出的改进开放图形将开放区域转化为Geometry,然后与道路网图层进行Intersect运算,快速过滤掉与查询结果无关的道路边,获得查询区域内的道路边。步骤7～步骤15 计算查询区域内满足查询条件的所有候选兴趣点对象。步骤7～步骤9 通过查询索引结构中的hash 表获得查询区域内道路边上的所有移动对象,但是有些兴趣点对象并不在查询区域内,如图5(a)所示。当查询移动对象q以东方向5 km 以内的最近邻对象时,虽然边n7n8位于查询区域内,但兴趣点对象o8不在查询区域内。为解决该问题,步骤10～步骤14使用Geometry 的Contain包含运算,对候选兴趣点对象candidateMO 中的每个对象进行验证,从而得到查询区域内的KNN 候选兴趣点集。步骤16～步骤19 根据预计算的道路网络结点之间的最短路径,快速计算查询点q与候选兴趣点集candidateKNNs 中的各对象的最短路径,并统计对象个数k,同时按照距离升序排序,存入ResultList 中。步骤20～步骤25 根据候选最近邻对象个数决定查询是否继续。如图5(a)所示的左斜线填充的查询区域,如果查询2 个最近邻对象,则只需取出ResultList 中距离最近的前2 个对象即可。如果要查询4 个最近邻对象,则必须扩展查询区域,如图5(b)中右斜线填充部分为扩展区域,然后利用步骤7～步骤19 的方法计算扩展区域内的兴趣点对象,直到得到K个最近邻对象,将包含K个最近邻对象的查询区域保存在knnArea 中,供连续查询KNN 时使用,算法运行结束。

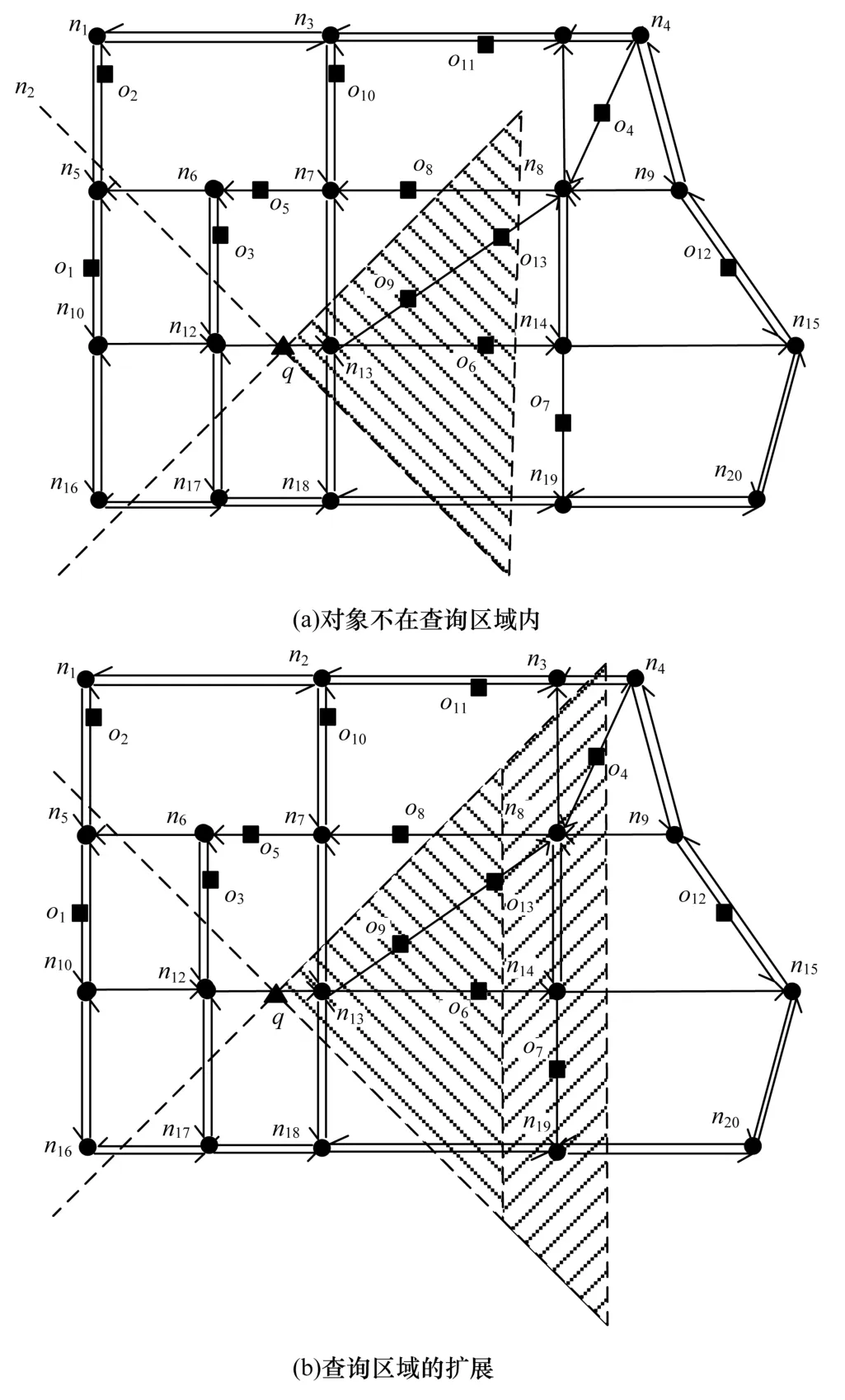
图5 KNN 查询算法实例

4.2 连续K 最近邻查询实现

当系统再次发出KNN 查询请求时,最简单的处理方法是采用4.1 节提出的算法重新计算KNN,但是受移动终端计算能力和通信速度的影响,计算速度难以满足要求。为了提高连续KNN 查询的执行速度,可以维护4.1 节算法的查询结果来提高连续KNN 查询的性能。移动对象(包括查询点对象和兴趣点对象)不断移动时,道路网络结构和道路边连接点的邻接关系并不变,只是对移动对象的位置和坐标进行更新,根据移动对象位置变化不同,可以分为2 种情况维护KNN 查询结果：(1)当查询对象q位置不变,兴趣点对象位置更新时,查询对象q的KNN 查询区域不变,可以利用算法1 得到的knnArea 区域加速更新算法；(2)查询对象q位置更新或者方向关系约束条件改变,必须重新计算KNN集合。算法2 给出了连续KNN 查询的算法实现。

算法2UpdateKnnQuery(q,dp,K)

输入R-Tree

输出ResultList 满足查询条件的KNN 结果集

算法2 中步骤3～步骤11 处理第(1)种情况时的查询结果更新情况。只有落入knnArea 区域内的兴趣点对象才影响查询结果。根据移动对象位置更新后落入knnArea 区域内兴趣点对象个数多少分为3 种不同情况。步骤5～步骤6 是恰好有K个对象落入查询区域内,这是最理想的情况,K个对象即为更新后的查询结果；步骤7～步骤8 表示落入knnArea 区域内对象数大于K,则利用算法1 中的步骤计算k′个对象与查询对象q之间的最短路径,并按照升序排序,将前K个对象作为查询结果；步骤9～步骤10 表示落入knnArea 区域内对象数小于K,则必须扩展查询区域半径,继续计算最近邻对象,直到达到K为止。步骤12～步骤13 处理第(2)种情况,由于查询对象q位置改变或者方向关系约束条件改变,原有的方向区域不再有效,不能利用knnArea 区域更新查询结果,必须利用算法1 对KNN 集重新计算,算法2 结束。

5 实验对比及分析

本文从兴趣点对象(POI)数量、查询请求数K、道路网规模以及不同方向关系模型等方面测试本文提出的CDR-CKNN 查询算法与IMA/GMA 算法的性能对比情况,实验测试数据集来自TIGER/Line 下载的加利福尼亚州洛杉矶市(Los Angeles,LA)道路网数据,LA 数据集中包含266 335 条双向边,195 010个道路结点,利用Brinkhoff[12]设计的基于道路网络的移动对象产生器生成兴趣点对象集。下载的shp 格式数据经过转换工具,生成node 结点数据和edge 道路边数据,作为移动对象产生器的输入因子,实验参数如表1 所示。实验系统采用Java 语言编写,运行环境为AMD 2.31 GHz 三核处理器,内存2 GB,Windows XP SP3 操作系统。每次测试只改变其中的一个参数值,其他参数采用默认值。

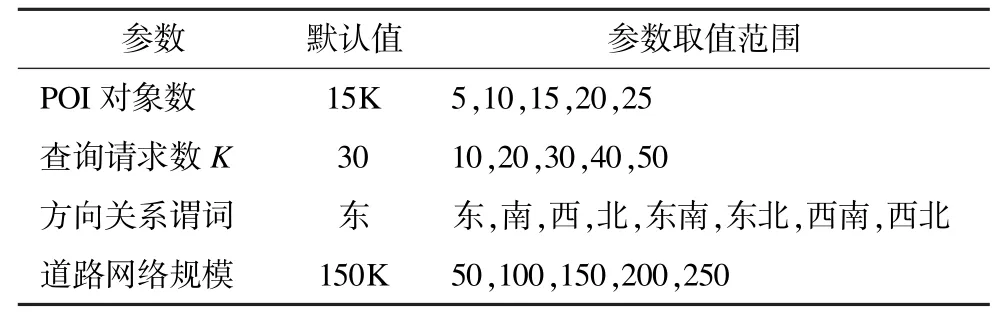
表1 实验参数

5.1 道路网络规模大小对查询时间的影响

图6 给出了在POI 对象数、查询请求数K和方向关系谓词3 个参数不变情况下,道路网络大小对CDR-CKNN 算法和IMA/GMA 算法CPU 运行时间的对比情况。可以看出,当道路网络规模较小时,2 种算法的CPU 运行时间并没有太大差距；当道路网络规模增加时,2 种算法之间的差距越来越明显,道路网为150K 时,IMA/GMA 算法是CDR-CKNN算法运行时间的2 倍；道路网为250K 时,IMA/GMA 算法是CDR-CKNN 算法运行时间的3.3 倍。这是因为道路网络规模增加时,POI 对象的分布密度(本文用POI 对象数与道路网规模的比值来衡量)降低,IMA/GMA 算法计算最短路径时采用的是盲目扩展方式,需要遍历大量的网络边；而CDRCKNN 算法通过方向关系谓词可以快速过滤掉与查询结果无关的边,大幅缩短计算最短路径的时间。

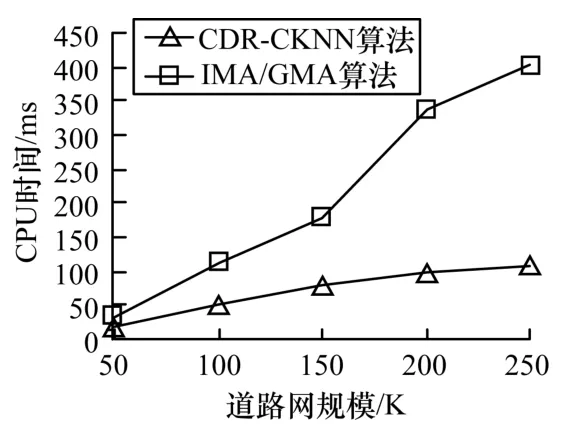
图6 道路网规模对CPU 运行时间的影响

5.2 兴趣点对象数量对查询时间的影响

图7 给出了在道路网规模、查询请求数K和方向关系谓词3 个参数不变情况下,POI 对象数量对CDRCKNN 算法和IMA/GMA 算法CPU 运行时间的对比情况。POI 对象数量决定了对象在道路网络上的分布密度,当POI 数量较少时,道路网上POI 对象分布稀疏,为查询到K个最近邻对象,IMA/GMA 算法需要不断扩展搜索网络,CDR-CKNN 算法也需要不断扩展方向区域的查询半径r,2 种算法的CPU 运行时间都较高；但是CDR-CKNN 算法采用了预计算技术,大大降低了计算最短路径的时间,因此在POI 对象数量为5K 时,CPU 运行时间明显优于IMA/GMA 算法。随着POI 对象数量的增加,2 种算法的CPU 运行时间都减少并呈现出平缓下降的趋势。

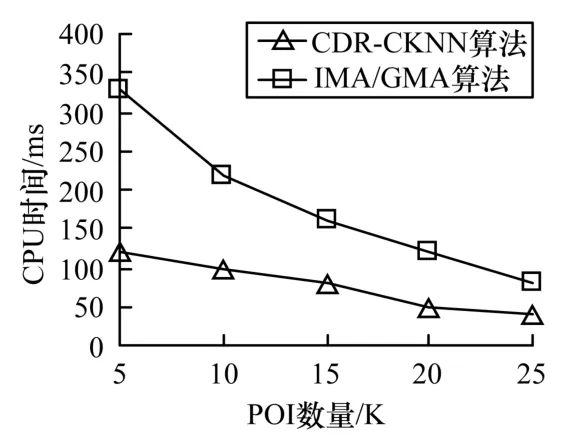
图7 兴趣点对象数量对CPU 运行时间的影响

5.3 方向关系谓词对查询时间的影响

图8 给出了采用四方向模型和八方向模型定义方向关系谓词时对查询算法性能的影响情况。从定义7 可以看出,八方向模型与四方向模型相比,细化了参考对象周围的空间区域,定义的方向关系谓词限制了更小的KNN 查询区域,因此,从图8 可以看出,在相同条件下,八方向模型定义的方向关系谓词查询有更少的CPU 运行时间,并且CDR-CKNN 算法仍然优于IMA/GMA 算法,平均性能提高1.5 倍～3 倍。

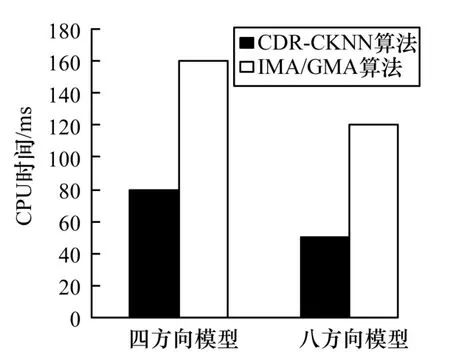
图8 不同方向关系模型对查询性能的影响

6 结束语

本文利用方向关系可以作为空间查询选择条件这一特点,提出基于方向关系谓词约束的道路网络连续K 最近邻查询算法(CDR-CKNN)。为提高KNN 查询速度和更新速度,算法做了3 点改进：(1)将方向关系谓词转化为开放图形区域,与道路网络层进行Intersect 运算,快速过滤掉与查询结果无关的道路边；(2)利用预计算的道路结点之间的最短路径,快速计算查询对象与查询区域内POI 对象之间的最短路径,从而得到K个最近邻对象；(3)建立三层索引结构,将静态的道路网和动态的移动对象分别存储,便于移动对象位置的不断更新。实验结果表明,本文提出的CDR-CKNN 算法的查询性能比IMA/GMA 算法提高2 倍～3.3 倍。今后工作的重点是将方向关系谓词约束与反向最近邻查询相结合,提高道路网络上反向最近邻查询算法的性能。

[1]Kim Hyeong,Chang Jae-Woo.K-Nearest Neighbor Query Processing Algorithms for a Query Region in Road Networks[J].Journal of Computer Science and Technology,2013,28(4)：585-596.

[2]Mouratidis K,Yiu Man-Lung,Papadias D.Continuous Nearest Neighbor Monitoring in Road Networks[C]//Proceedings of the 32nd International Conference on Very Large Data Bases.Seoul,Korea：ACM Press,2005：43-54.

[3]Wang Haojun,Zimmermann R.Location Based Query Processing on Moving Objects in Road Networks[C]//Proceedings of the16th ACM SIGSPATIAL International Symposium on Advances in Geographic Information Systems.Vienna,Austria：[s.n.],2007：143-158.

[4]Demiryurek U,Banaei K F,Shahabi C.Efficient Continuous Nearest Neighbor Query in Spatial Networks Using Euclidean Restriction[C]//Proceedings of International Symposium on Spatial and Temporal Database.Aalborg,Denmark：[s.n.],2009：25-43.

[5]廖 巍,张 琪,吴晓平,等.网络环境下的连续k 近邻查询处理研究[J].小型微型计算机系统,2010,31(4)：666-671.

[6]赵 亮,景 宁,陈 荦,等.面向多核多线程的移动对象连续K 近邻查询[J].软件学报,2011,22(8)：1805-1815.

[7]Shekhar S,Liu Xuan.Direction as a Spatial Object：A Summary of Results[C]//Proceedings of the 6th International Symposium on Advance in Geographic Information Systems.[S.l.]：ACM Press,1998：69-75.

[8]石 静,刘永山.基于开放区域的定量方向关系查询技术[J].计算机工程,2007,33(22)：89-91,94.

[9]郝晓红,张丽平,李 松.三维空间中3DR44 方向关系表示模型[J].计算机工程,2011,37(1)：75-77.

[10]de Almeida V T,Güting R H.Using Dijkstra’s Algorithm to Incrementally Find the k-nearest Neighbors in Spatial Network Databases[C]//Proceedings of 2006 ACM Symposium on Applied Computing.Dijon,France：ACM Press,2006：58-62.

[11]Papadias D,Zhang J,Mamoulis N.Query Processing in Spatial Network Databases[C]//Proceedings of the 29th VLDB Conference.Berlin,Germany：ACM Press,2003：802-813.

[12]Brinkhoff T.A Framework for Generating Networkbased Moving Objects[J].GeoInformatica,2002,6(2)：153-180.