基于布朗桥模型的重要同现模式挖掘

邓 超 ,罗 泽 ,阎保平

(1.中国科学院计算机网络信息中心,北京 100190；2.中国科学院大学,北京 100049)

1 概述

随着传感器网络、全球定位系统(Global Positioning System,GPS)、手持移动设备和射频识别(Radio Frequency Identification,RFID)等设备的普遍应用,大量的移动对象数据被积累下来[1-2]。在此背景下,针对历史轨迹数据挖掘技术的研究成为当前研究的热点,时空模式发现是主要的研究方向之一,包括时空频繁模式挖掘、时空同现模式挖掘和时空关联模式挖掘[3]。然而,在时空数据挖掘的众多模式中,同现模式的挖掘占有重要地位。

同现模式挖掘就是发现在时间和空间上共同出现的时空对象,比如,两只鸟在飞行过程中在同一时间同一地点出现。重要同现模式挖掘就是发现那些在某区域内同时出现并持续足够长时间的时空对象,重要同现模式不仅包括了同现,还限定了同现必须持续一定长的时间,比如,某几个人可能在一起开会,他们会同时出现在会议室并持续一定时间,或者某些动物群体性的迁徙过程中一起出现在某个区域,并停留了很长时间。

同现模式挖掘的研究已经有了比较长的历史。文献[4]提出空间数据的频繁同现邻居挖掘,使用同现位置的对象数量作为支持量来衡量同现位置的重要程度。文献[5-6]提出一种基于Apriori 算法的同现模式挖掘算法框架,使用参与率来取代支持量,这使得同现评价指标更有统计意义。此外,还有基于聚类方法的同现模式挖掘[7-9]。文献[10]提出基于密度的同现模式挖掘,该算法通过将对象分区,优先处理密集分区的样本,减少了Apriori 算法连接次数,提升了效率,但该算法没有考虑时间信息。

基于概率建模的方法一直是时空数据挖掘的重要方式,在经停地挖掘中也有重要应用。文献[11]提出基于核方法的经停地分布建模算法。文献[12]提出使用布朗桥模型来为时空对象的移动数据建模,并应用于经停地挖掘中。文献[13]在该算法的基础上进行改进,提出能够容错的针对时空对象轨迹数据的布朗桥建模。利用概率建模分析经停地的好处是可以通过概率密度来增加对离散采样点数据的鲁棒性,减少因为数据采样间隔时间过长或者采样不完整所带来的误差。

现有的同现模式挖掘只关注了同现的瞬时性,而没有关注同现的持续性。基于概率建模的经停地分析关注点也只在单一的对象上,而没有去挖掘群体性的模式。本文提出重要同现模式挖掘,将同现模式挖掘和经停地分析结合起来,挖掘出具有群体性和持续性特点的时空模式。

2 概念定义及问题描述

首先介绍文中用到的符号定义：时空对象采用小写字母a,b,…表示；时空点由大写字母P表示,P={x,y,timestamp},即P由二维空间的点对(x,y)以及时间维度的采样时间戳timestamp所确定,P(a,τ)表示对象a在时刻τ所处的位置；轨迹TR由某个对象的一系列时空点P组成,并按时间排序,对象a的轨迹TR(a)={P(a,τ1),P(a,τ2),…,P(a,τn)},其中,τ1≤τ2≤…≤τn。

同现实例：一个长度为N的同现实例由来自N个不同对象的N个时空点组成(每个对象一个时空点),并满足条件：(1)任意2 个时空点之间的时间间隔必须小于一个时间阈值thco；(2)任意2 个时空点间的空间距离不得大于一个长度阈值dtco。

重要同现实例：长度为N的重要同现实例来自N个对象的若干个同现实例组成的集合,该集合满足条件：(1)集合中的每个同现实例都是一个长度为N的同现实例；(2)集合中所有同现实例在时间上连续,并且首尾的时间跨度大于一个时间阈值thimco。该集合中的每一组同现实例都是一个重要同现实例。

重要同现实例代表着重要的时空移动模式,例如,鸟群在迁徙过程中集体在某个区域栖息了一段时间,则他们的群体栖息行为可以通过重要同现模式来描述,在鸟群发生禽流感时,通过采样数据,利用挖掘方法得到的群体栖息地,将是发现流感传播途径的重点关注区域。本文需要解决的问题是：给定N个移动对象的空间轨迹采样数据,挖掘任意长度的重要同现实例。

3 重要同现模式挖掘算法

重要同现模式挖掘算法具体如下：

(1) 利用布朗桥为每条轨迹建模,并求得轨迹对应的经停地。

每个移动对象都有各自的一条轨迹,利用布朗桥为对象轨迹对应的概率分布建模,建模方法采用容错的布朗桥模型[13],然后利用该分布得到该时空对象的经停地,这里需要定义一个概率阈值rate,将轨迹的分布概率大于rate的部分,作为经停地。图1(矩形表示轨迹的起点位置,三角形表示轨迹的结束位置)展示了一只斑头雁的时空轨迹图和利用布朗桥模型得到的经停地。

图1 青海斑头雁时空轨迹

(2) 找到2 个对象相交经停地中的重要轨迹。

由于布朗桥建模得到的概率分布没有时间信息,经停地区域中可能包含多条轨迹片段,因此要找出经停地中的重要轨迹。重要轨迹是指满足重要同现要求的对象的连续时空点集合。解决的整体思路是先找到不同对象的共同经停地,然后,再在这个共同经停地内寻找停留时间足够长的对象各自的轨迹,而这些轨迹就是重要轨迹。

算法1求a,b的相交经停地的重要轨迹

1) 找到a,b经停地的空间交集,如果交集为空,返回NA,否则,得到经停地交集STOPOVER,进行第2)步；

2) 定义a,b的重要轨迹集合SET(a),SET(b)；

3) 按时间顺序遍历TR(a)在STOPOVER中的时空点,如果找到一条轨迹片段TRi(a)满足TRi(a)的终点时间τn和起点时间τ0的时间差τn-τ0≥thimco,则将该条轨迹加入到SET(a)中；

4) 按时间顺序遍历TR(b)在STOPOVER中的时空点,如果找到一条轨迹片段TRi(b)满足TRi(b)的终点时间τn和起点时间τ0的时间差τn-τ0≥thimco,则将该条轨迹加入到SET(b)中；

5) 如果SET(a)为空集或者SET(b)为空集,则返回空集,否则返回SET(a)和SET(b)。

经过算法1,就找到满足重要条件,并且在同一个空间区域的轨迹,从而过滤掉了大量不需要做同现实例挖掘的采样点。

由于每个轨迹建模后得到的经停地区域都包含了对应的轨迹所在的位置点,因此重要轨迹必然存在于经停地区域中。此外,同一个对象轨迹的2 条子轨迹也可能存在于同一个经停地中,因此,该算法重新扫描了2 个对象的轨迹,从而保证了经停地中发现的重要轨迹都是原轨迹中的连续采样点。

由于空间交集是数学计算,则求交集部分只需要O(1)复杂度,而找重要轨迹的过程分别需要O(n)的时间复杂度,n是轨迹对应的采样点数目。

(3) 利用2 个对象的重要轨迹,找到重要同现实例。

用类似Apriori 的算法[5-6]来发现同现实例,从长度为2 的同现实例开始,依次连接,长度为N+1的同现实例可以由长度为N的同现实例连接得到,同现实例的判断按照定义判断。方式如下：

算法2寻找N个对象的同现模式

1) 定义集合SET(2)为空集；

2) 对a的每一个重要轨迹TRi(a)：

对b的每一个重要轨迹TRj(b)：

如果TRi(a)和TRj(b)的时间跨度没有重叠,则进入下一个循环；

构造列表LIST为空集；

对TR(a)中的每个时空点Pa：

对TR(b)中的每个时空点Pb：

如果Pa和Pb满足同现实例条件,将(Pa,Pb)加入LIST中,其中,Pa和Pb在对象标记上满足特定的偏序关系；

将LIST中的元素按照时间排序,遍历LIST,如果LIST中存在连续子序列满足时间跨度大于等于thimco,则将子序列记为重要同现实例,将对应的实例加入SEST(2)中；

3) 如果SET(2)为空集,返回空集,否则,进入第4)步；

4)k=3～N：

定义SET(k)为空集,LIST为空集；

对SET(K-1)中的任意2 个元素PA,PB,如果对应的前k-2 个对象相同,即PA[1：k-2]=PB[1：k-2],并且最末2 个对象PA[k-1]和PB[k-1]满足同现实例条件,则将(PA[1：k-2],PA[k-1],PB[k-1])加入LIST中；

将LIST4 中的元素按照时间排序,遍历LIST,如果LIST中存在连续子序列满足时间跨度大于等于thimco,则将子序列记为重要同现实例,加入SEST(k)中；

如果SET(k)为空集,记录下sk=k,停止循环；

5) 返回SET(2),SET(3),…,SET(sk)。

经过算法2,就得到了最终的各长度的重要同现实例。

从Apriori 算法思路可知,采用自底向上的计算方法,能够完全计算出所有长度的重要同现实例。因为,若(PA[1：k-2],PA[k-1])和(PA[1：k-2],PB[k-1])不是重要同现实例,则(PA[1：k-2],PA[k-1],PB[k-1])肯定不满足同现条件,反之,若(PA[1：k-2],PA[k-1],PB[k-1])是重要同现实例,则(PA[1：k-2],PA[k-1])和(PA[1：k-2],PB[k-1])也必然满足重要同现条件。所以,该算法能够保证挖掘结果的完备性和正确性。

虽然该算法基于Apriori 思路,但是计算复杂度不同于传统的Apriori 算法,在连接时,该算法并不需要扫描所有采样点,同时,判断连个点是否满足同现条件时,也只需要做欧氏距离计算和时间差计算,这部分的开销为O(1),而每次一排序需要时间复杂度是O(nlogn),因此,该部分算法总体时间复杂度不超过O(knlogn),k是需要计算的重要同现实例的长度,n是采样点个数。

4 实验结果与分析

4.1 实验数据

为验证算法的可行性,将算法应用在来自青海湖的13 只斑头雁从2007 年3 月-2008 年3 月的时空采样数据上。这些斑头雁被绑定了一个太阳能充电的便携式遥感设备,包括一个传输终端和一个微波遥测终端,可以同时通过Argos 卫星和GPS 接收器进行定位。采样收集到的数据格式如表1 所示。

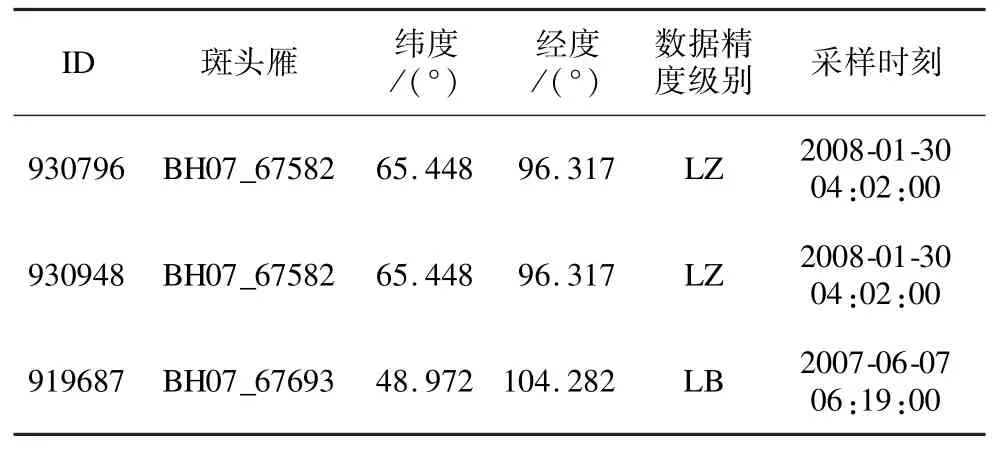
表1 青海湖斑头雁采样数据

为满足实验的精度需求,在原始数据中选择使用误差小于1 000 m 的数据,13 只斑头雁满足要求的数据记录数共22 589 条,为方便距离的计算,将经纬度转换成了坐标。

4.2 实验结果

通过对13 只斑头雁的数据实验发现斑头雁迁徙中的群体移动特点,这些斑头雁在青海湖和西藏之间长途迁徙。青海湖区域、鄂陵湖和扎陵湖区域是迁徙的出发区域,大多数重要同现模式集中在这2 个区域。迁徙的终点主要在错鄂湖区域。除此之外,实验还发现在扎木错区域的重要同现模式,这说明这些斑头雁在迁徙过程中也在这些区域有过群体性的停留。实验发现,对于鸟类分析学家研究鸟类的迁徙模式非常有用,例如这些珍稀动物中出现了传染病,则这些群体性的停留地和停留时间就应当重点关注。图2展示了一组长度为2 的重要同现实例在地图上的位置,该重要同现实例出现在青海湖西北侧(维度37.125°,经度99.731°),时间在2007 年5 月11 日。

图2 长度为2 的重要同现实例在地图上的位置

使用多组参数组合进行实验,通过多组参数的实验,分析不同参数值对实验结果的影响。首先定义了一个参照的参数标准,并列出该组参数情况下的实验结果,如表2 所示。

表2 分组基础参数实验结果

各参数对挖掘出的同现实例数的影响如图3～图6 所示。

图3 同现长度阈值dtco对重要同现实例数的影响

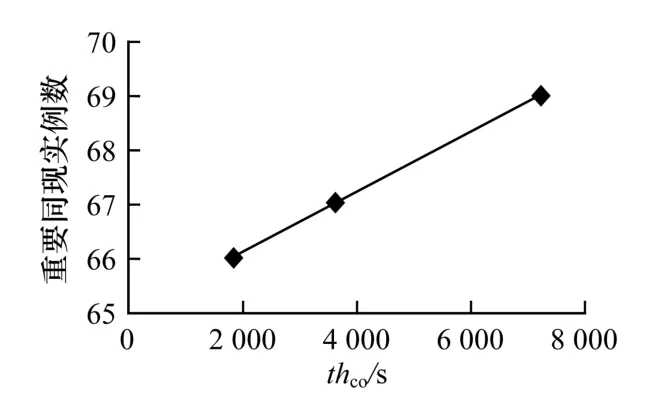
图4 同现时间阈值thco对重要同现实例数的影响

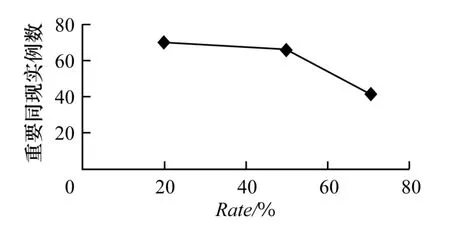
图5 概率密度比例rate 对重要同现实例数的影响

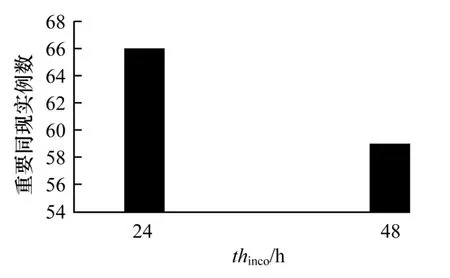
图6 持续时间thimco对重要同现实例数的影响

4.3 参数影响分析

dtco,thco决定了2 个不同的时空点是否是一个同现实例,dtco和thco设定的越大,说明同现条件越宽松,能够找到的同现实例越多,使得重要同现出现的可能增加。

重要同现持续时间thimco决定了一个同现实例集合能不能构成一个重要同现实例,thimco设定的越大,说明对重要性要求越高,越难找到合适的重要同现。算法中在重要轨迹发现和重要同现判断中都使用了该参数,如果该参数比较严格,可能导致dtco和thco的影响力下降,因为该参数也直接决定了同现实例发现所需的候选时空点集合。

概率密度比例rate决定了预先找到的经停地的大小,rate值设置的越大,说明对经停地需要的密度分布越大,那么找到的经停地就越小和越少。在使用该参数时,要考虑到thimco的影响,如果rate选择的太小,导致找到的经停地太小,那么在经停地内就可能不会出现持续时间超过thimco的轨迹,导致找不到重要同现；如果rate取得太大,会使得找到的时空点太多,达不到限制区域和减少冗余计算的目的。

5 结束语

本文通过分析青海湖斑头雁的数据可知,该同现模式算法挖掘出的时空模式具有群体性和持续性的特点,并且研究了算法中各参数间的影响和关系。由于现有同现模式挖掘方法在是否同现的判断上都采用了较武断的阈值,使得同现判断缺少对数据的容错性,概率建模是加强容错性的有效方法,如何直接对同现进行概率建模是下一步研究的方向。

[1]Antunes C M,Oliveira A L.Temporal Data Mining：An Overview [C]//Proceedings of KDD Workshop on Temporal Data Mining.New York,USA：ACM Press,2001：1-13.

[2]Miller H J,Han Jiawei.Geographic Data Mining and Knowledge Discovery [M].Boca Raton,USA：CRC Press,2009.

[3]刘大有,陈慧灵,齐 红,等.时空数据挖掘研究进展[J].计算机研究与发展,2013,50(2)：225-239.

[4]Morimoto Y.Mining Frequent Neighboring Class Sets in Spatial Databases[C]//Proceedings of the 7th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York,USA：ACM Press,2001：353-358.

[5]Huang Yan,Xiong Hui,Shekhar S,et al.Mining Confident Co-location Rules Without a Support Threshold[C]//Proceedings of the 18th ACM Symposium on Applied Computing.New York,USA：ACM Press,2003：497-501.

[6]Shekhar S,Huang Yan.Discovering Spatial Co-location Patterns：A Summary of Results[C]//Proceedings of the 7th International Symposium on Spatial and Temporal Databases.Berlin,Germany：Springer,2001：236-256.

[7]Estivill-Castro V,Lee I.Data Mining Techniques for Autonomous Exploration of Large Volumes of Georeferenced Crime Data [C]//Proceedings of the 6th International Conference on Geocomputation.New York,USA：[s.n.],2001：24-26.

[8]Estivill-Castrol V,Murray A T.Discovering Associations in Spatial Data——An Efficient Method Based Approach[C]//Proceedings of the 2nd Pacific-Asia Conference on Knowledge Discovery and Data Mining.Berlin,Germany：Springer,1998：110-121.

[9]Huang Yan,Zhang Pusheng.On the Relationships Between Clustering and Spatial Co-location Pattern Mining [J].International Journal on Artificial Intelligence Tools,2008,17(1)：55-70.

[10]Xiao Xiangye,Xie Xing,Luo Qiong,et al.Density Based Co-location Pattern Discovery[C]//Proceedings of the 16th International Conference on Advances in Geographic Information Systems.New York,USA：ACM Press,2008：29-34.

[11]Worton B J.Kernel Methods for Estimating the Utilization Distribution in Home-range Studies [J].Ecology,1989,70(1)：164-168.

[12]Billiard F.Estimating the Home Range of An Animal：A Brownian Bridge Approach [D].Chapel Hill,USA：University of North Carolina,1991.

[13]Horne J S,Garton E O,Krone S M,et al.Analyzing Animal Movements Using Brownian Bridges [ J].Ecology,2007,88(9)：2354-2363.