基于瞬时接触线的齿向修形刀位优化方法

方成刚，黄筱调，郭二廓，张 虎

（1.南京工业大学 机械与动力工程学院，江苏 南京 210009；2.南京工业大学 江苏省工业装备数字制造及控制技术重点实验室，江苏 南京 210009）

0 引言

随着齿轮传动向高速、高精度方向不断发展，齿轮齿向修形技术得到越来越多的关注。齿轮齿向修形是齿轮沿齿向方向进行微量的齿面修整，以使其偏离理论齿面。通过齿向修形可以改善载荷沿轮齿接触线不均匀分布的现象，从而大大提高齿轮承载能力。最常见的齿向修形方法有齿端修薄、螺旋角修整和鼓形修形。齿向修形常用的砂轮附加运动方式有附加径向运动（中心距变动）、附加转角运动和附加切向运动等。其中附加径向运动因其在机床上容易实现、附加运动精度高而在实际应用中得到了广泛应用。

关于成形磨齿方面，早期研究主要是砂轮廓形求解及砂轮安装参数调整方面。YOSHINO 等［1-2］通过对砂轮廓形和位置的补偿提出一种成形磨削的齿向修正方法；NISHIDA 等［3-4］通过对砂轮廓形的精确求解提出一种通过调整砂轮安装偏转角的接触线形态优化方法，并将该方法应用于齿向修形；苏建新等［5］采用数值模拟方法对砂轮廓形进行了建模求解。同时，成形磨削修形理论是成形磨齿的一个关键技术，LITVIN 等［6］建立了成形磨削以及展成磨削的数学模型；吴序堂等［7］阐述了渐开线交错轴齿轮建模与加工的相关核心理论；DING 和ZHU等［8-10］基于单参数曲面族包络原理的研究，得到多轴数字控制（Numerical Control，NC）加工的特征曲面在任意刚体运动下扫掠包络曲面的解析表达式。

近年来，随着计算机数字控制（Computer Numerical Control，CNC）技术的发展，成形磨齿技术的研究集中在多轴数控成形磨削修形加工方面。梁锡昌［11］与吉野英弘［4］等研究了三种附加运动方式对齿轮修形的变化规律，并通过综合运用三种附加运动的方法实现了对齿面的模拟修整；SHIH 等［12］基于六轴笛卡尔坐标系数控准双曲面成形磨齿机提出了一种齿向修正理论；随后，SHIH 等［13-14］又提出了一种基于多自由度五轴数控成形磨齿机的高阶修正的齿向修形方法。这种通过多种附加运动或多轴联动的磨削方式，虽然磨齿精度较高，但机床的复杂程度及成本也较大。此外，与多轴数控磨削修形对应的，是单一的附加径向运动齿向修形。李国龙等［15］基于附加径向运动的成形磨削拓扑修形齿轮进行了研究，提出了一种减小磨削误差的砂轮廓形优化方法，但该方法是基于对刀具截形的优化。

传统的斜齿轮鼓形修形采用的是径向等效进刀法，是一种近似的进刀方法，这种方法并没有考虑修形量附加径向运动对瞬时接触线的影响，因为当砂轮有附加运动时，包络面特征线不再是一条空间不变的曲线，而是随着附加运动变化的时变曲线，这种变化使得实际修形齿面在啮合区域发生修形扭曲，尤其是在测量圆（通常取节圆）处存在较大的磨削修形误差。因此，为了进一步提高成形磨齿的修形精度，本文采用较为常用的附加径向运动鼓形修形为研究对象，提出一种刀位轨迹的优化方法，并通过实例对该方法进行了验证。

1 成形磨削斜齿轮齿向修形的数学模型

1.1 圆柱齿轮的鼓形修形

常见齿轮的齿向修形方式有K 形图修形、鼓形修形和点对点修形，不同齿向修形方式在数控成形磨削的本质是一致的。本文选取数学描述较为简洁的鼓形齿向修形齿轮作为研究对象。

修形量ε（z）与z轴的关系如图1所示。对于整齿面鼓形齿而言，可以通过建立圆弧ABC 的方程求解任一轴向坐标值处的修形量。

设齿轮的宽度为b，齿向修缘值在端部为ε（z=0）=ε（z=b）=ε，修形方式为正齿面对称全鼓形修形，由几何关系可得在任意的zi处，齿轮的齿向修形量为

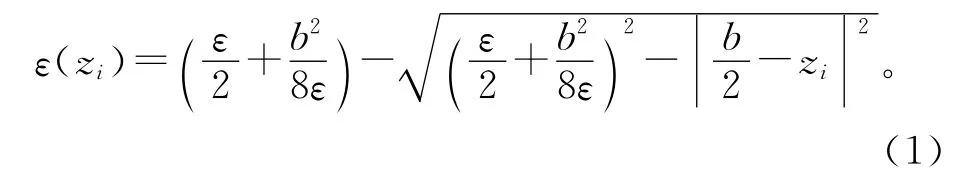
1.2 鼓形修形的齿面方程

齿轮做齿向修形时，可以将齿轮端面截形沿其法矢作等距线。渐开线圆柱齿轮端截形存在以下性质：若渐开线的基圆为rb，则与该渐开线等距rbΔu的曲线仍然是渐开线，并且该等距线相当于将原渐开线绕基圆圆心旋转Δu。因此，可将该渐开线绕基圆圆心旋转Δu，则修形量ε（z）与转角θ的关系为

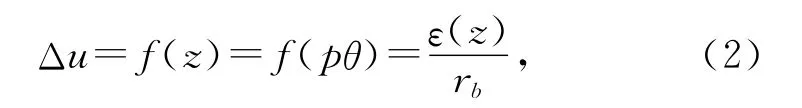
则齿向修形后螺旋面方程为：

式中：τ=σ0+u+θ+Δu，p=pz／2π；θ为端截形上参数为u 的点M 绕z 轴转过的角度；p 为螺旋参数，右旋为正，左旋为负；pz为螺旋导程。

1.3 成形磨削坐标系建立及其变换关系

图2所示为成形磨削修形渐开螺旋齿面的空间关系示意图。建立Ogxgygzg，Oxyz，Owxwywzw三个左手坐标系。其中：Oxyz为空间固定坐标系；坐标系Ogxgygzg与齿轮固连，其轴线为坐标轴zg；Owxwywzw与砂轮固联，其轴线为坐标轴zw，它与z轴负方向之间的夹角为Σ，坐标轴xw与齿轮坐标系的xg轴重合，两坐标系原点间的距离OOg等于中心距a。磨削时齿轮作回转运动，砂轮除了沿齿轮轴线的移动，还有径向的附加运动。因此，Ogxgygzg与Owxwywzw的相对位置可由径向位移ax、安装角Σ及转角θ 表示。开始磨削前即θ=0 时，Oxyz 与Ogxgygzg重合，ax等于砂轮与齿轮的初始轴间距a0，zg=0，a为齿宽中部处的轴间距，Σ 为砂轮安装角（与齿轮螺旋角互余）。

由工件坐标系Ogxgygzg到空间固定坐标系Oxyz 的变换关系为

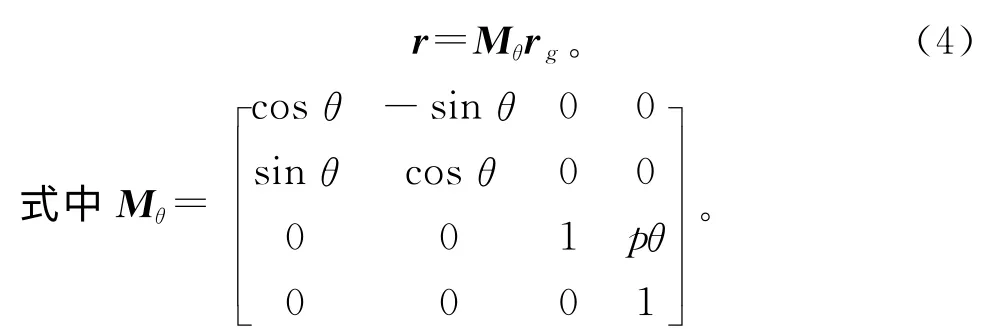
由固定坐标系Oxyz 到砂轮坐标系Owxwywzw的变换关系为

因此从砂轮坐标系Owxwywzw到工件坐标系Ogxgygzg的变换关系为

其中变换矩阵为

2 砂轮廓形的逆包络及B样条逼近

砂轮廓形精度直接影响齿轮成形磨削的精度。刀具路径的优化求解不但要求砂轮离散点足够多，而且要保证迭代求解的效率。因此，本文采用无瞬心包络法求解砂轮廓形，并对求解的砂轮廓形离散点进行B 样条逼近，以实现对砂轮回转曲面的精确控制。

2.1 砂轮廓形的逆包络

利用盘形砂轮无瞬心包络式给出的渐开螺旋面，参考文献［7］给出了砂轮与工件的接触线条件为

接触条件式（7）是参变数u和θ 的关系式，该方程为超越方程，不易求得解析解，可以通过，遍历定义域内参数ui∈［u0，un］，求出相应的θi，将（ui，θi）代入螺旋面方程（3），得到刀具与螺旋面之间的空间接触线离散点矩阵［xi，yi，zi］。

图2建立了盘形刀具坐标系Owxwywzw与工件坐标系Ogxgygzg之间的变换关系，利用该变换关系，将螺旋面上的离散点阵［xi，yi，zi］变换到刀具坐标系中的离散点矩阵［Xi，Yi，Zi］：

将刀具坐标系中的接触线绕刀具轴线旋转一周后，可以得到相应的刀具回转面，取其轴向截形为

2.2 砂轮刀具的回转曲面

由微分几何知识可以求得砂轮截形曲线的控制顶点dj（j=0，1，…，n），用k次B样条曲线表示为

如图3所示，建立刀具坐标系OXYZ，将该曲线绕Z 轴旋转后得到砂轮的回转曲面。任取刀具轴向截形上一点（px（ui），pz（ui）），则刀具回转面方程可表示为

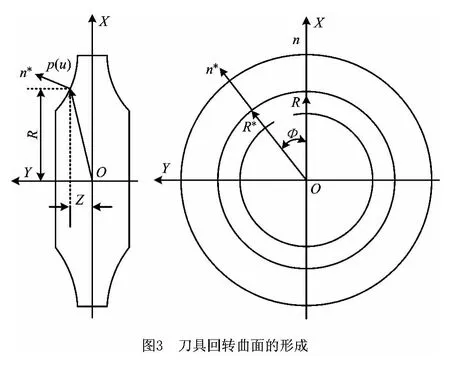
根据刀具曲面方程（11）可知，刀具曲面上任一点对应的径矢R＊可以通过对OXZ 平面内的对应矢量R 绕Z 轴旋转φ 角后得到，该点的法矢n＊同样可以通过对OXZ 平面内相对应的法矢n 绕Z 轴旋转φ 角后得到。则砂轮回转曲面上任一点的径矢和法矢可以表示为：

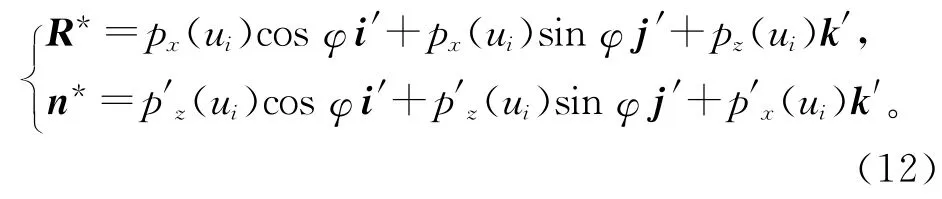
2.3 径向附加运动的砂轮曲面族包络

包络理论在数控加工误差校验、共轭曲面设计中有重要的应用。本文主要采用单参数曲面族的包络理论建立修形后的包络齿面。包络出的齿面是一个单参数曲面族｛Sλ｝，其中λ是参数，当λ的值变化时，得到族中不同的曲面Sλ。

［7］可得一般回转面在任意刚体运动下扫掠包络面的解析表达式。砂轮在欧式空间R3中作刚体复合运动，其连续刚体运动在惯性坐标系中的表示采用下列单参数刚体变换：

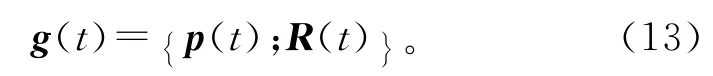
式中：p（t）为与刚体固连的活动标架在惯性坐标系中的平动矩阵；R（t）为与刚体固连的活动标架在惯性坐标系中的旋转矩阵。直角坐标系中的旋转矩阵具有正交性，即满足RTR=RRT=1。

由砂轮坐标系Owxwywzw到工件坐标系Ogxgygzg的变换矩阵，可得对应的旋转矩阵

对应的平动矩阵

砂轮在惯性坐标系（工件坐标系）中的瞬时角速度为

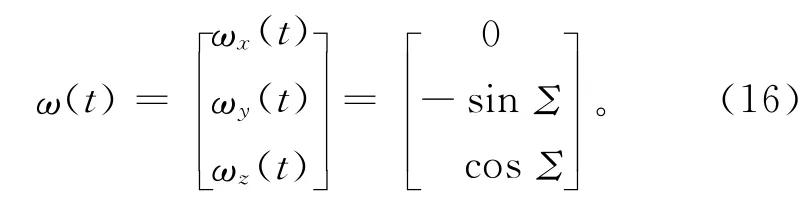
砂轮在惯性坐标系中的平动速度

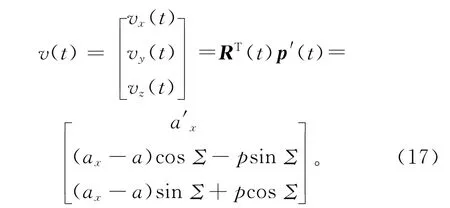
将砂轮回转面的方程式Q（u，φ）与法向量表达式n（u，φ），以及角速度和平动速度代入接触条件式，求得附加径向运动后齿向修形齿面的接触条件为

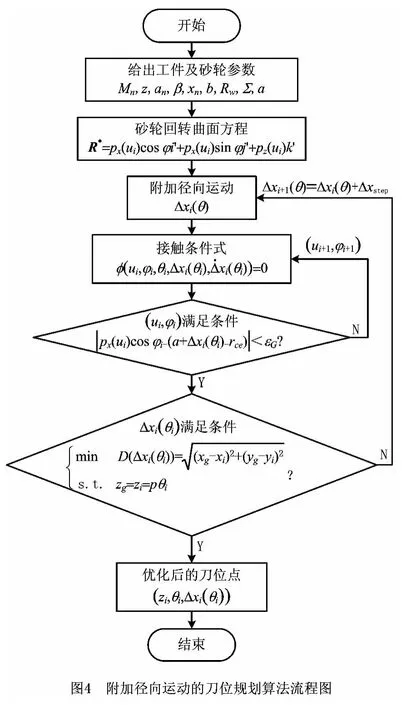
3 附加径向运动的成形磨削刀位规划

径向附加运动的齿向修形通常用于圆柱齿轮的单齿面或双齿面磨削，齿向修形齿轮通常要求齿轮在测量圆处的螺旋线逼近齿向修形曲线，即砂轮曲面族包络曲面与修形螺旋面在测量圆处达到高阶逼近。

3.1 建立刀位规划目标函数

齿向修形螺旋面在测量圆上的测量螺旋线方程为

式中：rm为渐开线螺旋面上的测量圆半径；σm为渐开线螺旋面上的测量圆对应的齿槽半角。

齿向修形齿面要求在砂轮的每个离散刀位上，砂轮特征线（即砂轮与螺旋面的接触线）上处于测量圆处的接触点与螺旋面上处于测量圆处的对应点之间的距离最小。即在每个离散刀位pθi处有径向附加运动Δxi（θi），此时砂轮曲面的特征线与测量螺旋线 在zg=zi=pθi处 满 足D（Δxi（θi））=最小，则相应的刀位点坐标（zi，θi，Δxi（θi））为最优刀位。用数学语言描述上述优化准则为：

3.2 刀位轨迹的确定

当采用附加径向运动进行刀位规划时，不但附加径向运动的位移（即砂轮与工件中心距的变动）会影响接触线位置，而且附加径向的速度也会影响接触线位置。因此，在刀位点寻优时要同时兼顾径向附加运动位移及速度造成的特征线变化。由于接触线条件中的附加运动速度以其一阶导数形式x（θ）出现，难以用解析法直接求解，这里采用有限差分代替径向附加运动的速度x（θ），即

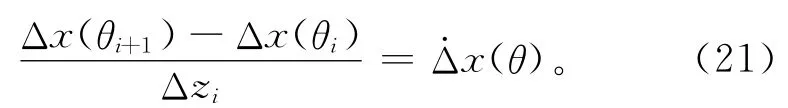
通过寻找适当的径向附加值Δxi（θ），使得砂轮初始刀位的特征线满足上述优化条件，则可得到刀具的优化轨迹。具体的求解过程（如图4）如下

步骤2 遍历砂轮截形的变参量u∈［0，1］，并根据接触线条件求得相应的φi，得到接触线上的一点（ui，φi）满足

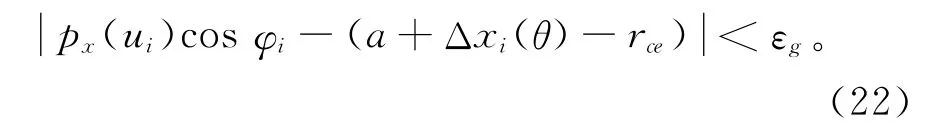
式中εg为砂轮接触点逼近测量圆半径的允许精度。

步骤3 将砂轮接触线上处于测量圆的点转换到工件坐标系中：

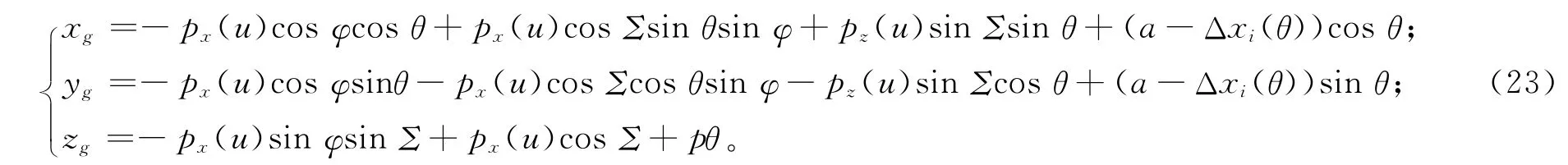
将该砂轮曲面族接触点的轴向坐标值转换到端面中，对应的旋转角

则齿面测量螺旋线位于砂轮特征线在测量圆处接触点的坐标满足式（22）。

步骤4 计算砂轮特征线上处于测量圆半径接触点与相应的齿面测量螺旋线对应点的距离为

对应给定的逼近精度εw，若D＜εw，则相应的Δx0（θ）满足要求；否则，Δxi+1（θ）=Δxi（θ）+Δxstep，重复上述步骤，直至D＜εw。

通过上述4个步骤的循环迭代，可以确定满足精度要求的齿向修形刀位轨迹。最后，综合所有刀位点，得到磨削整个齿面的刀位点（zi，θi，Δxi（θi））。

4 径向附加运动的误差分析

在齿向修形过程中，由于附加运动导致包络面特征线不再是一条空间不变的曲线，而是随着附加运动而变化的时变曲线，这种变化使修形后的齿面产生扭曲变形。通过对比传统的修形方法与文中所提方法的修形误差，可以验证该方法的有效性。下面针对本文所采用的误差评价原理和结论进行讨论。

4.1 砂轮曲面正向包络的求解

将前面求解得到的砂轮截形按所给的优化刀位轨迹进行正向包络，得到相应的包络面方程为：

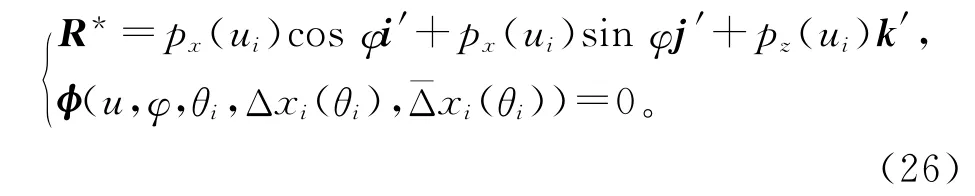
在任一刀位点θi处，利用式（23）可以求出相应的接触线（px（ui）cosφ，px（ui）sinφ，pz（ui））。通 过坐标转换关系式（6）将砂轮瞬时特征线转换到工件坐标系中，可得砂轮曲面族方程为：

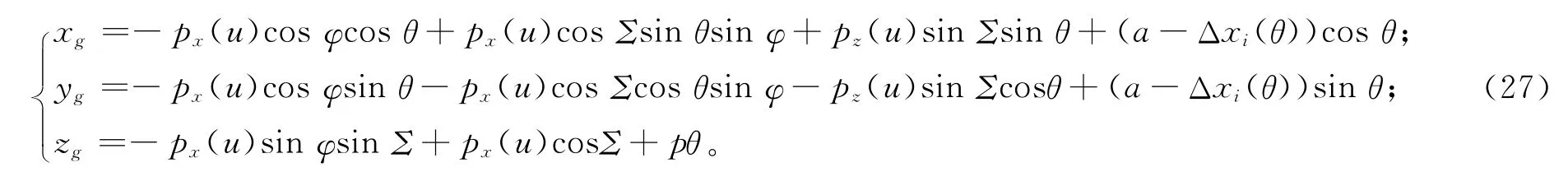
遍历齿轮端截形旋转角θi，得到刀具在不同的轴向位置zi=pθi，按式（27）可求得在该瞬时的砂轮特征线，通过砂轮曲面的正向包络可以得到刀位优化后的包络修形齿面。

4.2 传统修形方法及等高线表示

为了综合表示附加径向运动的齿向修形效果，利用等高线法将整个螺旋面的三维空间修形量及修形误差在平面中表示出来。根据不同齿向变化量将等高线图中的修形量或误差分区进行标志，可以方便地了解修形量或误差在螺旋面上的分布情况。如图5所示，该矩阵以齿轮宽度为横坐标，齿面展开长度为纵坐标，得到一个齿顶在上、齿根在下的齿面展开图。将计算出的齿向修形量用等高线表示在该矩形内，得到修形齿面的等高线表示，图形中部的修形量为0，等高线以5μm 为间隔，如图5左上角（即齿轮的左端齿顶）修形量约为45μm，而右下角（即齿轮的左端齿根）修形量约为10μm。

图6所示为修形量为0.05 mm 时传统的采用单一附加径向运动后的实际齿向修形等高线（单位：μm），此时由于空间接触线的变异，使得修形后的齿面修形量发生扭曲变形，且造成左右修形量不对称，左端过修，而右端欠修。

4.3 两种优化方法对比

为了减小传统的径向等效进刀法在测量圆处造成的齿向修形误差，改善整个齿面修形磨削误差分布，本文采用刀位优化方法，即在砂轮附加径向运动的基础上，通过图4给出的算法流程，动态调整砂轮附加径向进给值，从而得到最优的刀具路径。

将优化后的刀具路径用于实际的齿向修形中，即可减小测量圆处的修形误差，并能改善齿面上磨削误差的分布。图7所示为根据以上算法流程对该工件进行刀位优化后，得到的不同测量圆处的修形误差分布曲线。

图7a所示为当rm=513.42 mm 时，理论修形曲线与实际修形曲线重合，修形误差最小，为Δδ=2 μm；图7b所示为当rm=504.42mm（分度圆）时，修形误差增大，在测量齿面的端部最大值为Δδ=6 μm；图7c所示为当rm=495.42 mm 时，修形误差较大，并在齿根右侧测量齿面的端部达到最大Δδ=12.5μm。

影响不同测量圆处齿向修形误差的不同原因，主要是空间接触曲线上位于测量圆处的点偏离了端平面，偏离端平面的距离越大，修形误差就越大，反之修形误差就越小。例如图7a中测量圆上位于接触线上的点在端面附近，使得修形的误差值最小；图7b和图7c中测量圆位于接触线上的点偏离端面的距离不等，造成的修形误差也不等。

因此，在实际的斜齿轮齿向修形加工中，从理论上来说，若不通过机床和刀具等其他的附加运动，修形误差则难以避免，使得不同测量圆得到的修形曲线不同。为了准确地评价修形曲线是否满足修形要求，应选取合适的测量圆半径，有时测量圆不一定在合理的齿面评价范围内，但为了在合理的齿面评价范围内准确地评价齿向修形精度，可以通过额外的附加径向运动进行刀位轨迹优化，使其在测量圆处满足齿向修形精度评价的要求。

5 磨削实例

待磨削工件为右旋渐开线圆柱斜齿轮，要求齿向做0.05mm 的全鼓形修形。工件具体参数如表1所示。

为了进一步评价采用附加径向运动修形造成的磨削误差，将齿面划分成6×10的矩阵网格形式，每个网格点对应的误差为δi；将实际齿向修形等高线与理论齿向修形等高线进行对比，得到磨削误差的等高线云图。图8a所示为优化前实际的修形误差等高线图（单位：μm），由图可知，位于测量圆（一般取节圆处，这里对应Y=14mm）处的修形误差最大值为7μm，而对于整个齿面来说，在齿宽80%的评价范围内靠近齿向左侧齿根部分的修形误差最大，为11 μm，则整齿面的误差平方和1 642μm2。

表1 工件参数

如图8b所示，通过优化算法对刀具路径进行规化后，得到测量圆节圆处（Y=14 mm）的修形误差等高线为±1μm，即理论的修形曲线与刀位优化后的修形曲线吻合，若不考虑实际磨削中的其他因素干扰，则满足测量圆处的修形精度评价要求。而在齿宽80%评价范围内的靠近齿向左侧齿顶部分的修形误差最大，仅为6μm，比刀位优化前减小了5 μm，此时整齿面的误差平方和，比优化前减少了42.3%。

对比表2可知，采用该方法对刀位进行优化，一方面可以消除测量圆节圆处的修形误差，另一方面可以减小齿面啮合区域的整体修形误差，从而进一步提高齿向修形的精度。

表2 优化前后修形误差对比分析

图9所示为成形磨齿加工及在线测量实验，如图10 所示为齿向和齿廓测量曲线示意图。图中：（A）曲线rce=513.42 mm，（B）曲线rce=504.42 mm，（C）曲线rce=495.42mm。

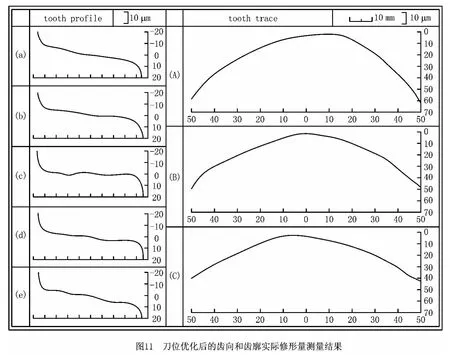
将优化后的刀位轨迹信息输入自主研发的某型成形磨齿机软件中，得到刀位优化后的齿向和齿廓实际修形量测量结果，如图11所示。将对应点的修形量及修形的误差大小与图7进行对比，可得实测值与理论值相吻合，此时测量圆rce=504.42mm处的修形曲线对应于理论修形曲线，吻合度达到90%，且其他测量圆处的误差较优化前减小，从而验证了本文采用的附加径向运动齿向修形刀位规划方法的可行性。

6 结束语

本文从成形磨削的本质出发，研究并求解得到砂轮与工件之间动态的瞬时空间接触曲线，精确地表达了位形空间曲面的动态啮合特性，并采用逆包络法和B样条逼近得到砂轮廓形的回转曲面。

根据单参数曲面包络原理，建立了成形磨削齿向修形误差评价的数学模型。通过对瞬时接触线包络出的修整齿面与理论齿面的误差分析，基于啮合区域误差平方和最小的评价准则，提出一种基于动态调整砂轮附加径向运动轨迹的齿向修形刀位优化方法。

以一种齿向鼓形修形齿轮为例，通过模拟和实验对该方法进行了验证，与传统的径向等效进刀法相比，该方法可有效消除节圆处的修形误差，并可降低整个啮合区域的修形误差，从而提高齿向修形精度。

参考文献：

［1］YOSHINO H，IKENO K，Error compensation for form grinding of gears［J］.Transactions of the Japan Society of Mechanical Engineers Part C，1991，57（543）：3652-3655.

［2］YOSHINO H，IKENO K，Tooth-trace crowning in form grinding of helical fears［J］.The Japan Society of Mechanical Engineers，1991，57（538）：2144-2184.

［3］KOBAYASHI Y，NISHIDA N，OUGIYA Y，et al.Tooth trace modification processing of helix gear by form grinding method［J］.Transactions of the Japan Society of Mechanical Engineers Part C，1995，61（590）：4088-4093.

［4］NISHIDA N，KOBAYASHI Y，OUGIYA Y，et al.Tooth flank modification processing of helical gears by form grinding method［J］.The Japan Society of Mechanical Engineers，1999，65（639）：220-225.

［5］SU Jianxin，DENG Xiaozhong，REN Xianzhong，et al.Form grinding wheel dressing and simulation for helical-gear［J］.Transactions of the Chinese Society for Agricultural Machinery，2010，41（10）：119-222（in Chinese）.［苏建新，邓效忠，任显忠，等.斜齿轮成形磨削砂轮修形与仿真［J］.农业机械学报，2010，41（10）：119-222.］

［6］LITVIN F，FUENTES A.Gear geometry and applied theory［M］.2nd ed.Cambridge，UK：Cambridge University Press，2004.

［7］WU Xutang.Principle of gearing［M］.2nd.ed.Xi'an：Xi'an Jiaotong University Press，2009（in Chinese）.［吴序堂.齿轮啮合原理［M］.2版.西安：西安交通大学出版社，2009.］

［8］DING Han，ZHU Limin.Geometric theories and methods for digital manufacturing of complex surfaces［M］.Beijing：Science Press，2011（in Chinese）.［丁 汉，朱利民.复杂曲面数字化制造的几何学理论和方法［M］.北京：科学出版社，2011.］

［9］ZHU Limin，ZHENG G，DING Han.Formulating the swept envelope of rotary cutter undergoing general spatial motion for multi-axis NC machining［J］.International Journal of Machine Tools and Manufacture，2009，49（2）：199-202.

［10］ZHU Limin，ZHENG G，DING Han，et al.Global optimization of tool path for five-axis flank milling with a conical cutter［J］.Computer-Aided Design，2010，42（10）：903-910.

［11］LIANG Xichang，SHAO Ming，YOSHINO H，et al.，Research on gear and its tool manufacture［M］.Chongqing：Chongqing University Press，2001（in Chinese）.［梁锡昌，邵明，吉野英弘，等.齿轮及其刀具制造的研究［M］.重庆：重庆大学出版社，2001.］

［12］SHIH Y，FONG Z.Flank correction for spiral bevel and hypoid gears on a six-axis CNC hypoid gear generator［J］.Journal of Mechanical Design，2008，130（6）：062604.

［13］SHIH Y P，CHEN S D.A flank correction methodology for a five-axis CNC gear profile grinding machine［J］.Mechanism and Machine Theory，2011，47（1）：31-45.

［14］SHIH Y P，CHEN S D.Free-form flank correction in helical gear grinding using a five-axis computer numerical control gear profile grinding machine［J］.Journal of Manufacturing Science and Engineering，2012，134（4）：041006.

［15］LI Guolong，LI Xianguang，LIU Fei，et al.Method of profile optimization of a form grinding wheel for grinding with additional radial motion of topologically modified gear［J］.Chinese Journal of Mechanical Engineering，2011，47（11）：155-162（in Chinese）.［李国龙，李先广，刘 飞，等.拓扑修形齿轮附加径向运动成形磨削中的砂轮廓形优化方法［J］.机械工程学报，2011，47（11）：155-162.］