基于多目标猫群算法的混流装配线排序问题

刘 琼，范正伟，张超勇，刘炜琪，许金辉

（华中科技大学 数字制造装备与技术国家重点实验室，湖北 武汉 430074）

0 引言

在混流装配线用于平衡工作站负载的指标中，最小化总超载时间［1］这一经典指标忽略了机器闲置时工人的等待成本，Tavakkoli-Moghaddam［2］在其基础上进一步考虑了不同工作站内设备资产价值、加工速度等对制造系统的影响，对不同工作站上的超载成本赋予了不同的权重。Fattahi［3］综合考虑了正规工人的等待时间和辅助工人的工作时间对工作站负载平衡的影响，提出最小化闲置／辅助工作总成本的目标，然而研究中分别将不同工作站上的正规工人闲置成本和各辅助工人的工作成本设置为相同，不符合不同岗位工人工资差异的实际情况。因此，实际生产过程中考虑不同工作站上工人闲置／超载成本差异的最小化工作站闲置／超载总成本指标，既能平衡工作站的负载，又能优化工人的工作成本，使其与企业的生产实际更加吻合。

目前，混流装配线排序问题的求解普遍采用遗传算法［4-8］和粒子群算法［9-10］，其中：遗传算法同时使用多个搜索点进行搜索，具有隐含的并行性和良好的全局搜索能力，但是搜索速度较慢，易陷入局部最优，导致过早收敛；粒子群算法的可调参数少、收敛速度快，但是在处理离散的优化问题时表现不佳，不能很好地跳出局部最优［11］。Shu-Chuan Chu受猫日常行为动作的启发，于2006年提出了猫群优化（Cat Swarm Optimization，CSO）算 法［12］。CSO 算法的最大特征表现为在进化过程中能够同时进行局部搜索和全局搜索，使其拥有克服遗传算法局部搜索能力不足和粒子群算法求解离散问题时容易陷入局部最优点的能力，且具有很好的收敛速度［13］。猫群算法在连续函数优化［12-16］和 图像处理［11，14，17-18］中得到了良好的应用，证明了它具有比遗传算法和粒子群算法更优异的算法性能，但是还未见到在调度领域中的应用实例。把CSO 算法应用于混流装配线排序，需要将其离散化。本文针对目前CSO 算法在进化过程中一般采用固定的混合比率进行猫行为模式的选择方法，不能根据进化的程度有效分配全局猫和局部猫的数目，提出一种基于线性混合比率的猫行为模式选择方法；针对CSO 算法在搜寻过程中可能出现重复的候选个体，不能有效进行全局搜索，提出基于多样化搜寻算子的改进搜寻模式，用来生成有效的、分布均匀的搜寻结构并进行优化。

1 多目标混流装配线排序问题

1.1 问题描述

本文描述的混流装配线是一种以常速vc移动的传输系统。相似度较高的M 种产品以固定的投放间隔γ 投放到装配线上，每种产品的生产量分别为D1，D2，…，DM。装配线被分成J 个工作站，每个工作站的工位长度Lj固定，且为闭式工作站。正规工人只能在工作站的限定范围内工作，不能穿越它所在工作站的上游边界和下游边界，不能完成的工作交给辅助工人完成，以避免由工作负载引起的生产线的停线。工人对一个产品执行装配任务并随传送带一起移动到下游，完成装配工序或移动到工作站边界后，工人移向上游继续装配下一产品。采用Bard在文献［1］中提出的最小工作循环（Minimal Product Set，MPS）策略组织装配车间的生产。MPS代表混流装配线上要加工产品的向量，（d1，d2，…，dM）=（D1／h，D2／h，…，DM／h），其中：dm表示装配线在一个时间周期内生产m 类型产品的数量，Dm表示在整个计划周期内m 类型产品的装配数量，h是D1，D2，…，DM的最大公约数。模型参数如下：

（1）全局变量

i为产品，i∈｛1，2，…，I｝；j 为工作站，j∈｛1，2，…，J｝；m 为产品类型，m∈｛1，2，…，M｝。

（2）输入参数

αj为第j个工作站等待的时间成本；βj 为第j个工作站超载的时间成本；I 为被排序产品的总数目，；M 为最小工件集中的产品类型数目；Lj为工作站j的长度；tmj为m（m ∈｛1，2，…，M｝）类型的产品在工作站，j（j∈｛1，2，…，J｝）上装配的时间；w 为固定投放率条件下两产品之间的投放距离。

（3）决策变量

xim表示若排序序列中第i 个产品的类型是m则为1，否则为0；Zij表示第i 个产品在第j 个工作站上开始装配的位置；Iij表示第i 个产品在第j 个工作站上的闲置时间；Uij表示第i 个产品在第j 个工作站上的辅助时间。

1.2 优化目标

考虑实例企业平衡工作站负载，减少产品库存量和降低刀具、夹具频繁更换对工人操作技巧的要求，建立改进的最小化超载／闲置总成本、最小化产品变化率和最小化产品总切换时间的多目标混流装配线排序模型。

（1）最小化工作站闲置／超载总成本

传统的平衡工作站负载的模型中，一般都假设不同工作站上的正规工人闲置成本和辅助工人的工作成本分别相同［3］，而实际企业中，工人的操作技巧有高有低，各工作站上工人的工作成本不完全相同。因此对不同工作站上的工人赋予不同的工作成本，得到改进的最小化工作站超载／闲置总成本指标，在平衡工作站负载的同时优化工人的工作成本，以贴近企业生产实际。本文改进了可变投放间距下的最小化闲置／辅助工人成本指标［3］。

其中：式（2）确定混流装配排序序列中每个位置都分配有一个确定的产品；式（3）满足单个生产循环中每种类型产品的需求数量；式（4）强制要求每个循环的第一个产品在工作站的左边界开始；式（5）计算工人在工作站j开始加工第（i+1）个产品的位置；式（6）计算在工作站j上，当第i个产品不能完成时需要辅助工人工作的时间；式（7）表征排序中最后一个产品需要的辅助工人工作时间；式（8）给出工件没有到达时正规工人的闲置时间。

（2）最小化总产品变化率

准时生产（Just in Time，JIT）制造系统的一个基本要求是保证连续和稳定的零部件供应，它能够避免上游生产线产量的波动和减少产品的库存量。

式中Xlm表示产品序列中第1位～第l位产品m 的累积数量。

（3）最小化产品间总切换时间

在混流装配线生产过程中，不同产品需要的工装或工装的设置不同，从一种产品调整到另外一种产品需要调整刀具和夹具，并且有些工装的设置时间与切换顺序有关。因此不同品种产品之间的总切换时间与生产排序有关。

式（10）中，cimr表示工作站J 上从m 类型产品调整到r 类型产品的转换成本，若m 类型产品和r类型产品分别分配给第i 个和第（i+1）个工作，则ximr=1，否则为0。式（11）确定混流装配排序中每个序列有一个确定的产品，式（12）和式（13）保证每个生产节拍中产品的序列不发生变化。式（14）限制一个生产循环中某类型产品的总需求满足MPS。

2 改进的多目标猫群优化算法

CSO 算法通过分组—混合机制进行信息的传递，即采用混合比率将进行搜寻模式和跟踪模式的两个子群猫组合在一起形成种群，在每次迭代过程中采用分组方法重新随机选择猫的行为模式，不同子群采取不同的模式进行更新。搜寻模式中通过对个体自身进行搜寻操作，生成一系列子代填满搜寻记忆池，并用搜寻记忆池中的最好个体更新当前个体，在算法中执行全局搜索的任务；跟踪模式类似于粒子群算法，利用全局最优的位置来更新猫的当前位置［14］。CSO 算法混合了进行全局搜索和局部搜索的两个子群，使得在算法进化的每一代中能同时进行全局搜索和局部搜索，这种独特的算法结构保证了算法的收敛速度和Pareto解的搜索能力，能够克服遗传算法搜索速度慢、容易陷入局部最优、粒子群算法求解离散问题不能跳出局部最优点等缺陷。将求解连续问题的标准CSO 算法应用于混流装配线排序这类离散问题时，需将算法离散化；考虑到CSO 算法现有搜寻算子生成方法单一且可能产生冗余操作，提出了基于多样化算子的改进搜寻模式；考虑到标准CSO 算法搜索猫和跟踪猫固定的混合比率在进化过程中不能有效地分配全局搜索和局部搜索能力，提出了基于线性混合比率的猫行为模式选择方法，改进的多目标猫群（Improved Multi-Objective Cat Swarm Optimization，IMOCSO）算法如图1所示。

2.1 离散化编码和解码操作

标准CSO 算法的连续编码方式不适合求解离散化的混流装配线排序问题，因此需要将标准CSO算法离散化，使得离散编码序列与猫移动过程中的连续位置对应起来。采用随机数表示法［9］和基于工件的编码方法将标准CSO 算法离散化，并采用降序映射规则进行解码。离散化编码步骤为：①为染色体的每个基因生成服从（0，1）均匀分布的随机数，形成一个随机数序列；②按照各维数值大小进行降序排序；③根据离散数字编码和产品类型之间的对应关系进行解码，得到解码序列。假设有A，B和C三种产品，MPS为（3，2，3），离散化编码如图2所示。

2.2 基于线性混合比率的猫行为模式选择方法

CSO 算法采用分组—混合机制控制着算法的进化。在算法的每一次迭代过程中采用混合比率将种群分组，得到搜寻猫子群和跟踪猫子群，对不同子群的猫采取对应的行为模式进行处理；将执行全局搜索的搜寻猫子群和执行局部搜索的跟踪猫子群进行混合形成种群，直到满足算法的终止条件。由此可见，混合比率影响CSO 算法的整体性能，然而标准CSO 算法采用固定混合比率的方法进行猫行为模式选择，即每一代种群中进行全局搜索的搜寻猫和进行局部搜索的跟踪猫的数量比例都是一定的，不能根据算法的进化程度调整全局搜索和局部搜索的比重。在CSO 算法中，若在算法运行前期采用较大比率的跟踪猫可提高算法的全局搜索能力，则可加快算法收敛到Pareto前沿的速度；若在算法的后期采用较大比率的搜索猫，则可提高算法的局部搜索能力，有效地搜索出非支配解，提高解的质量，保证算法的收敛性质。因此，本文提出一种基于线性混合比率的猫行为模式选择方法，如图3所示。算法开始采取较大的混合比率MR1，迭代到最大次数T0时混合比率为MR2。在算法的整个运行过程中，通过调整混合比率来调整算法进行全局搜索和局部搜索的猫的比重。

该线性混合比率的计算公式为

2.3 基于多样化搜寻算子的改进搜寻模式

搜寻模式对应于优化问题的全局搜索技术，通过对当前个体进行搜寻操作，生成填满搜寻记忆池的一系列个体。评价搜寻记忆池中的个体，并用搜寻记忆池中的Pareto非支配解更新当前解。图4给出了应用于混流装配线排序问题的标准CSO 算法搜寻算子。其中产品数目为8，给定改变基因位数（Counts of Dimension to Change，CDC）的范围为［0，8］，生成的改变基因位数的数目为4，随机选择2，4，6，7这4个位置，给定变化域（Seeking Range of the selected Dimension，SRD）为［0，0.15］，生成服从该变化域的4 个随机数0.08，0.14，0.11，0.01，与随机数编码上对应位置的数值相加，得到新的随机数序列，重新按降序排序可得新的解码序列。将标准猫群搜寻模式下搜寻记忆池中候选个体的生成方法称为标准搜寻算子，图4给出了标准搜寻算子的操作过程。

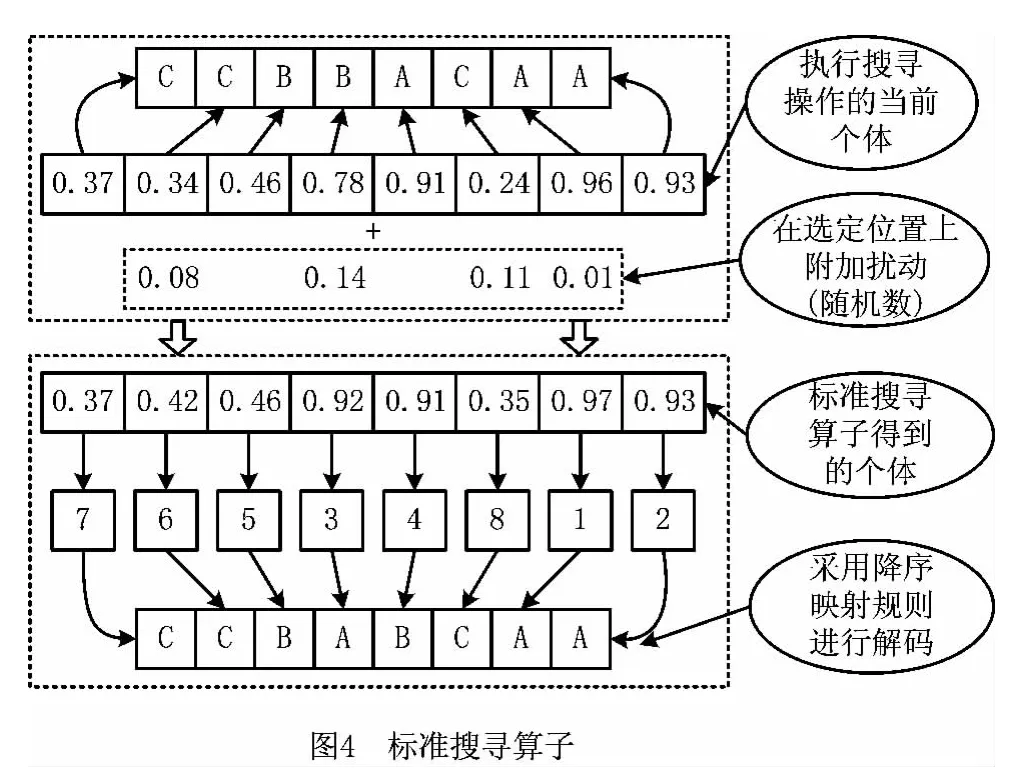
搜寻模式下参数（CDC，SRD）的设置对搜索性能有显著的影响。若参数设置过大，则解的变化范围过大，算法容易变成简单的随机搜索，不利于算法的收敛；若参数设置过小，则解的变化范围小，算法的搜索能力较弱，容易陷于局部最优［11］。尤其在离散问题的求解过程中，算法设置过小，可能得不到有效的候选个体。以图4为例，假设只在第一个基因0.37上发生变异，变异的大小为0.02，按照降序排列的映射规则解码，变异后个体上的基因位置保持不变，该操作即为冗余操作。为了降低算法参数设置对搜寻模式性能的影响和得到分布均匀与多样化的候选个体，提高算法的收敛速度，标准搜寻算子联合遗传算法的三种变异算子组成多样化的搜寻算子，对搜寻模式进行了改进。多样化算子中各算子对应的概率在算法的开始之前设定。

（1）成对交换搜寻算子 随机选择两个任意的产品，其位置分别为i和j（i≠j），交换对应基因上的产品和编码数字，如图5所示。

（2）插入搜寻算子 移动位置i上的产品插入到位置j 后（i≠j），生成新个体，如图6所示。

（3）倒序搜寻算子 随机选择个体的一部分，并将其执行倒序操作，如图7所示。

2.4 跟踪模式

跟踪模式对应于搜索问题的局部搜索技术，采用速度—位移模型，类似于粒子群算法。定义第i只猫在D 维空间中的位置和速度分别为Xi=（Xi1，Xi2，…，XiD）和Vi=（Vi1，Vi2，…，ViD），其中d（1≤d≤D）代表维数。猫群全局最优位置表示为Xg=（Xg1，Xg2，…，XgD）。跟踪模式分以下五步进行工作：

（1）根据式（16）计算第i只猫的新的速度。

式中：w为惯性权重，c为加速度常数，r为服从［0，1］均匀分布的随机数。全局最优Xg从Pareto外部存档解集中随机选取。

（2）根据式（17）计算下一单位时间第i只猫的新位置。

（3）如果第i只猫的新位置中任一维的位置超出了搜索空间，则将该值作为相应的边界值，对应维数的速度乘以-1，从反方向继续搜索。

（4）用基于Pareto分层—小生境技术评价猫的适应度值。

（5）用非支配解的猫的位置更新外部的Pareto存档。

2.5 基于Pareto分层—小生境技术的选择操作

采用Pareto分层—小生境技术进行多目标处理，即在种群进化过程中，采用Pareto分层—小生境评价个体多目标函数值并进行选择，小生境维持种群的多样性。在算法中，设置一个Pareto存档存放每一代运行得到的Pareto解，并用搜寻模式和跟踪模式下得到的当前Pareto 最优解更新Pareto存档。

（1）非支配解排序

对种群各个体进行Pareto非支配解排序，确定各个体Pareto层次。

Pareto支配关系为当且仅当∀j∈｛1，2，…，n｝，fj（x1）≤fj（x2）且∃k∈｛1，2，…，n｝，fk（x）＜fk（x），解x1支配解x2，表示为x1≺x2。

图8所示为两个目标最小化优化问题的Pareto分层示意图，处于第一层即实心标识的点为Pareto最优点，实心点构成的集合为Pareto最优解集，实心点在解空间中的表现形式即为Pareto前沿。分层步骤为：①在当前种群中找出阶层最高的Pareto非支配解集S1，令S1的Pareto层次rank=1；②在余下的个体中找出非支配解集S2；③重复①～②，直至找出阶层最低的非支配解集Slowest才结束。在选择的过程中，阶层高的个体优于阶层低的个体，S1≺S2≺…≺Slowest。

（2）小生境距离计算

采用小生境距离保证非支配解的分布性和多样性，进一步降低算法的早熟收敛，从而增强算法搜索Pareto最优解的能力。假设一个n 目标的问题，MAXlt和MINlt分别为第t 代个体的第l 个目标值的最大值和最小值，popSize 为种群大小。用式（18）计算第l个目标的小生境大小：

当每一个小生境立方体大小相同时，解的拥挤度用立方体中解的个数衡量，个数越多，拥挤度越大。拥挤度小的解赋予较大的概率进化到下一代。

（3）基于Pareto分层—小生境技术的选择机制

种群记为P（t）=｛p1，p2，…，ppopSize｝，排序层次为v的个体记为p（v），当前种群记为Pu，如第一代种群表示为P1。具体步骤为：①初始化参数，Pu=P（t），u=1，因尚未对种群进行Pareto排序，此时所有个体的排序层次v=0；②计算当前种群P（t）内个体的小生境距离；③对种群进行Pareto排序，寻找第u 个Pareto分层PSu，PSu=｛（pi，bi）｝，其中pi为种群Pu的非支配解，bi为pi的小生境距离；④按照bi升序的方式排序PSu中的个体，将rank（v+s）分配给第s个个体，其中，如果Pu≠∅，则返回③，否则进入⑥；⑥通过式prob（p（v））=q（1-q）v-1，v=1，2，…，popSize，确定每一Pareto分层中个体选择到下一代中的概率，式中q 为选择概率参数。

3 算法测试及实例求解

3.1 算法测试

为验证算法性能，采用Mansouri［4］提出的混流装配线排序的小规模和大规模测试集，分别如表1和表2所示。装配线上的操作时间tmj、工作站长度Lj、切换时间cimr分别服从均匀分布U（4，9）、U（12，15）和U（1，3）。将IMOCSO 与第二代非支配排序遗传算法［19］（Non-dominated Sorting Genetic Algorithm-Ⅱ，NSGA-Ⅱ）、多目标粒子群算法［20］（Multi-Objective Particle Swarm Optimization，MOPSO）、第二代强度Pareto进化算法［21］（Streptococcal Pyogenic Exotoxin 2，SPEA2）进行了对比。所有算法的运行环境为2.0GHz Pentium CPU，1G RAM，Windows XP，采用VC++6.0编程，并使用以下指标对各算法进行综合比较：

表1 小规模问题集

表2 大规模问题集

（1）解集覆盖度指标（Set Coverage Metric，SCM）测量已经得到的非支配解集和Pareto最优解集之间的解的相对分布。

（2）世代距离（Generational Distance，GD）计算在Pareto解集中找到的非支配解的平均距离。世代距离越小，表明越收敛于Pareto前沿。

（3）Pareto 前沿最大误差（Maximum Paretooptimal Front Error，MFE）度量di中的最大值。di为第i个解与Pareto解集中距离此解最近的解的欧几里得距离。

（4）分布度指标（Spacing Metric，SM）计算得到的非支配前凸面内连续解的相对距离，用来评价解集在目标空间中的分布情况。分布度指标越小，表明解的分布越均匀。

（5）非支配解的数目（the Number of Non-Dominated solutions，NNDS）算法搜索Pareto前凸面的能力，数目越大说明越易于搜索出Pareto解，即搜索Pareto前沿的能力越强。

为便于各算法的比较，算法参数设置尽可能相同并采用相同的种群规模和迭代次数。CSO 算法相关参数设置为：①小规模问题中，猫的数目为150，SMP=20，MR1=0.6，MR2=0.4，运行100代。②大规模问题中，猫的数目为450，SMP=35，MR1=0.7，MR2=0.3，运行600 代。各算法取20次运行结果的平均值进行各指标的对比，如表3所示，图9～图13 图示化地比较了IMOCSO，NSGA2，SPEA2，MOPSO 的各性能指标。

由图9可知，IMOCSO 的解集覆盖度指标小于其他算法，且在大规模问题中该指标增加缓慢，表明IMOCSO 得到的非支配解能更好地收敛到Pareto最优解集，其收敛性优于其他算法。由图10可知，IMOCSO 的世代距离指标整体优于其他算法，且大规模问题中的结果在减小，表明在各算法设置的相同的迭代次数中，IMOCSO 比其他算法拥有更快的收敛速度。由图11 可知，IMOCSO 算法的误差率小于其他算法，表明该算法能更好地收敛于Pareto前沿。由图12 可知，IMOCSO 算法的分布度指标明显小于其他算法，表明该算法有更好的分布性。由图13可知，IMOCSO 搜索到的非支配解的数目均比其他算法多，表明该算法更容易得到Pareto最优解，算法具有良好的全局搜索能力和局部搜索能力。

表3 各算法性能指标的平均值比较

续表3

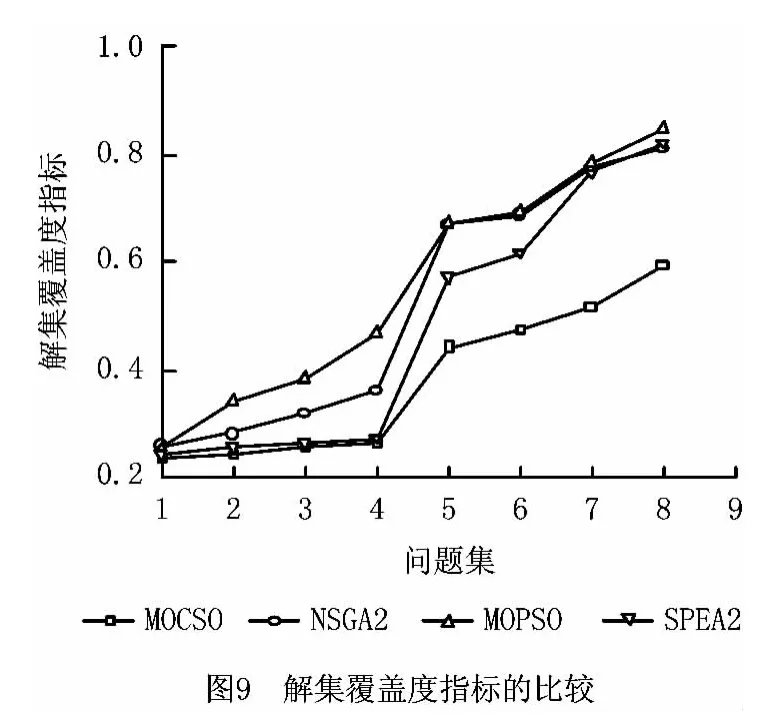
综上所述，IMOCSO 算法在除运行时间之外的指标上都有良好的表现，优于NSGA2，MOPSO 和SPEA2，在大规模问题中表现尤为明显，表明MOCSO 算法能够有效地求解混流装配线排序问题。

3.2 实例验证

为进一步验证IMOCSO 算法的实用性，以及应用提出的改进的多目标混流装配线的数学优化模型，用该算法求解某空调企业的中央空调混流装配线的排序问题。装配线上产品的投放间距W=775 mm，装配线的移动速度为Vc=10 mm／s。需要装配6种四出风室内机产品，日计划产量分别为A 产品45台、B产品90台、C 产品75台、D 产品60台、E产品60台、F 产品90台，最小生产循环MPS为（3，6，5，4，4，6）。经过简单的作业规划合并后，该混流装配线包括装电机、装风轮、装电控、装蒸发器、装送风部件、主打包（贴标签、装附件）6个主要工位。各机型在每个工位上的加工时间经过多次测量求平均值，以确保数据的准确度、减小误差，处理后的数据如表4所示，各工位的长度为产品间的切换时间（如表5），由混流装配车间提供装配线设计数据得到。算法的相关参数设置为：猫的数目为120，SMP=20，MR1=0.6，MR2=0.35，运行100代。算法运行得到53个非支配解，表6所示为部分结果。

表4 模型数据表格

表5 产品间切换平均时间 s

表6 Pareto最优解集

续表6

车间采用生产比倒数法得到的排序为BFCDEABFCDEBFCABFDECBFBFCDEA，目标值分别为137，8.6，405。表6中的结果采用CSO 算法求解得Pareto解集。可以明显看出，表6中的结果支配生产比倒数法得到的结果，这是因为生产比倒数法是侧重于优化产品变化率的启发式规则，不能优化工作站负载和产品切换成本。表6为车间决策提供了多样化的选择，当车间对产品之间的切换有较高限制时，可以选择2，51，52，53号排序序列作为装配线的生产方案；当车间更侧重于平衡工作站负载时，可以选择1，3～8号解；当车间需要低库存、更快响应客户订单时，可以选择较小产品变化率的解，如1，4，6号解。无论以哪种目标为主进行选择，表6 中的解在其他两个目标值上都不会太差。本文所提算法已应用于求解该中央空调的混流装配线排序问题。

4 结束语

本文提出了考虑不同工作站上超载／闲置成本差异的最小化超载／闲置总成本目标，建立了改进的最小化超载／闲置总成本、产品变化率和产品总切换时间的混流装配线排序的多目标数学优化模型，并设计IMOCSO 算法进行求解。将标准CSO 算法离散化应用于混流装配线排序问题；为了提高算法前期的全局搜索能力和后期的局部寻优能力，提出基于线性混合比率的猫行为模式选择方法；为了解决算法应用于混流装配线排序问题中出现的冗余操作的问题，提出一种多样化的搜寻算子。采用五个常用的多目标评价指标对基准案例中的小规模、大规模问题集分别进行测试，并与三种传统的算法MOPSO，NSGA2，SPEA2进行比较，以测试算法的性能。结果表明，本文提出的IMOCSO 算法在求解混流装配线排序问题中具有良好的性能，尤其在处理大规模问题时算法的收敛速度明显。在实例验证部分，将该IMOCSO 算法应用于某空调企业的混流装配线排序问题。

本文为探索和解决CSO 算法在混流装配线排序问题中的应用进行了尝试，并为解决其他调度问题，如作业车间调度、流水车间调度应用中的问题提供了借鉴和帮助，具有重要的理论意义。下一步工作将研究建立更加符合生产实际的混流装配线模型，如随机型混流装配线排序模型，以减小原始数据误差对优化结果的影响，即得到鲁棒性较高的排序方案；测试猫群算法在更大规模问题中的求解性能，以用于更大规模实际问题的求解，如产品类型更多、工作站数目更大的排序问题。

［1］BARD J F，DAR-ELJ E，SHTUB A.An analytic framework for sequencing mixed model assembly lines［J］.International Journal of Production Research，1992，30（1）：35-48.

［2］TAVAKKOLI-MOGHADDAM R，RAHIMI-VAHED A.Multi-criteria sequencing problem for a mixed-model assembly line in a JIT production system［J］.Applied Mathematics and Computation，2006，181（2）：1471-1481.

［3］FATTAHI P，SALEHI M.Sequencing the mixed-model assembly line to minimize the total utility and idle costs with variable launching interval［J］.The International Journal of Advanced Manufacturing Technology，2009，45（9）：987-998.

［4］MANSOURI S A.A multi-objective genetic algorithm for mixed-model sequencing on JIT assembly lines［J］.European Journal of Operational Research，2005，167（3）：696-716.

［5］AKGÜNDÜZ O S，TUNALI S.An adaptive genetic algorithm approach for the mixed-model assembly line sequencing problem［J］.International Journal of Production Research，2010，48（17）：5157-5179.

［6］HYUN C J，KIM Y，KIM Y K.A genetic algorithm for multiple objective sequencing problems in mixed model assembly lines［J］.Computers &Operations Research，1998，25（7／8）：675-690.

［7］LEU Y Y，MATHESON L A，REES L P.Sequencing mixedmodel assembly lines with genetic algorithms［J］.Computers&Industrial Engineering，1996，30（4）：1027-1036.

［8］MORADI H，ZANDIEH M，MAHDAVI I.Non-dominated ranked genetic algorithm for a multi-objective mixed-model assembly line sequencing problem［J］.International Journal of Production Research，2011，49（12）：3479-3499.

［9］DONG Qiaoying，KAN Shulin，GUI Yuankun，et al.Mixed model assembly line multi-objective sequencing based on modified discrete particle swarm optimization algorithm［J］.Journal of System Simulation，2009，21（22）：7103-7108（in Chinese）.［董巧英，阚树林，桂元坤，等.基于改进离散微粒群优化算法的混流装配线多目标排序［J］.系统仿真学报，2009，21（22）：7103-7108.］

［10］RAHIMI-VAHED A，MIRZAEI A H.A hybrid multi-objective shuffled frog-leaping algorithm for a mixed-model assembly line sequencing problem［J］.Computers &Industrial Engineering，2007，53（4）：642-666.

［11］WANG Guangbiao，YANG Shuying，FENG Fan，et al.Research of image classification based on cat swarm optimization［J］.Journal of Tianjin University of Technology，2012，27（5）：35-39（in Chinese）.［王光彪，杨淑莹，冯 帆，等.基于猫群算法的图像分类研究［J］.天津理工大学学报，2012，27（5）：35-39.］

［12］CHU S C，TSAI P W，PAN J S.Cat swarm optimization［J］.Lecture Notes in Computer Science，2006，4099：854-858.

［13］CHU S C，TSAI P W.Computational intelligence based on the behavior of cats［J］.International Journal of Innovative Computing，Information and Control，2007，3（1）：163-173.

［14］PRADHAN P M，PANDA G.Solving multiobjective problems using cat swarm optimization［J］.Expert Systems with Applications，2012，39（3）：2956-2964.

［15］OROUSKHANI M，MANSOURI M，TESHNEHLAB M.Average-inertia weighted cat swarm optimization［J］.Lecture Notes in Computer Science，2011，6728：321-328.

［16］TSAI P W，PAN J S，CHEN S M，et al.Parallel cat swarm optimization［M］.Washington，D.C.，USA：IEEE，2008：3328-3333.

［17］KALAISELVAN G，LAVANYA A，NATRAJAN V.Enhancing the performance of watermarking based on cat swarm optimization method［C］／／Proceedings of 2011International Conference on Recent Trends in Information Technology.Washington，D.C.，USA：IEEE，2011：1081-1086.

［18］LIN K C，CHIEN H Y.CSO-based feature selection and parameter optimization for support vector machine［M］.Washington，D.C.，USA：IEEE，2009：783-788.

［19］DEB K，AGRAWAL S，PRATAP A，et al.A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization：NSGA-II［J］.Lecture Notes in Computer Science，2000，1917：849-858.

［20］COELLO COELLO C A，LECHUGA M S.MOPSO：aproposal for multiple objective particle swarm optimization［M］.Washington，D.C.，USA：IEEE，2002：1051-1056.

［21］ZITZLER E，THIELE L.Multiobjective evolutionary algorithms：a comparative case study and the strength pareto approach［J］.IEEE Transactions on Evolutionary Computation，1999，3（4）：257-271.