X-C 直驱平台平面曲线轮廓磨削廓形误差非线性耦合控制

彭宝营，蔡力钢，韩秋实，杨庆东，李启光

（1.北京工业大学 机械工程与应用电子技术学院，北京 100022；2.北京信息科技大学 机电工程学院，北京 100192）

0 引言

平面曲线轮廓回转类零件（如凸轮、椭圆活塞、转子发动机燃烧室等）的磨削，普遍采用X，C 两轴联动加工，廓形精度要求很高。由永磁同步直线电机（PMLSM）及永磁环形力矩电机（PMRTM）组成的X-C 直驱磨削加工平台，会由于加工轨迹变化、负载扰动、机械延迟及两轴驱动系统参数不匹配等因素，引起X，C 轴跟踪误差，在很大程度上影响轮廓加工的精度［1-3］。研究表明，与先进的单轴伺服控制器相比，基于轮廓廓形误差的多轴耦合控制是提高系统轮廓精度更有效的途径［4］。

Yeh等［5］首先提出双轴耦合控制策略，然而该方法没有考虑刀具半径的存在使加工坐标误差不能等同于轮廓误差的问题，不能有效地适用于曲线轮廓加工廓形误差控制；Lo等［6］提出加工坐标转换的方法来减小轮廓误差，并设计了切向轮廓误差控制器（Tangential Contouring Controller，TCC），但其本质为恒增益的坐标转换补偿，所建立的轮廓误差无法适用于曲线轮廓补偿；Su等［7］在实时轮廓误差计算法则的基础上，提出了基于摩擦前馈的改进型X-Y 平台耦合控制方法，该方法适用于曲线的轮廓误差控制，但不能有效减小跟踪的位置误差，改善轮廓误差精度的效果并不理想。一些文献在X-Y 直驱平台的廓形误差补偿控制方面进行了研究，例如Slin等［8］设计了耦合鲁棒控制器用于多轴非线性运动控制系统的轮廓误差补偿控制。此外，一些研究人员采用等效误差［9］、重复跟踪控制［10］等先进的控制方法设计耦合控制器，以提高控制器的响应能力，这些方法计算过程复杂、响应速度慢，不适合数控系统使用。

上述研究都基于加工坐标轨迹偏差等同于轮廓廓形偏差的前提，在非圆轮廓切点跟踪磨削加工中，由于轮廓特征、砂轮半径等因素，加工坐标为砂轮中心轨迹，并不是真正的切触点，加工坐标误差并不直接等同于廓形误差。而且，研究内容大多集中于XY 平台的轮廓误差控制，X-C 平台耦合控制的相关研究较少。李静等［11］对X-C 平台的非圆轮廓耦合控制进行了研究，但采用的仍然是X-Y 平台廓形误差计算方法替代X-C 平台廓形误差计算。与X-Y平台不同的是，X-C 平台的单轴跟踪误差对廓形误差的形成不但存在耦合影响，而且各自对误差形成的影响不同，其廓形误差还与轮廓轨迹及砂轮半径等因素密切相关。

本文以X-C 直驱磨削平台平面曲线轮廓的廓形误差控制为研究对象，首先提出X-C 平台单轴跟踪误差耦合形成廓形误差的计算模型，设计了耦合非线性轮廓误差控制器，利用非线性控制器的快速自适应能力减小耦合轮廓误差。最后进行了仿真与实验验证，为平面曲线轮廓类零件X-C 加工质量的提升提供了依据。

1 X-C 直驱平台廓形误差分析

1.1 平面曲线轮廓X-C 加工原理

X-C 直驱加工平台由直线电机和力矩电机构成，加工对象一般为非圆回转类零件，刀具为砂轮。其中：X 轴由直线电机带动砂轮架水平往复移动，C轴由力矩电机带动工件旋转，X，C 轴两轴联动完成零件的加工。

平面曲线轮廓X-C 联动磨削的加工原理如图1所示，对于非圆轮廓极坐标方程ρ=ρ（φ），其廓形XC 联动加工公式为

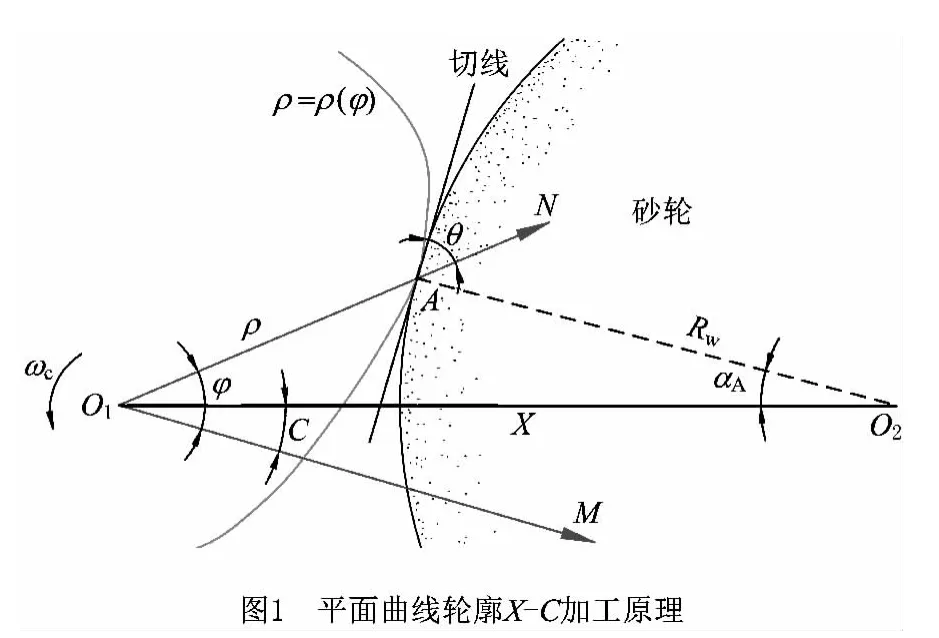
1.2 X-C 跟踪误差与廓形误差

X-C 单轴跟踪误差主要指伺服误差，即某一时刻电机指令位置与实际位置之差。因为X-C 直驱平台直接驱动工件及砂轮部件，减少了中间环节，所以控制补偿X-C 单轴跟踪误差，就能在很大程度上减小最终的加工廓形误差。

引起X-C 单轴跟踪误差的原因有很多，如磨削力的变化、加工速度的变化、机床振动等都会引起X，C 轴跟踪误差的变化；此外，系统动态的非线性、不确定性因素，如数控系统的死区、限幅及机床温度等，也会引起X，C 轴跟踪误差的变化。

平面曲线轮廓误差指实际位置与指令位置在轮廓轨迹指定点处法线方向上的偏差，用ε表示。由式（1）可知，X-C 直驱平台磨削非圆零件时，由X-C单轴跟踪误差并不能直接形成廓形误差，廓形误差还与砂轮半径、廓形轨迹等因素密切相关。

1.3 平面曲线轮廓轮廓X-C 廓形误差模型构建

根据图1可知，X-C 单轴跟踪误差沿法向O2A方向的误差分量的矢量和为最终的廓形误差。因此，分别对由X-C 单轴跟踪误差引起的廓形误差进行分析，将二者法向矢量进行叠加，即可得到最终的廓形误差。

X 轴跟踪误差引起的廓形误差分析如图2 所示。理论加工点为A 点，当X 轴跟踪误差为ΔX时，使实际加工点变为A1点，引起相应的廓形误差为εx。

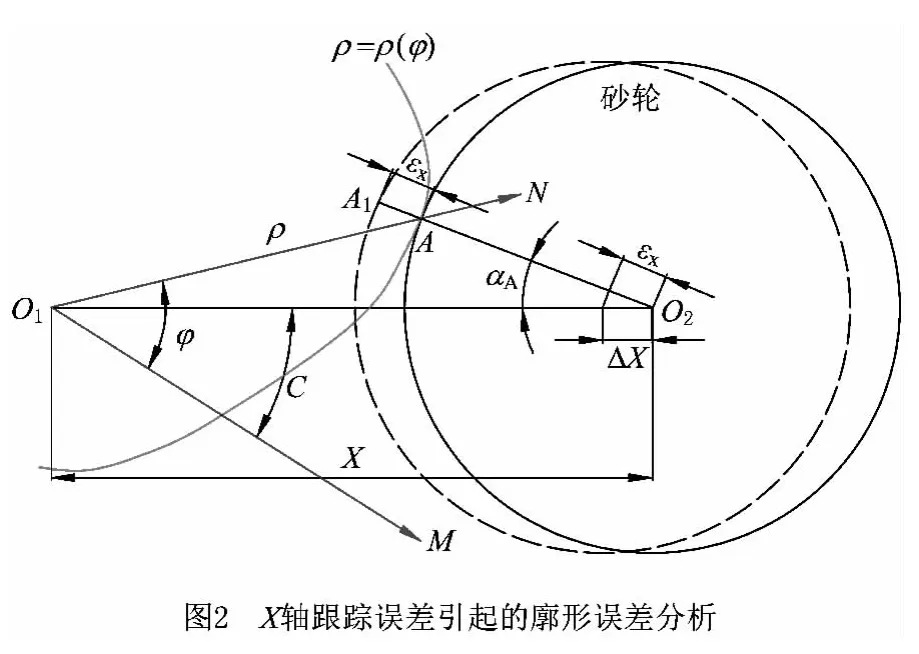
利用三角几何关系可以得到X 轴跟踪误差引起的廓形误差计算公式

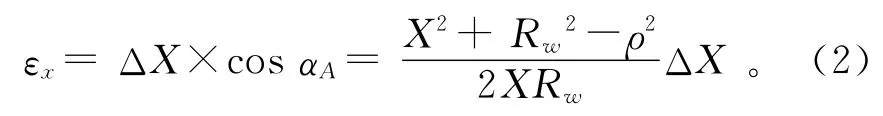
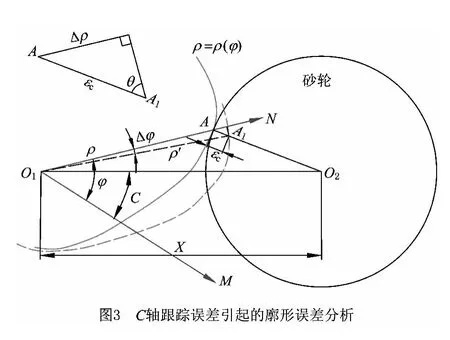
C 轴跟踪误差引起的廓形误差及局部放大图如图3所示。在极坐标系MO1N 中，理论加工点为A（ρ，φ）点，当C 轴跟踪误差为ΔC 时，实际加工点变为A1（ρ+Δρ，φ+Δφ）点，引起相应的廓形误差为εc。

利用三角几何关系可以得到C 轴跟踪误差引起的廓形误差

按泰勒展开，将ρ（φ+Δφ）≈ρ（φ）+ρ′（φ）Δφ 及代入式（3），得到C 轴跟踪误差引起的廓形误差

由式（1）可知，对于同一个理论点，ΔC=Δφ。将式（2）和式（4）联立，得到平面曲线轮廓X-C 联动加工廓形误差计算公式

2 X-C 直驱平台耦合控制器设计

2.1 X 轴单轴控制器设计［12］

对于直线电机采用d-q 坐标系下的模型，电流内环采用电流在d 轴上的分量id=0的控制策略，使定子电流矢量与永磁体磁场在空间正交。在理想情况下，其直轴、交轴的电压方程为

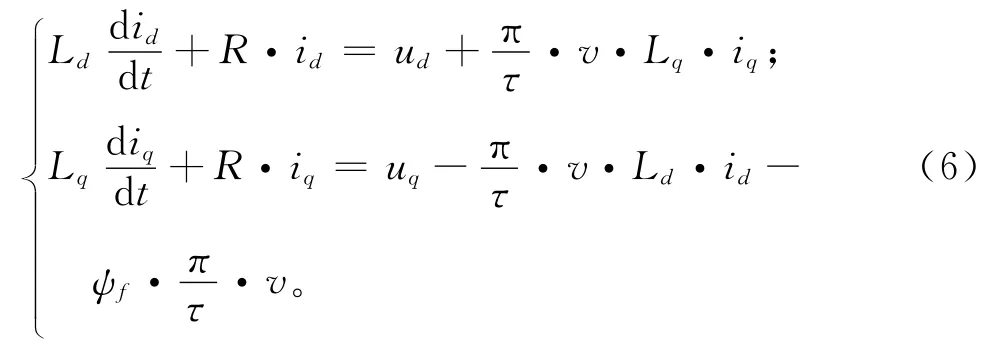
直线电机电磁推力及机械运动方程为

式中：Fe为电磁推力；τ为极距；f为频率；R为永磁同步直线电机的动子绕组电阻；Ld和Lq分别为永磁同步直线电机d 轴和q 轴电感；ud和uq为永磁同步直线电机电压的d 轴和q 轴分量；Fd为直线电机的负载；Ψf为永磁体磁链。

X 轴直线电机矢量控制仿真的程序框图如图4所示。

2.2 C轴单轴控制器设计［13］

忽略铁芯饱和、磁滞损耗、阻尼绕组等因素的影响，环形永磁力矩电机系统的数学模型为

式中：ud和uq分别为d 轴和q 轴上的定子电压；id和iq分别为d 轴和q 轴上的定子电流；Ld和Lq分别为d 轴和q 轴上的定子电感；Rs为定子绕组电阻；Ψf为永磁体磁链；p 为极对数。

C 轴力矩电机直接转矩控制仿真的程序框图如图5所示。

2.3 X-C 直驱平台耦合控制方案设计

在X-C 单轴控制的基础上，采用耦合控制［14］方法进行非圆面轮廓误差补偿控制，以减小廓形误差。X-C 直驱平台耦合控制原理图如图6所示，其控制思想是首先将X-C 的跟踪误差在耦合控制器中进行综合，计算得到廓形误差；然后经过非线性比例-积分-微分（Proportional-Integral-Derivative，PID）控制器进行调节，将误差信息分配给各轴以产生相应的实时附加补偿作用。设Gx 与Gc 分别为X 轴和C 轴耦合控制器的耦合增益，由式（5）可得

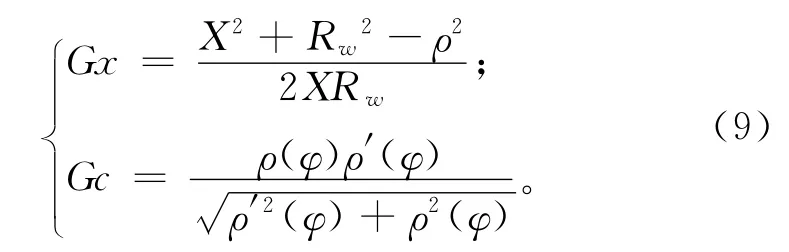
2.4 非线性耦合PID 控制器设计

非圆轮廓加工过程中存在大量的非线性环节，传统的定值PID 很难取得满意的控制效果。如果非线性PID 的各项参数选择适当，能够使控制系统响应快且无超调现象。另外，因为非线性PID 中的参数能够随控制误差变化，所以其抗干扰能力也大大超过常规线性PID 控制［15］。一般系统的阶跃响应如图7所示。

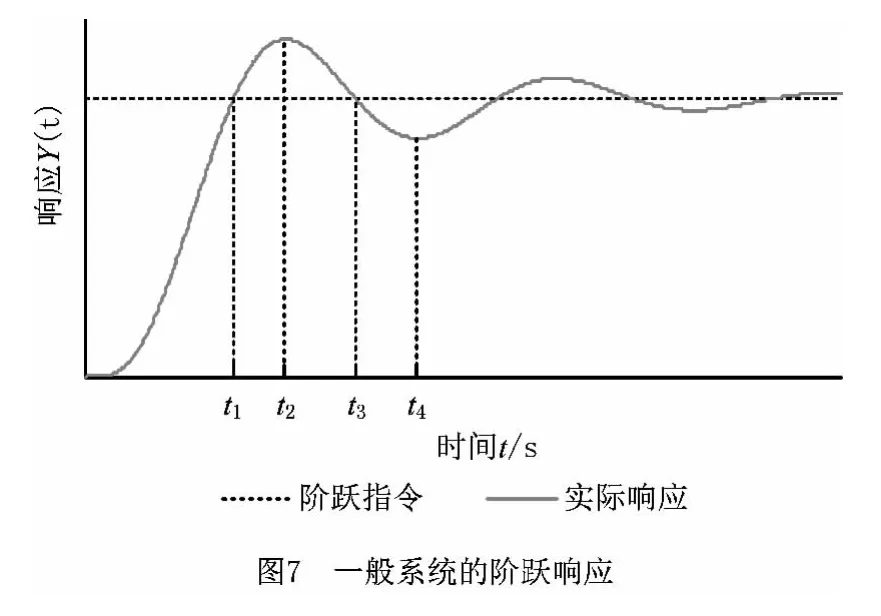
为减小控制误差抑制误差的变化趋势，在t1，t2，t3和t4时刻，比例Kp、积分Ki、微分Kd的变化过程如表1所示［16］。

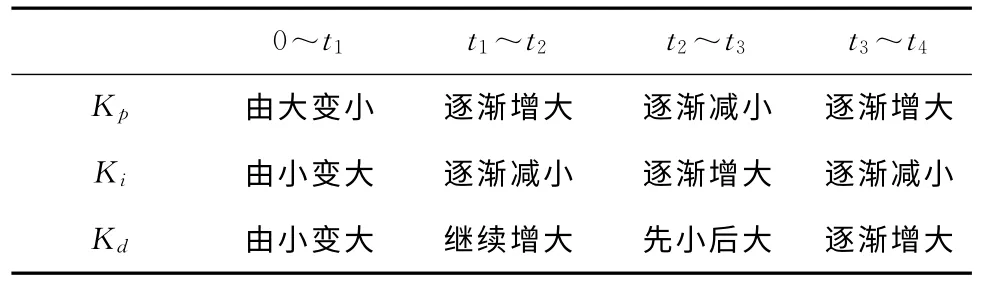
表1 非线性PID阶跃响应参数变化过程

非线性PID 在不同响应区域，比例、积分和微分分别取不同的值，其变化趋势可用双曲函数及e指数函数表示。Kp，Ki和Kd的连续时域计算公式为［17］

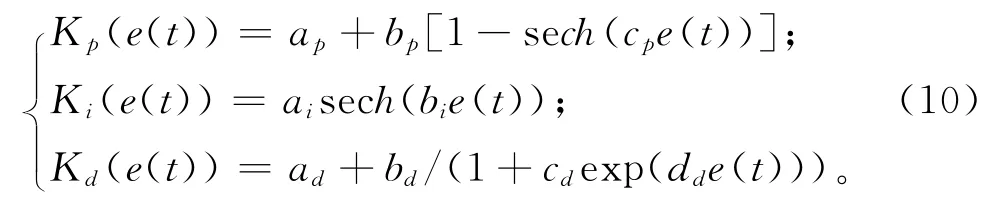
式中：ap，bp，cp，ai，bi，ad，bd，cd，dd均为正实数，通过调整cp，bi和dd的大小可以分别调整Kp，Ki和Kd的变化速率。

本文设计的廓形误差非线性耦合补偿控制器Simulink仿真程序图如图8所示，图中增加了前馈环节，以提高控制器的预测控制能力，比例、积分和微分三项参数按式（10）计算。

3 仿真实验及验证

凸轮是平面曲线轮廓X-C 联动加工零件的典型代表，以平底直动凸轮加工为例，建立了X-C 直驱平台仿真平台。采用砂轮反转法验证了平面曲线轮廓X-C 廓形误差计算模型的有效性，并对廓形误差的非线性耦合控制效果进行仿真验证。

3.1 X-C 直驱平台廓形误差控制仿真模型的建立

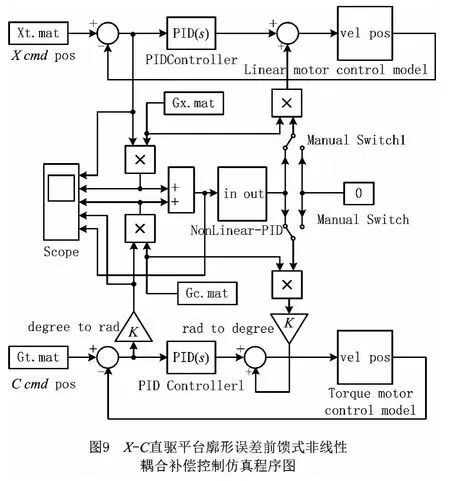
X-C 直驱平台廓形误差非线性耦合补偿控制Simulink仿真程序图如图9所示。其中，直线电机模型按图4所示的直线电机矢量控制Simulink仿真程序图建立；力矩电机模型按图5所示的力矩电机直接转矩控制Simulink仿真程序图建立；非线性廓形误差调节模块按图8所示的非线性耦合补偿控制Simulink仿真程序图建立。Xt，Ct为X-C 单轴指令位置；Gx，Gc为X 轴、C 轴的廓形误差增益。

3.2 凸轮廓基本参数

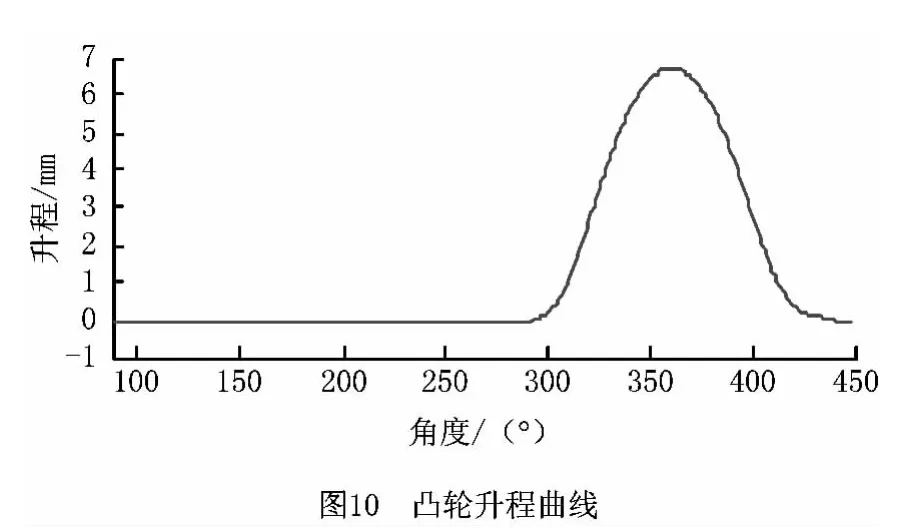
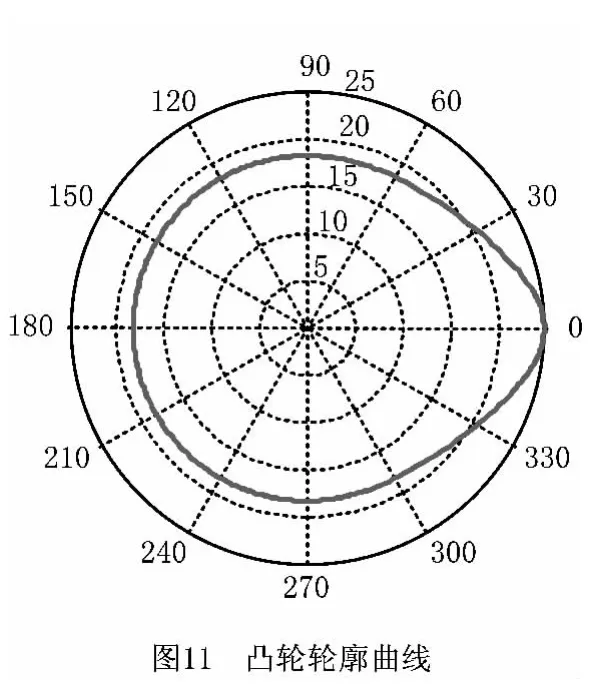
凸轮升程曲线如图10所示，极坐标廓形图如图11所示。

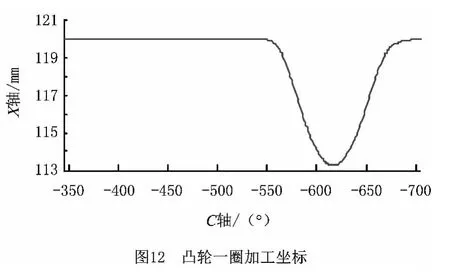
其中该凸轮一圈加工的X-C 坐标如图12所示。

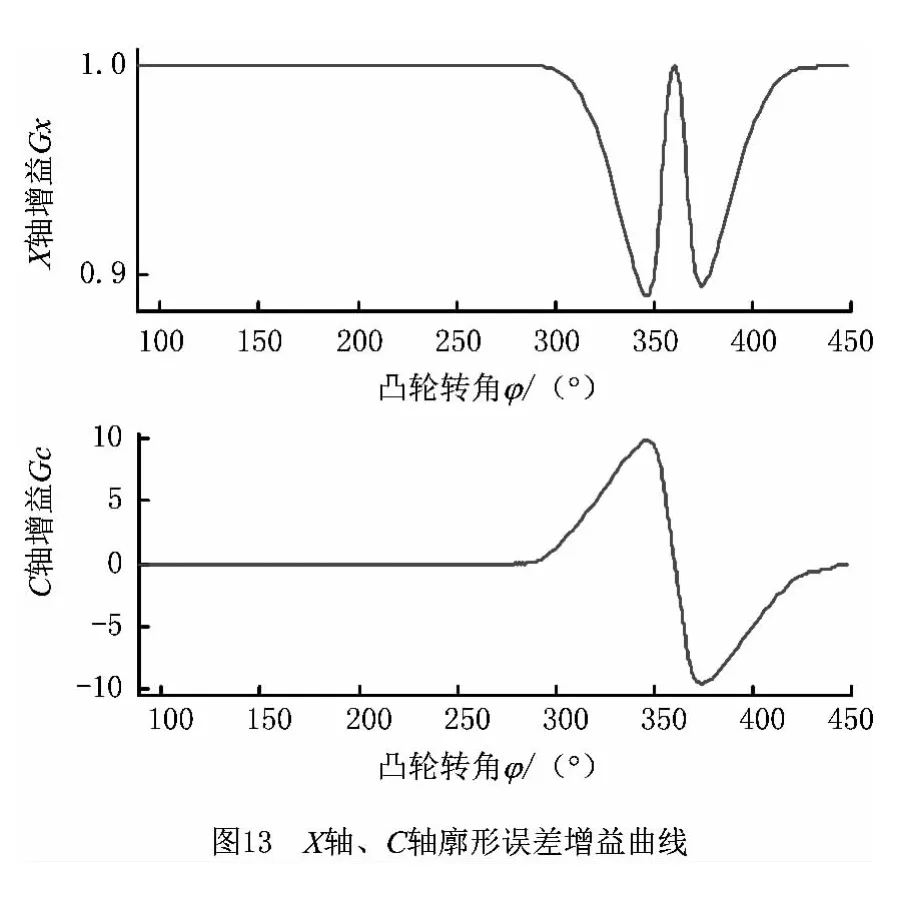
按照式（9）分别计算出X，C 轴廓形误差耦合增益Gx，Gc，如图13所示。

3.3 凸轮廓形误差非线性耦合控制仿真

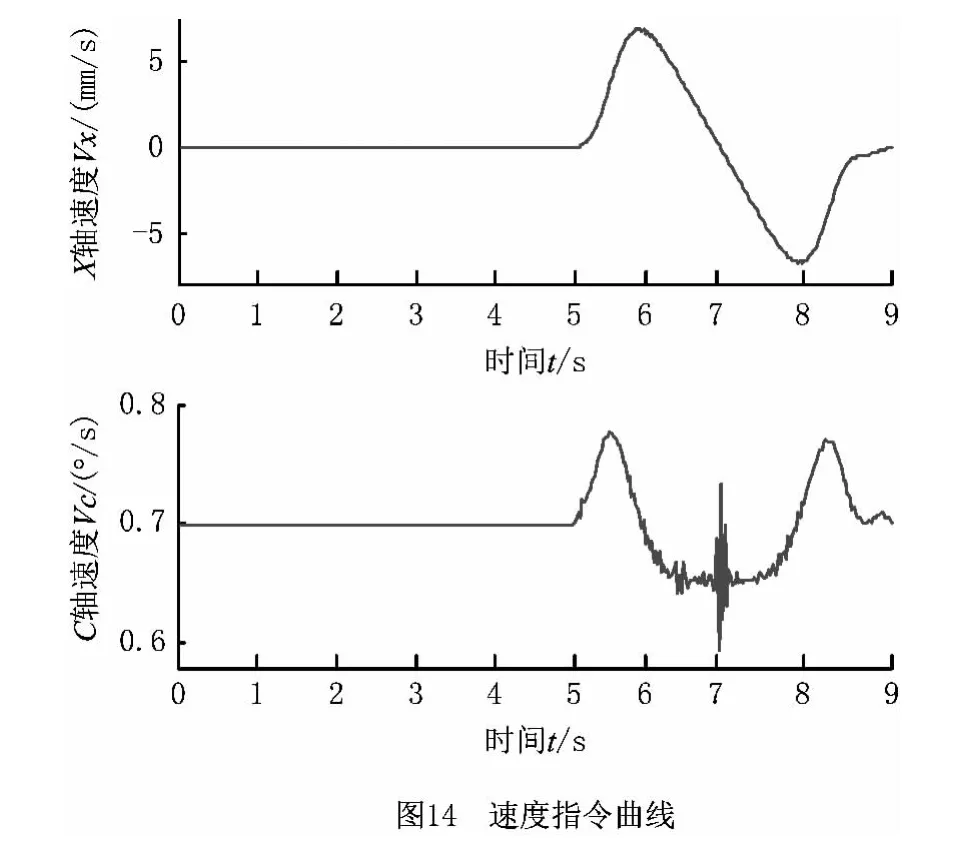
按图9所示的X-C 直驱平台廓形误差控制仿真模型，进行凸轮廓形误差非线性耦合控制的仿真实验。X-C 单轴位置指令按图11所示发出，凸轮一圈加工时间为9s，仿真结果采样周期设置为0.025 s。仿真过程中，X 轴的速度指令Vx 和C 的轴速度指令Vc 如图14所示。

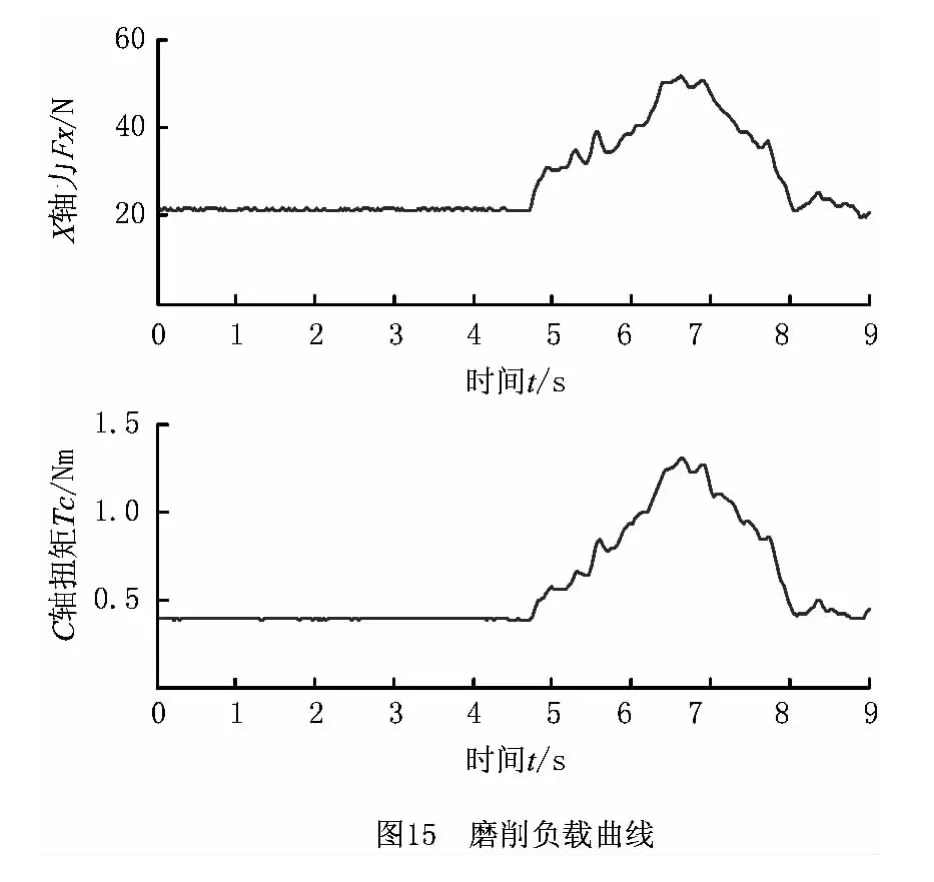
采用测力仪测量凸轮磨削过程中的一组磨削力并中值滤波后，按照凸轮表面的切线方向计算出X轴所受的磨削力和C 轴承受的扭矩，如图15所示。仿真过程中按图15所示的负载曲线，分别对X 轴的直线电机、C 轴的力矩电机施加模拟负载。

仿真过程中，X 轴、C 轴的PID 各项参数及非线性廓形误差控制器的各项初始控制参数如表2所示。

表2 廓形误差非线性耦合控制仿真参数

续表2

3.4 仿真结果分析

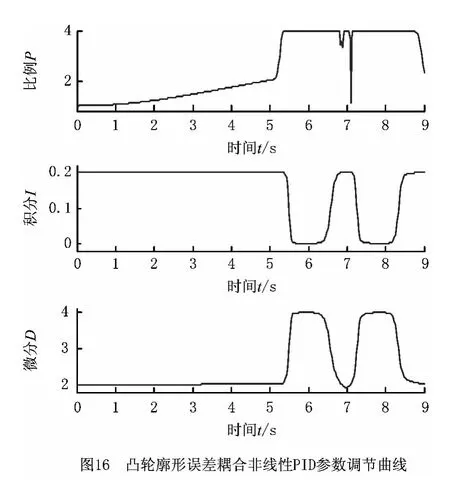
采集仿真过程中的非线性PID 参数调节曲线如图16所示。与图14和图15对比可以看出，在7 s左右，由于加工坐标转换导致的加工点间距不均，C 轴在该处速度波动较大，同时该处的磨削力较大，廓形误差非线性PID 迅速进行了调节。

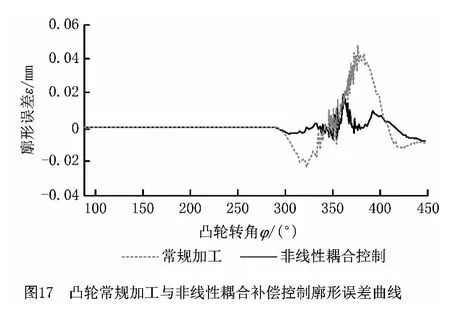
分别采集常规加工与采用非线性耦合控制仿真中的廓形误差，得到常规加工与采用非线性耦合补偿控制的结果廓形误差对比，如图17所示。可以看出，与常规加工相比，非线性耦合控制较廓形误差最大值下降了一半，而且更加均匀。

4 结束语

本文提出廓形误差计算模型，可用于平面曲线轮廓X-C 磨削加工中快速计算廓形误差并提供补偿系数。与常规控制相比，非线性耦合控制可以快速应对曲线加工过程的轮廓轨迹、磨削力变化、加工速度变化、控制系统死区以及限幅对廓形误差的影响，在一定程度上提高了X-C 直驱平台平面曲线轮廓零件的轮廓加工精度。

对于引起跟踪误差及廓形误差的其他因素，如机床振动、温升及加工过程中其他动态的非线性、不确定性因素的控制效果，有待于进一步研究。

［1］WANG Limei，WU Zhitao，SUN Yibiao，et al.Contour error analysis and normal cross-coupled control for direct drive XY table［J］.Electric Machines and Control，2006，14（9）：63-68（in Chinese）.［王丽梅，武志涛，孙宜标，等.直接驱动XY 平台轮廓误差分析及法向交叉耦合控制［J］.电机与控制学报，2006，14（9）：63-68.］

［2］SHEN Nanyan，HE Yongyi，WU Ganghu.Calculation model of the deformation due to grinding force in crank pin non-circular grinding［C］／／Proceedings of IEEE International Conference on Technology and Innovation.Washington，D.C.，USA：IEEE，2009：1325-1330.

［3］LI Jing，HE Yongyi，SHEN Nanyan，et al.Research on the servo lag error and compensation in cam non-circular grinding process［C］／／ Proceedings of International Conference on Measuring Technology and Mechatronics Automation.Washington，D.C.，USA：IEEE，2009：843-846.

［4］YEH S S，HSU P L.Analysis and Design of Integrated Control for Multi-Axis Motion Systems［C］／／Proceedings of IEEE International Conference on Control Systems Technology.Washington，D.C.，USA：IEEE，2003：375-382.

［5］YEH S S，HSU P L.A new approach to bi-axial cross-coupled control［C］／／Proceedings of IEEE International Conference on Control Applications.Washington，D.C.，USA：IEEE，2000：168-173.

［6］CHIU G T，TOMIZUKA M.Contouring control of machine tool feed drive system：a task coordinate frame approach［J］.Control system Technology，2001，9（1）：130-239.

［7］SU K H，CHENG M Y.Contouring accuracy improvement using cross-coupled control and position on error compensator［J］.International Journal of Machine Tools and Manufacture，2008，48（3）：1444-1453.

［8］SHIN Y T，CHEN C S，LEE A C.A novel cross-coupling control design for bi-axis motion［J］.International Journal of Machine Tools and Manufacture，2002，42（14）：1539-1548.

［9］WANG Limei，JIN Fuying，SUN Yibiao.Second order sliding mode control for linear motor XY table based on equivalent errors method［J］.Proceedings of the CSEE，2010，30（6）：88-92（in Chinese）.［王丽梅，金抚颖，孙宜标.基于等效误差法的直线电机XY 平台二阶滑模控制［J］.中国电机工程学报，2010，30（6）：88-92.］

［10］WANG Limei，LI Bing.Contour control for direct drive XY table based on real-time position compensation and repetitive control［J］.China Mechanical Engineering，2011，22（9）：1030-1034（in Chinese）.［王丽梅，李 兵.基于实时位置补偿交叉耦合控制与重复控制的直接驱动XY 平台系统设计［J］.中国机械工程，2011，22（9）：1030-1034.］

［11］LI Jing，HE Yongyi，FANG Minglun，et al.Cross-coupled contour control with variable parameters based on differential evolution algorithm in crankshaft non-circular grinding［J］.Journal of Mechanical Engineering，2011，47（9）：139-145（in Chinese）.［李 静，何永义，方明伦，等.曲轴非圆磨削中基于差分进化算法的变参数交叉耦合轮廓控制［J］.机械工程学报，2011，47（9）：139-145.］

［12］JIN Jianxun，ZHAO Huibin，XIN Ying，et al.Simulation and analysis of a PMLSM control system based on SVPWM Control［C］／／Proceedings of Control Conference.Washington，D.C.，USA：IEEE，2010：3316-3320.

［13］XIA Jiakuan，DONG Ting，WANG Chengyuan，et al.H∞robust controller design of direct drive ring PM motors used in NC rotary table［C］／／Proceedings of the 102Information Computing and Automation.Washington，D.C.，USA：IEEE，2007：1481-1485.

［14］KWON O S，CHOE S H，HEO H.A study on the dual-servo system using improved cross-coupling control method［C］／／Proceedings of the 2011 10th International Conference on Environment and Electrical Engineering.Washington，D.C.，USA：IEEE，2011：1-4.

［15］GUO Yanqing，YAO Zhuting，WANG Nan.The study on non-linear PID controller［J］.Journal of North University of China：Natural Science edition，2006，27（5）：424-425（in Chinese）.［郭彦青，姚竹亭，王 楠.非线性PID控制器研究［J］.中北大学学报：自然科学版，2006，27（5）：424-425.］

［16］SUN Wei，ZHOU Yanghua，XI Maolong.Method for parameter optimization of nonlinear PID controller［J］.Computer Engineering and Applications，2010，46（28）：246-248（in Chinese）.［孙 伟，周阳花，奚茂龙.非线性PID 控制器参数优化方法［J］.计算机工程与应用，2010，46（28）：246-248.］

［17］SERAJI H.A new class of nonlinear PID controllers with robotic applications［J］.Journal of Robotic Systems，1997，15（3）：161-181.