基于遗传算法的平均电流控制电路的优化设计

王志娟

(德州学院机电系，山东 德州 253023)

目前，开关电源向高频率、高效率、数字化、集成化方向发展，这是DC/DC 转换器的控制系统委员会提出的更高稳态和瞬态性能［1］。信号和大信号瞬态分析，DC/DC 开关稳压器系统的稳定分析及反馈控制电路的设计一直是电力电子领域有待解决的问题。加强这方面的研究，并结合高频开关电源的基本理论和实际应用对持续发展具有显著意义。本文在控制电路小信号模型的基础上，分析电流、电压控制环的主要作用，选择合适的适应度函数，利用改进的遗传算法对控制参数进行优化，并对优化结果进行了仿真分析。

1 控制电路结构及其基本工作原理

平均电流控制电路一般包括电压环和电流环两个控制环［2］。

电流环调节输入电流平均值，使其波形与输入电压波形相同。如图所示，经电压误差放大器放大后的输出电压，与全桥整流输出电压的采样在乘法器后作为基准电流送到电流运算放大器，作为基准控制输入电流平均值。

电压环通过控制电流基准、改变电感电流，来调节输出电压的稳定。PWM 调制器的误差放大器的输出电流直接控制电感电流的占空比，控制改变平均电感电流。当输出电压较高时，误差放大器的输出电压下降，使乘法器的输出参考电流下降，电感电流减小，来降低输出电压;反之，当输出电压较低时，误差放大器输出电压增加，使输出电压上升［2］。

2 控制参数的选择

有源功率因数调节器中有两个调变过程，一是输入端的桥式整流;二是乘法电路、除法电路与平方电路。每一个调变过程都会产生两个输入端间乘积、谐波或边频(Side Band)的影响。除此之外，这两个调变过程也会互相影响，相互解调。本文将在控制电路小信号模型的基础上，分析电流、电压控制环的主要作用，选择合适的适应度函数，利用改进的遗传算法对控制参数进行优化。

2.1 电流回路补偿网络参数的选择

内电流控制环路是通过调节电源电路的占空比，迫使输入电流跟踪获得的输入电压实现正弦波。由于输入电压是全波整流波形，包含丰富的谐波，因此为了更好地控制电感电流和得到良好的动态特性，要求电流控制环必须具有高频电流环路增益、高带宽和合理的相位裕度并有抑制开关噪声的能力。

电流环反馈补偿网络如图1 所示:

图1 电流环反馈补偿网络

则电流环的开环传递函数为［3］:

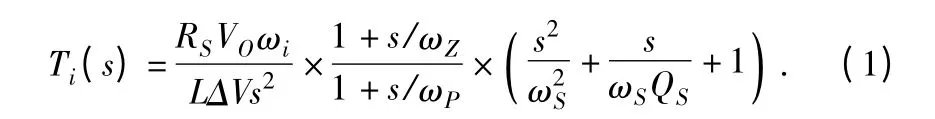
式中:RS为电流采样电阻，VO为输出电压，ωi=，L 为主电路电感，ΔV 为PWM 控制器三角波峰峰值，，ωS为切换频率ωS=。

设计变量:X=［x1，x2，x3，x4］=［RCI，CCP，RCZ，CCZ］，则求出电流环的开环传递函数与设计变量之间的关系式:

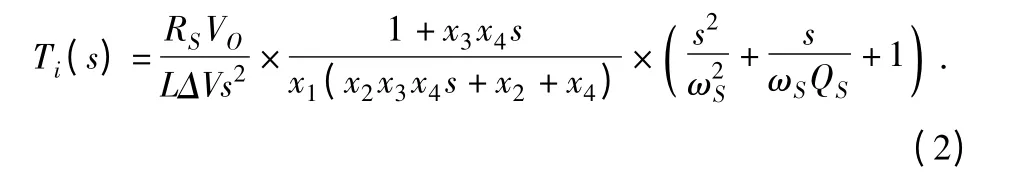
本设计中:

2.2 电压回路补偿网络参数的选择

为了使系统稳定，必须对电压控制回路进行补偿［4］。本设计中，电压环补偿网络如图2 所示。

图2 电压环反馈补偿网络

电压环的开环传递函数为:

选择设计变量:X=［x1，x2，x3］=［RVD，CVF，RVF］则:求出电压环的开环传递函数与设计变量之间的关系式为:

与电流环的优化过程相同，取与电流环优化过程相同的遗传操作变量，将系统在单位阶跃函数下的ITSE=J'=、电压环传递函数Tv(s)的纹波增益G2V结合，适应度函数取为其倒数:

式中:k1、k2分别为两个评价因子的权，本文均取为0.5。

3 遗传算法在控制参数选择中的优化设计

3.1 遗传算法的设计

遗传算法的一般过程可以分为初始化、选择、交叉和变异四个组成部分，其操作流程如图3 所示［5］。

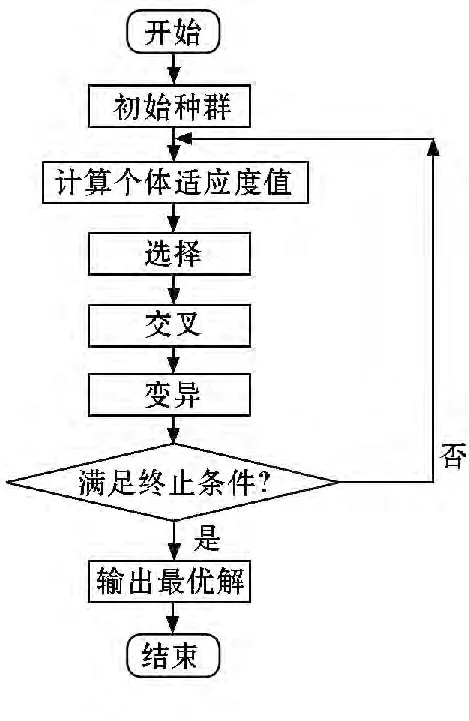
图3 遗传算法基本操作流程图

一轮遗传操作完成后，用每个新种群样本对应的一组寻优参数计算其适应度值，按从优到劣的次序排列，进行下一次迭代计算，直至达到满意的性能指标(或适应度值)。在最后的种群中，选择适应度值最大的一个样本，将其字符串解码，即得到最优的参数值。

3.2 遗传算法的改进(MGA)

在应用遗传算法优化的控制器参数时，应做到:

1)为克服二进制编码的不足，改用格雷码进行编码操作。

2)由随机数选择一个单独的适应度值比法有可能无法反映个体的适应正确，所以改用期望的方法来代替适应度值比法。

3)为提高优秀基因模式在一起的可能性，采用两个交叉操作。

在此基础上，进一步改进了算法如下:

1)更好地保护优秀个体

为保证全局收敛，防止优秀个体在交叉(变异)操作中被破坏，每一代种群中适应度值最大的个体直接进入下一代，不参加交叉和变异过程。

2)自适应变异策略

自适应温度的自适应策略应用于交叉和变异操作。定义T 为自适应温度:

式中:f 为某一代的平均值，fmax为最优个体适应度值。以T为依据设计遗传算子:

式中:a1，a2，a3，a4为恰当选择的常数，算子和自适应温度T呈简单的线性关系。

3)综合条件终止进化

判断算法是否终止进化的条件为:一，遗传代数达到固定的最大值;二，计算前后几代个体平均适应度的差(方差)小于设定的极小阈值。两个条件同时具备，就符合终止进化条件。

综合运用上述改进方法可提高算法的搜索效率，增强寻优能力，做到优势互补。

4 设计结果及分析

经过设计及优化设计，电流环和电压环的参数如表1 所示。

表1 补偿网络设计参数比较

电流环优化前后的特性指标如表2 所示。

表2 电流环特性指标对比

分别应用两组参数阶跃响应进行仿真，仿真结果比较如图4。

图4 两组参数阶跃响应的仿真比较

由图4 仿真结果及表2 的特性指标对比可知，优化后，电流环的增益裕量和相位裕量都得到了明显增加，稳定性也得到了很好地改善，开关噪声抑制能力有很大提高。

电压环优化前后的特性指标如表3 所示。

表3 电压环性能指标对比(误差带取5%)

分别应用两组参数进行仿真，其阶跃响应如图5 所示。

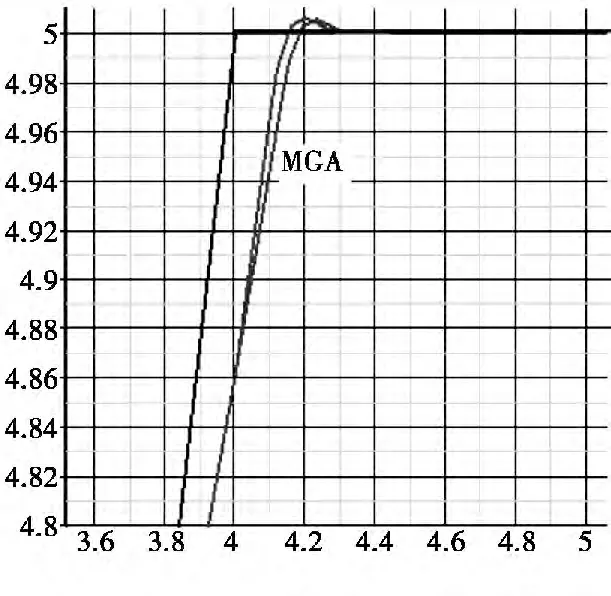
图5 两组参数阶跃响应的仿真比较

由图5 及表3 的特性指标对比可以明显看出，优化参数控制阶跃响应过冲减小，转换时间缩短，时域性能的控制系统大大提高。仿真结果表明了优化参数的有效性和优越性。

［1］张占松.高频开关变换技术教程［M］.北京：机械工程出版社，2010：13－20.

［2］Erickson R W，Maksimovic D.Fundamentals of Power Electronics.Second Edition［M］.Kluwer Academic Publishers，2001.

［3］朱小祥.高频电子技术［M］.北京：北京大学出版社，2012：56－59.

［4］林渭勋.现代电力电子技术［M］.北京：机械工程出版社，2006.

［5］关志华，寇纪淞，李敏强.一种改进的遗传算法Scatter GA［J］.控制与决策，2002，17(5) ：579－582.