浅谈数学课小组讨论的时机

文 路 云

新课程倡导“自主、合作、探究”的教学理念，而课堂教学中的“合作、交流”主要是通过“课堂讨论”来实现的。课堂讨论是合作学习与教师个别指导相结合的一种教学方式，因其具有使学生优势互补、形成良好人际关系、促进学生个性发展的优点，被越来越多的教师所采用。其实两千多年前的《学记》中就讲到学生之间可以“相观而善”的道理，认为“独学而无友,则孤陋而寡闻”。现代心理学也告诉我们：在解决简单问题时，独自面对比众说纷纭的效率高。但是面对复杂问题，群策群力却比孤军作战更有效，群体讨论产生的解决方案在数量和质量上都胜过个人。

因此在课堂教学改革的大背景下，课堂讨论便成为广大数学教师采用的一种新的教学形式，成为衡量一节数学课成功与否的一项重要参考指标。然而在实际教学中我们发现，很多教师一上课就出示问题，马上组织课堂讨论，然后请各小组学生代表发言。虽然这样表面上看起来很热闹，但由于时机把握得不够好，讨论氛围还没有形成，缺少思维的碰撞和交流，导致课堂讨论没有实际效果。为了充分发挥数学课堂讨论的整体功能，在教学设计和实践中，要把握好讨论的时机，选择好讨论的内容，使课堂讨论成为优化课堂教学的一种有效途径。下面笔者就针对讨论时机的把握谈谈看法。

一、讨论时机可选在“思维受阻”时

思路受阻是指学生对具体问题不能进行灵活、合理、抽象的加工，或不能以抽象规律为逻辑起点，经过逻辑中介，逐步演绎成具体，从而阻塞思维的情况。在教学过程中，由于受认知结构等智力因素的制约和诸多非智力因素的影响，学生对教师提出的问题往往不能够深刻理解，有时出现“卡壳”现象。遇到这种情况，教师应及时组织全体学生在出现思维受阻的问题上展开讨论，通过集体的智慧理顺思路，使思维受阻的学生茅塞顿开，明确知识掌握的薄弱点在哪里。讨论进行时，还应充分启发学生进行独立思考，鼓励他们各抒己见，引导他们逐步深入到问题的实质。

比如在全等三角形的复习课上遇到这样的问题：已知Rt△ABC中，∠C=90°，AC=BC=2，将一块三角尺的直角顶点与斜边AB的中点M重合，当三角尺绕着点M旋转时，两直角边始终保持分别与边BC、AC交于D、E两点(D、E不与B、A重合，如图1所示)。

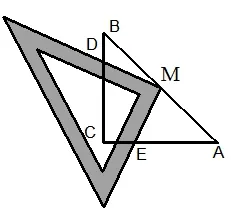
图1

(1)试说明：MD=ME；

(2)求四边形MDCE的面积。

很多学生开始都无从入手，这时教师可以适当点拨，说明两线段相等的常用方法是利用全等，而图中并没有现成的全等三角形，那么能否构造全等呢？然后让学生进行讨论交流，往往就能出现“柳暗花明”的境地。讨论就像一座桥，连接彼与此，它可以点燃学生思维的火花，启迪学生的智慧，引导学生掌握正确的思考方法，培养思维能力。

二、讨论时机可选在“意见分歧”时

由于学生思考问题的角度和认知水平不同，不同的学生对同一个问题会产生不同的想法，这是思维真实的表现。甚至有学生对某些内容产生理解偏差，没有进行取舍的判断力，觉得这种想法也对，那种方法也好。这时候教师不要轻易地将正确答案抛给学生，更不能简单地否定。而应充分发扬民主，从学生的想法中捕捉出有代表性的意见，引导学生讨论，鼓励学生畅所欲言，甚至展开争辩。然后有针对性地纠正错误，统一见解，从而激发学生的学习兴趣，唤起学生的求知欲。这样的效果比教师的“独白”会更好。

三、讨论时机可选在“解答开放”时

许多教师常说，现在的学生思维空间太狭窄，不灵活。其实，思维的活跃来源于开发。没有系统的训练，就不会有灵感的闪现。开放性问题就是很好的训练题材。要让学生围绕问题积极思考和讨论，让他们的思维发散出去，开拓他们的思维空间。在解决开放性问题时，学生的思维处于开放状态，不同的见解、不同的思路可以广泛地进行交流，并且能得到及时反馈，从而使学生的认识趋于完善。而且课堂讨论使部分较为内向的学生能逐渐适应讨论这种氛围，敢于谈论自己的想法，而不至于常常处于被动、消极地聆听和吸收的状态。部分外向学生也能够学会尊重别人的意见，在解决问题的过程中，逐渐学会谦虚和宽容。而对于少部分学习目的不明确的学生，则提供了一定的指向性，弥补了无向思维的空白。

数学中，常常会出现一些开放性问题。解答开放性问题的方法多种多样，而且结果也不唯一，不同学生常常发现不同的结果。正是这种差异的存在，为学生间的交流创设了良好的机会。教师应该抓住这样的机会，让学生在小组交流中自由地表述自己的观点和解题策略，倾听同伴的意见，并从中互相启发，互相补充，共同进步。

比如平行四边形复习时，要求学生研究平行四边形ABCD具有以下性质：(1)AB//CD；(2)BC//AD；(3)AB=CD；(4)BC=AD；(5)∠A=∠C；(6)∠B=∠D。若满足上述两个条件，能否保证四边形ABCD为平行四边形？此题有效地发挥学习的迁移作用，同时也为学生的创新学习搭桥铺路，以利于更好地激发他们的创新意识，培养创新能力。在教学过程中，首先让学生自己去慢慢感受开放题的特点，如有条件开放型、结论开放型、综合开放型、动手操作类开放探究性试题等，逐步体验做开放题的乐趣。然后小组讨论，说说自己的方法和理由。在多次体验的基础上，学生思维的灵活性、深刻性和发散性都得到了发展。而且在讨论中，学生不仅学会与他人交往和团队合作，在合作中享受知识的多样性和不确定性，对打开学生的思路也有很好的作用，而且可以极大地调动学生自主参与学习的积极性，使学生获得成就感，自然也就使学生在愉悦的心情下产生进一步探索和创造的愿望。

苏霍姆林斯基说：“人的内心有一种根深蒂固的需求。总感到自己是发现者、研究者。在儿童的精神世界中，这种需求特别强烈。”他们期望自己获得成功，期望感觉到自己智慧的力量，体验到创造的快乐。而这种快乐往往在小组讨论中得到极大的体现。“条条大道通罗马”，让学生讲述自己的解题方法，是给学生张扬个性、充分展示自己才华的机会。一展开讨论，不仅疑问豁然开朗，而且学生从他人的解题中获得了新思路，开阔了视野。

四、讨论时机可选在“生有疑惑”时

古人说：学起于思，思源于疑。没有疑惑，就引不起思考的兴趣，组织讨论的问题尤其是这样。学生在学习过程中，总会出现原有的认识结构与新知识的冲突，有的问题可以自己解决，但有的疑惑学生无法解决。在这种情况下，教师应鼓励学生多问，在此基础上组织学生交流讨论，帮助提问的学生解决问题。当学生在质疑问难过程中提出有探讨价值的问题时，教师要不失时机地组织讨论。

在教学《探索三角形全等的条件》时，当得出结论，直角三角形斜边和一条直角边对应相等时，这两个三角形全等，简称“斜边、直角边”。前面讨论过，如果直角变成锐角，这个结论是不成立的。这时候就有学生提出，那如果直角换成钝角呢？这时，笔者肯定了学生提出的问题，课堂上能大胆质疑，是主动精神的充分体现，敢问是一种良好的行为。然后让学生按小组展开讨论。经过讨论学生发现，当直角变成钝角时，依然全等。这时候让学生理解SSA就有了更深层次的体会。最后全班学生鼓掌感谢那位提出问题的学生，这位学生得到了鼓励，全班学生的认知也得到了提升。

通过小组讨论，使得学习困惑者在别人的帮助下，对原有的知识进行巩固，又沟通了新旧知识之间的联系，形成知识网络。同时，也培养了他们正确的信息迁移思维习惯。这样的讨论，由于学生间的双向信息是通过“学生语言”来交流的。因此，学生对讨论的内容更加容易理解和掌握，从而更顺利地完成知识建构。所以，当有思考价值的问题提出时，要把握好时机展开讨论，可以使学生大脑皮层高度兴奋，并使学生产生强烈的求知欲望。受这种欲望的驱动，学习过程往往会变得主动而富有生气。

五、讨论时机可选在“扩展深化”时

苏霍姆林斯基说：“教育的技巧并不在于能预见到课堂的所有细节，而在于能根据当时的具体情况，巧妙地在学生不知不觉中做出相应的变动。”课堂是充满生命灵性的，在动态的数学课堂中常会出现一些意外。这些意外往往是学生灵感的迸发、大胆的创意，是张扬学生个性、深化学生思维的契机。教师要善于捕捉这类意外，及时组织学生讨论，让学生的思维走向深入。

课堂教学要“抓纲靠本”，但这绝不意味着照本宣科。课本中的有些内容可以根据学生的接受能力予以扩展和深化，以启迪发展学生的思维。如在学习了整式乘法后，讨论（2+1）（2²+1）（2³+1）（24+1）…（216+1）+1的末尾数字是多少？如果教师直接讲的话，那么就是在这个式子前添加（2-1），然后利用乘法公式计算得到232，再利用规律21的末尾数字是2，22末尾数字是4，23末尾数字是8，24的末尾数字是6，25末尾数字是2……发现末尾数字4个一循环，从而得到本题的末尾数字为6。可是，学生讨论后却有另一种发现，即在几个因数中22+1=5，而5乘以一个整数，末尾数字要么是5，要么是0。这题中其余的几个因数都是2的N次方加1，都是奇数，则乘以5末尾一定是5，最后加1的话，末尾数字就是6了。发表这种意见的小组得到了全班学生的掌声。通过小组讨论既克服了思维定势，又拓展了思维。

叶圣陶先生主张：“教，是为了不教。”教师需要在引导学生掌握数学知识技能的同时，培养学生自主学习的能力，以及解决问题的能力。在教学中，尤其在练习拓展环节，抓住学生的思维亮点及时组织学生开展讨论，畅所欲言，往往能唤醒学生学习的主动性，将数学研究从有限的课堂延伸至更广阔的时空。

六、结束语

把握好课堂讨论的契机，充分发挥课堂讨论合作学习的作用，就能让学生以“学习的主人”身份积极思维。课堂讨论作为教学的一般方法，符合新课程标准的理念，它能为学生提供一个彼此沟通与交流的机会，能满足学生的自我表现欲，同时让不同层次的学生相互启发，有利于帮助学生养成表达和积极思考的习惯。它便于教师把握不同层次的学生的认知水平，从而调整教学策略，灵活施教，较好地完成教学任务，达到预期的教学目标。我们要让学生在讨论合作中学会学习，学会思考，学会表达，找到自信，共同提高，不断进步。