应用于天线座的并联机构构型设计*

□ 段艳宾 □ 贾彦辉 □ 李建军 □ 陆海坤

1.中国电子科技集团公司 第五十四研究所 石家庄 050081

2.河北远东通信系统工程有限公司 石家庄 050081

随着射电天文技术的发展，对射电天文望远镜天线的精度、速度等要求越来越高。由于传统方位俯仰天线座和XY型天线座存在如结构复杂、体积质量大、在天线连续转动时必须要有汇流环和关节、且存在跟踪盲区等缺点［1、2］，精度和速度越来越成为制约射电天文技术发展的主要因素，因此迫切需要在天线座架结构和控制上进行创新。在这些方面并联机构天线座有其自身的优点［3-5］，主要体现在：机械零部件主要由滚珠丝杠、虎克铰、球铰、伺服电机等标准通用元器件组成，其数目较串联机构大幅减少，因此结构简单，可靠性高；结构刚度大，承载能力强，静态误差小，刚度重量比远高于传统的方位俯仰天线座；各可伸缩杆杆长均能单独对动平台的位置和姿态起作用，不存在传统天线座的几何误差累积和放大的现象，甚至还有平均化效果，加之结构的对称性，故运动精度高；六杆天线座在天线连续转动时不需要汇流环和关节，且不存在跟踪盲区。

基于并联机构的种种优点，国内外学者开始研究将并联机构应用于天线座架［6］，以提高射电天文望远镜天线的运动速度和精度。

国内如华为实［7］研究了Stewart并联机构作为天线支撑的分析，邓先荣［8］在Stewart并联机构对雷达领域的应用进行了探讨，关贵注［9］等将并联机构应用于跟踪天线座进行了系统设计。但他们仅仅是将并联机构作为天线、雷达支撑的可行性进行了分析，并未对并联机构应用于天线支撑所存在的问题进行深入探讨。

笔者从实际设计角度出发，分析了影响Stewart并联机构作为天线座架的因素，提出了切实可行的设计方法，对并联机构应用于天线系统有重要参考意义。

1 构型设计影响因素

1.1 结构简介

如图1所示，Stewart并联机构由上下平台以及6条可伸缩支链组成，支链一端通过虎克铰与上平台连接，另一端通过球铰与下平台连接，影响其构型参数的主要有 R、r、H、θ1、φ1和 θ2、φ2。 其中 R 为固定平台上各铰点所在圆周半径；r为运动平台上各铰点所在圆周半径；H为动定平台铰点中心之间的距离；θ1、φ1为固定平台相邻两铰点间夹角；θ2、φ2为运动平台相邻两铰点间夹角。

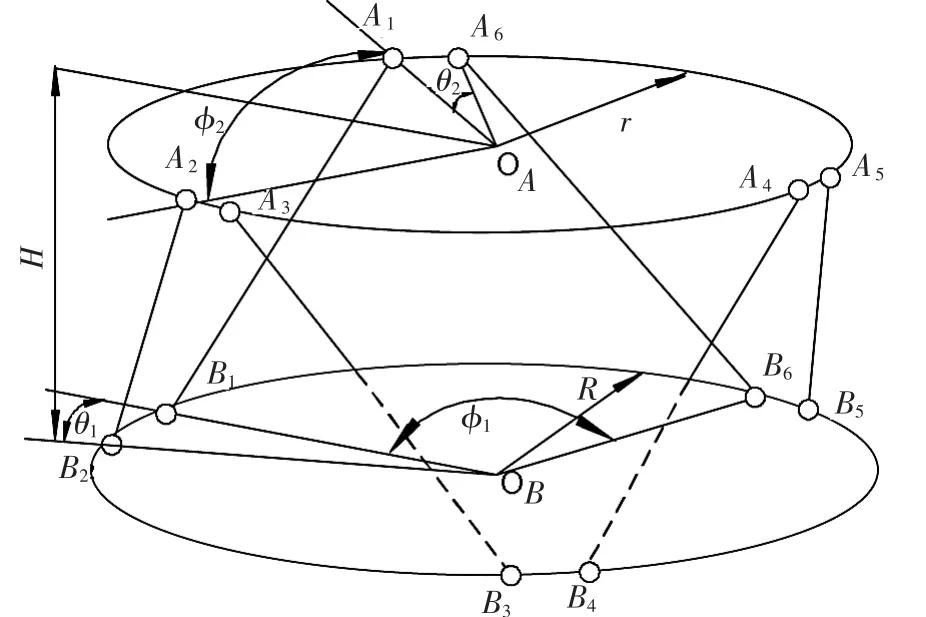
▲图1 Stewart并联机构结构示意图

1.2 影响Stewart并联机构功能工作空间的因素

1.2.1 杆长的限制

定义动平台的3个欧拉角为α、β、γ，则从动平台到定平台的姿态变化矩阵为：

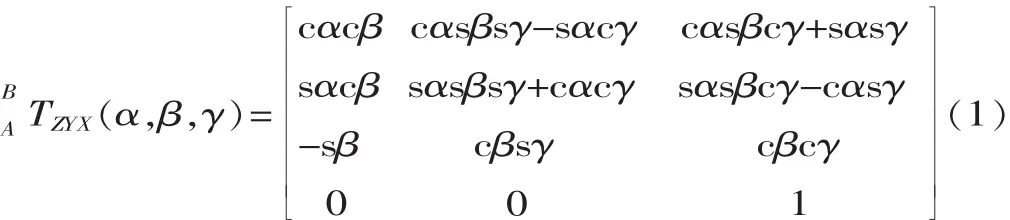
式中：cα=cosα，cβ＝cosβ，cγ=cosγ，sα=sinα，sβ＝sinβ，sγ=sinγ。

定平台上各虎克铰中心在定坐标系中的坐标为：

动平台上各球铰中心在动坐标系中的坐标为：

将动平台上各球铰中心在动坐标系中的坐标转化为在定坐标系中表示：

根据6个驱动杆的球铰中心点坐标和虎克铰中心点坐标，即可求得各驱动杆长度li：

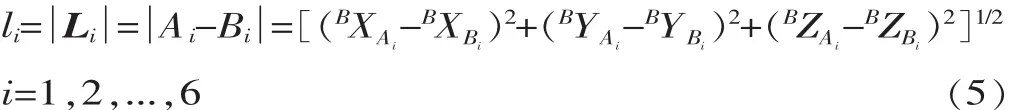
式中：li为各驱动杆长度。

式（5）为并联机构给定运动平台的位置和姿态后各分支杆所需要的杆长，但是杆长的长度变化范围是有限的，这里用lmin和lmax来表示第i个分支杆运动范围的最小值和最大值，则杆长的约束可以用，lmin≤li≤lmax表示，当某一杆长长度达到其极限时，运动平台上给定的参考点也就到达了工作空间的边界。

1.2.2 运动副转角的限制

机构上平台与各分支杆相连的关节为球面副，而下平台与各分支杆相连的关节是虎克铰，球面副和虎克铰的转角范围实际上是有限制的。

如图2所示，球面副的转角θ由球面副基座的坐标系Z轴和球面副的向量u确定，可以看出，球面副和虎克铰的最大转角θmax与运动副的具体结构有关。若第i个球面副的基座在坐标系｛A｝中的姿态用向量nAi来表示，则球面副的转角约束：

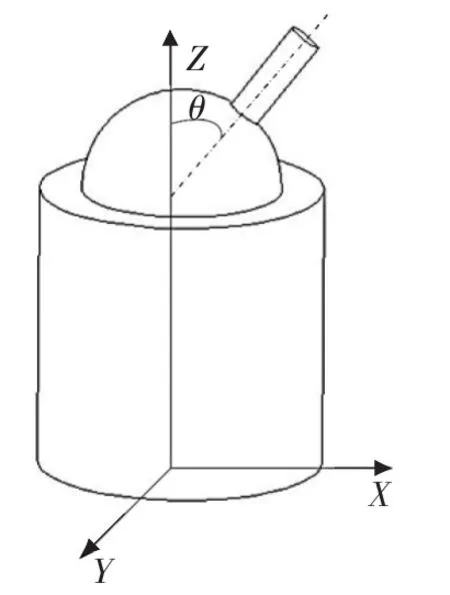
▲图2 球面副结构示意图

同样，虎克铰的转角约束：

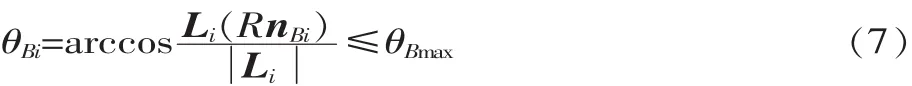
对于Stewart机构而言，影响其工作空间的主要因素为铰链的转动范围和杆长的限制，除此之外还有连杆之间的干涉、连杆与上平台之间的干涉等，这些需要在机械设计时加以注意。

2 构型优化

2.1 优化原则

由于六杆机构所涉及的参数较多，需要根据不同的应用场合制定合适的构型优化原则。

六杆机构应用于天线座，主要关心的是天线的方位、俯仰角度，天线需要方位360°旋转，俯仰角度为0～90°。因此六杆机构的优化原则首先是方位、俯仰角度都能到达指标要求。在指标达到要求的前提下，虎克铰、球铰所需的转动范围越小越好，且分支杆行程合适，在此基础上，分支杆的受力越小越好。故提出以下优化原则。

（1）方位、俯仰范围分别为 0～360°和 0～90°。

（2）在机构工作空间内，虎克铰、球铰运动范围在铰链设计范围之内。

（3）分支杆所需行程在安装范围内。

（4）在全工作空间内，分支杆所受力较小。

2.2 天线方位俯仰转角与铰链摆角及杆长关系

在转动方面，六杆机构有其独特的优势，如图3所示，图中，OA为动平台中心，OB为定平台中心，天线转动中心可以任意指定，即天线可以绕OA转动，也可以绕OAOB之间的任意点转动，如图3所示的O点。

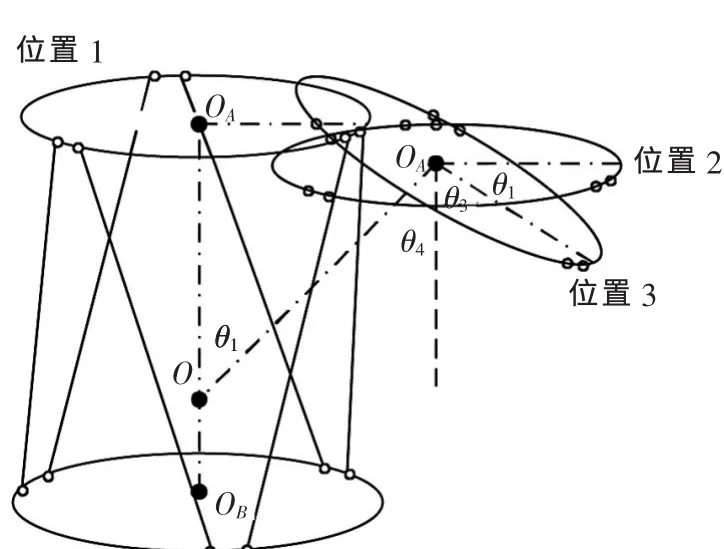
▲图3 运动平台转动示意图

从图3可得出，动平台绕O转动θ1可以看作动平台先从位置1平移到位置2，再绕OA转动θ1，也就是说动平台绕O转动θ1时，与动平台直接绕OA转动θ1指向一致，只是动平台中心点OA发生了变化。

因此，在俯仰控制时，控制思路为：上平台先绕中心点O转动θ1，再绕动平台中心点OA转动到90°。

根据以上分析，当机构构型确定后，影响机构转动能力的因素主要为虎克铰、球铰转动范围以及杆长行程。三者主要与以下两个参数有关。

（1）转动中心位置O。

（2）绕转动中心O转动角度θ1。

给定 R=725 mm、r=450 mm、H=2 900 mm，θ1=θ2=20°、φ1=φ2=100°。

根据结构构型以及杆长和铰链公式，按照上述控制思路，编程求取机构在全工作空间内运动过程中杆长最大行程及铰链的转动角度。

图4～图6中，横坐标为转动中心O距动平台距离，即OOA值；纵坐标分别为分支杆行程、铰链摆角等；不同直线表示不同θ1时分支杆行程、铰链摆角与OOA关系。

从图4中可以看出，当θ1一定时，分支最大行程随OOA增大而增大；从图5中可以看出，当θ1一定时，球铰所需最大摆角随OOA增大而减小；从图6中可以看出，当θ1一定时，虎克铰所需最大摆角随OOA增大而增大。θ1的值只是影响直线的斜率。

从图5中可以看出，在OOA和θ1均为0时，球铰最大摆角最大，已超过90°，而与之对应的虎克铰最大摆角较小，一般情况下，所设计的铰链最大摆角不超过90°，因此需要选择合适的OOA和θ1，使铰链最大摆角在所设计的范围内。

从图4、图5可知，OOA的值选择在H（动定平台之间距离）一半左右比较合适，因为此时分支杆行程增加较小，而所需球铰最大摆角下降较大。

▲图4 分支杆行程与转动中心及转动角度关系

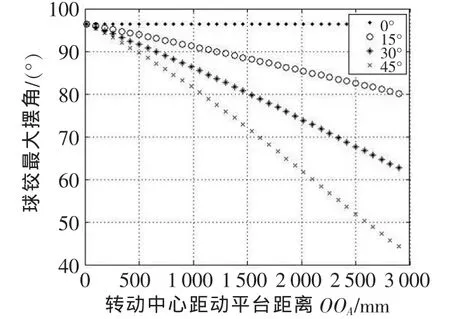
▲图5 球铰最大摆角与转动中心及转动角度关系

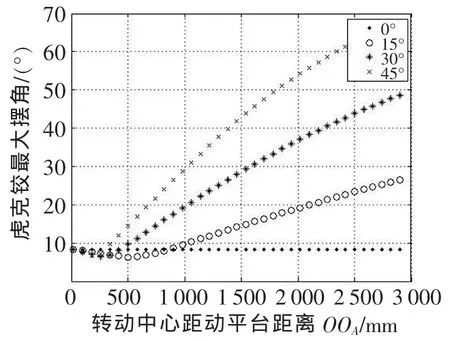
▲图6 虎克铰最大摆角与转动中心及转动角度关系

▲图7 优化过程流程图

综合分析，暂定OOA=0.5H、θ1=30°进行Stewart并联机构的结构优化设计。优化流程图如图7所示。

约束条件包括分支杆行程及安装空间、铰链摆角＜85°、铰链安装空间等。搜索范围为：R=300 mm～700 mm，r=200 mm～400 mm，H=1 200 mm～2 500 mm，铰链夹角范围 4～20°。

经编程计算，得到合适的构型，见表1。

表1 优化所得机构参数表

根据表1中的参数，利用MATLAB编程计算机构在负载5 000 N、方位 360°、俯仰90°工作空间内运动以及末端速度 10°/s、加速度 20°/s2时，分支杆上铰链转动范围、分支杆运动范围、受力及速度加速度情况见表2。

从表2可以看出，所设计的机构铰链运动范围、分支杆运动范围及分支杆速度、加速度、受力等均在可承受的合理范围内，说明通过以上优化算法能够优化出符合要求的并联机构天线座架。

表2 运动过程中分支杆参数表

3 结论

本文以应用于天线座架的Stewart并联机构为对象，研究了影响应用于天线座架的Stewart并联机构的构型的主要因素，建立了构型的优化原则，得到了并联天线座架方位俯仰转角与机构铰链摆角及杆长的关系，最后通过计算实例验证了构型优化原则的正确性。本文紧密结合实际要求，研究内容对于Stewart并联机构，真正应用于天线座架具有重要的理论指导意义。

［1］ 张燕.过顶跟踪的天线座设计方法 ［J］.无线电工程，1997，27（4）:37-39.

［2］ 吴风高.天线座结构设计［M］.西安：西北电汛工程学院出版社，1975.

［3］ Stewart D.A Platform with 6-DOF ［C］.Proceeding of the Institution of Mechanical Engineering，London，1965.

［4］ 黄真,赵永生，赵铁石.高等空间机构学［M］.北京：高等教育出版社,2005.

［5］ 韩秀英，刘延斌，贾现召.6-SPS型并联机构的混合坐标动力学建模［J］.机械设计与制造，2008（1）:4-5.

［6］ 华为实.基于3—RSR并联机器人机构的天线支撑 ［J］.机械，2000，27（5）:10-14.

［7］ 华为实.Stewart机器人用作天线支撑的分析 ［J］.电子科技大学学报，1999，28（4）:443-446.

［8］ 邓先荣.Stewart平台机构在雷达领域中的应用探讨［J］.电子机械工程，2009,25（2）：41-43.

［9］ 关贵注，李凉海，张雪峰，等.六自由度自跟踪天线座的系统设计［J］.遥测遥控，2007,28（11）：209-211.