重型卡车轮毂轴承中滚子的对数曲线凸度优化设计

□ 冯浩原 □ 剡昌锋 □ 吴旭东 □ 李志新

1.兰州理工大学 机电工程学院 兰州 730050

2.中核兰铀公司 兰州 730000

1 概述

轴承是装备制造业的关键基础件，圆锥滚子轴承在滚动轴承中使用数量仅次于深沟球轴承［1］。因为直母线的滚子轴承在受载后滚动体两端不可避免地存在边界应力集中现象，即所谓的“边缘效应”［2］，所以需要引入凸度设计来克服“边缘效应”［3］。

圆锥滚子轴承33022是常用的重型卡车轴承，它的寿命直接影响着整车的使用寿命。由于该轴承所受载荷较大，工况条件较差，轴承工作表面的边缘应力集中更加明显，所以通过优化滚子凸度，以此来减小应力集中现象，从而提高轴承使用寿命。

轴承凸度设计工作包括凸型的选择和凸度量的设计两个方面。Lundberg G［4］于1939年提出了著名的Lundberg凸型公式，该种凸型的加工难度和成本较高。Schauder B建立了圆柱滚子最佳凸型的数值计算方法，该方法将表面接触应力分解为作用于许多节点的相应集中力，并利用Boussinesq J半空间体力变形关系，计算滚子与内外圈接触区域的应力分布和表面变形情况。Hartnett M J提出了将结构分析中的影响系数法与Boussinesq J半空间体力变形关系结合起来的方法，可以求解一般表面轮廓的接触问题。本文采用Hiroki Fujiwara、Tatsuo Kawase提出的对数曲线凸型公式，利用有限元方法计算不同凸度量圆锥滚子的接触应力，以最小接触应力对应的凸度量为最优值，得到33022圆锥滚子的最佳凸度。

2 凸度的设计方法

目前在行业上普遍认同的凸型曲线有3种：全凸型、部分凸型（即圆柱修正线型）和对数曲线凸型。对数曲线凸型设计在减小接触应力带来的边缘效应上有显著效果，早期的对数曲线凸型公式是由Lundberg提出的，以凸度量 T（x）来衡量［5］：

式（1）存在着两个端点不连续的缺点，因此，Johns和Gohar又对Lundberg的对数曲线凸型进行了修正［6］：

式中：E′为等效杨氏模量；Q为载荷；a为1/2有效接触长度；b为1/2接触宽度。

在 Johns-Gohar的基础上，Hiroki Fujiwara、Tatsuo Kawase将公式进行了优化，引入了3个参数，如式（3）所示［7］：

式中：k1为综合载荷；k2为凸度长度与a的比值；Zm为曲线端点处对应的凸度量。

式（3）避免了由于滚子不对中引起的边缘应力，同时可以将内滚道与滚子接触区域设计成直线，方便设计计算和加工。

3 滚道与滚子的接触模型建立

3.1 二维模型建立

根据33022圆锥滚子轴承具体尺寸，采用内外滚道为直线和滚子为对数曲线凸型的凸度设计方案。通过有限元软件对滚子进行样条曲线拟合，对内外滚道进行直线拟合，由线生成面，得到几何模型。因为内外滚道都是固定状态，可将内外滚道与滚子接触区域视为无限半平面，滚子受力最大位置位于中心线处，为了节约计算时间，采用了二维模型进行计算，能够得到较为近似的结果。

3.2 有限元网格的划分及材料属性

由于不同的分析对象和分析类型对应不同的单元类型，所以选择合适的单元及网格尺寸来快速准确地计算出求解结果。在接触区域进行网格细化，内外滚道与滚子接触的接触应力采用增广拉格朗日方法进行计算，得到有限元网格模型，如图1所示。

33022轴承的内外圈和滚子都采用GCrl5材料，杨氏弹性模量E=206 GPa，泊松比γ=0.25。

▲图1 滚子和滚道有限元模型图

3.3 载荷施加

3.3.1 确定载荷

轴承受到的最大径向载荷为：

式中：Fr=0.2Cr，Cr为额定动载荷300 kN；Z为滚子数，Z=19；α 为偏心角，α=9.9°。

将数值代入式（4），求得Qmax=12.9 kN。

内滚道外圈受到的压强p为：

式中：l为内滚道长度，l=34 mm；b为内滚道有效接触宽度，b=2 mm。

将数值代入式（5），求得p=189 MPa

3.3.2 定义边界条件

对外滚道外圈分别在X、Y方向施加零约束，外滚道侧边、内滚道侧边、滚子侧边在X方向施加零约束，对内滚道内圈施加一个向外的压强p=189 MPa。

3.4 接触应力求解及优化

采用式（3）进行凸度设计，3 个参数 k1、k2、Zm分别取值为 k1=1、1.5、2、2.5、3，k2=0.1、0.2、 …、1，Zm=0.000、0.002、…、0.020mm。通过研究发现，只有当k2=0.5时，曲线是中心为0、两边对称的对数曲线，在其余取值下，曲线均不是两边对称的对数曲线，即确定参数k2=0.5，再确定Zm。接下来研究k1变化对接触应力的影响趋势，再根据k1、k2，研究Zm变化对接触应力的影响趋势。

求解后，提取内外滚道与滚子接触位置的接触应力。由于内滚道与滚子接触应力远大于外滚道与滚子的接触应力，故应着重分析内滚道接触区域接触应力的变化情况。

确定k1最优解时，在确定k2和Zm的情况下，先得到k1最优解范围，从而进一步优化，得出k1最优解的具体值。 取 k1=1、1.5、2、2.5、3，得到内滚道与滚子接触区域接触应力变化趋势，如图2所示。当k1=1时，最大接触应力pmax=1 943.8 MPa；k1=1.5时，最大接触应力pmax=2 387.1 MPa；k1=2时，最大接触应力pmax=2 425.4 MPa；k1=2.5 时， 最大接触应力 pmax=2 719.3 MPa；k1=3时，最大接触应力pmax=2 930 MPa。通过图2可以得出，当k1=1～1.5时，最大接触应力较小。通过二分法，取k1=1.3进行分析，接触应力变化趋势如图3所示。通过图3得出：当k1=1～1.3时，最大接触应力较小；k1=1.3时，最大接触应力pmax=2 268 MPa。再取k1=1.1、1.2进行分析，接触应力变化趋势如图4所示,得出：当k1=1.1时，最大接触应力pmax=1 841.4 MPa；k1=1.2时，最大接触应力pmax=1 752.9 MPa，该接触应力最小。

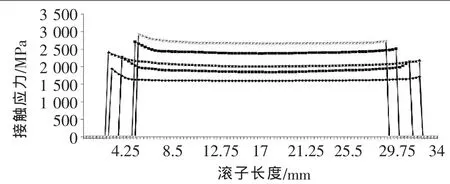
▲图2 k1=1、1.5、2、2.5、3 的接触应力值曲线（由上到下依次为 3、2.5、2、1.5、1）

▲图3 k1=1、1.3、1.5的接触应力值曲线（由上到下依次为 1.5、1.3、1）

▲图4 k1=1、1.1、1.2、1.3 的接触应力值曲线（由上到下依次为 1.3、1、1.1、1.2）

▲图5 Zm=0.000～0.006 mm的接触应力值曲线（由上到下依次为 0.000、0.002、0.004、0.006）

▲图6 Zm=0.008～0.014 mm的接触应力值曲线（由上到下依次为 0.014、0.012、0.010、0.008）

▲图7 Zm=0.016～0.020 mm的接触应力值曲线（由上到下依次为 0.020、0.018、0.016）

▲图8 Zm=0.006～0.008 mm的接触应力值曲线（由上到下依次为 0.008、0.006、0.007）

▲图9 不同k1下最大接触应力变化趋势

▲图10 不同Zm下最大接触应力变化趋势

确定k1后，改变Zm取值，间隔为0.002 mm，分别得出Zm=0.000、0.002、…0.020 mm时内滚道与滚子接触区域接触应力变化趋势，如图5、6、7所示。当Zm=0.000 mm时，最大接触应力 pmax=2 661.9 MPa；Zm=0.002 mm时，最大接触应力 pmax=2 247.5 MPa；Zm=0.004 mm时，最大接触应力 pmax=1 986.4 MPa；Zm=0.006 mm时，最大接触应力 pmax=1 752.9 MPa；Zm=0.008 mm时，最大接触应力pmax=1 920.7 MPa；Zm=0.010 mm时，最大接触应力 pmax=2 043.8 MPa，Zm=0.012 mm时，最大接触应力 pmax=2 256.7 MPa；Zm=0.014 mm时，最大接触应力 pmax=2 379.6 MPa；Zm=0.016 mm时，最大接触应力 pmax=2 521.3 MPa；Zm=0.018 mm时，最大接触应力 pmax=2 694.3 MPa；Zm=0.020 mm时，最大接触应力pmax=2 947.7 MPa，综合得出：当Zm=0.006～0.008 mm时，最大接触应力较小，取Zm=0.007 mm进一步分析，得到其接触应力变化趋势，如图8所示。观察得出：当Zm=0.007 mm时，最大接触应力pmax=1 507.3 MPa。通过图2、3、4可以得到k1变化对最大接触应力影响变化趋势，如图9所示。通过图5、6、7、8可以得到Zm变化对最大接触应力影响变化趋势，如图10所示。对于圆锥滚子，无凸度量或凸度量太大，均会导致明显的应力集中现象，当Zm=0.007 mm时，最大接触应力最小。即当k1=1.2、k2=0.5、Zm=0.007 mm时，内滚道受到的最大接触应力最小，为最佳凸度设计。

4 结论

本文以33022轴承滚子为实例，在额定载荷300 kN下，利用Hiroki Fujiwara、Tatsuo Kawase提出的对数曲线凸型进行凸度设计，引入 3个参数 k1、k2、Zm，对不同参数下的滚子凸度母线坐标进行计算，由坐标生成二维模型。通过有限元法计算不同凸度的圆锥滚子轴承对应的接触应力，分析结果表明，当k1=1.2、k2=0.5、Zm=0.007 mm时，最大接触应力最小，以最大接触应力值最小的凸度为优化原则，得到了一种基于有限元方法的圆锥滚子凸度量优化设计方法，该方法可快速、直观地对轴承凸度进行优化。

［1］ 刘恩时.中国轴承工业转变发展方式的思考［A］.2010上海国际轴承峰会演讲文集（一）［C］.上海：中国轴承工业协会，2010.

［2］ 施宝丽,赵淑丽,刘文波.边缘应力对轴承寿命的影响及凸度工艺［J］.汽车工艺与材料,2004（8）:20-23.

［3］ 吴飞科.圆锥滚子轴承接触应力分析及凸度设计 ［D］.洛阳：河南科技大学，2007：3-4.

［4］ Lundberg G.Elastic Contact between Semi-infinite Bodies［J］.Fur Schung Auf Dem Gebieto Des Engenienswesens，1961，10 （5）：165-174.

［5］ Tensner H.The Logarithmic Roller Profile-The Key to Superior Performance of Cylindrical and Taper Roller Bearing［J］.Ball Bearing Journal，1987，230：2-10.

［6］ P M Johns， R Gohar.Roller Bearings under Radial and Ecce-ntric Loads ［J］.Tribology International，1981，14（3）：131-136.

［7］ Hiroki Fujiwara，Tatsuo Kawase.Logarithmic Profiles of Rollers in Roller Bearings and Optimization of the Profiles ［J］.NTN Technical Review，2007（75）：140-148.