轮式移动机器人车轮牵引性能离散元仿真*
□ 刘吉成 □ 李 斌 □ 华凌云 □ 江盼阁
上海大学 机电工程与自动化学院 上海 200072
轮式移动机器人在松软的路面运动时,车轮极易产生滑转下陷,而车轮的牵引性能对机器人动力性、通过性具有重要影响,因此,深入分析车轮与松软地面之间的关系,对于研究轮式移动机器人的运动性能具有重要意义[1-3]。
轮-地接触实验工作量大,对诸多参数要求高,而仿真分析可以避免实验中的诸多不便。张锐、李建桥[4]通过将离散元分析软件和CAD软件结合,有效地模拟了各种复杂结构车轮、车轮行驶条件以及不同表面工作环境下的车轮/模拟沙土相互作用关系,并通过车轮运动性能测试平台实验获得验证。孙鹏、崔燚[5]采用离散元法分析梯形齿车轮在松软沙土表面的通过性,提出不规则形状颗粒群系统的离散元建模技术,建立了车轮牵引性能参数的细观表达式。高峰、李雯[6]用离散元方法模拟了低重力环境下的轮-地交互作用,推导出沙土推力的细观表达式,定量分析模拟沙土的可行驶性。 此外,国外学者也做了大量研究,Lav R Khot[7]等采用离散元法研究轮-地接触时沙土的变形特性,并用土槽实验验证了仿真结果。H Nakashina[8-9]等采用离散元方法预测车轮在不同滑转率下的牵引力和能够爬行的最大坡度,其仿真结果与实验结果具有良好的一致性。
本文利用离散元法对车轮的滚动性能进行分析,建立仿真分析模型,分析车轮与沙土颗粒接触时的应力分布及运动特性。
1 轮-地接触离散单元相互作用力学模型
离散元法将颗粒对象看作一系列离散的独立运动单元,单元之间以一定的接触力学模型构成,其运动由经典的牛顿第二定律控制。将研究对象离散成许多刚性圆盘或球形颗粒组成的试样,通过控制单个颗粒的运动以及颗粒之间的相互力,用显式时步迭代的方法,求解各个颗粒随时间的运动,以得到整个试样的力与变形规律[10]。相互接触的两个颗粒间的典型接触力学模型可以认为是由双弹簧-阻尼系统与切向摩擦力构成,如图1所示。
图 1 中 ,Kn和Ks分别为法向接触刚度和切向接触刚度,cn和 cs分别为法向接触阻尼系数和切向接触阻尼系数,fμ是摩擦因数。需要注意的是Kn为与总位移和力有关的正割模数,而Ks是与位移增量和力有关的正切模数,其中,cn和cs可以表示为:
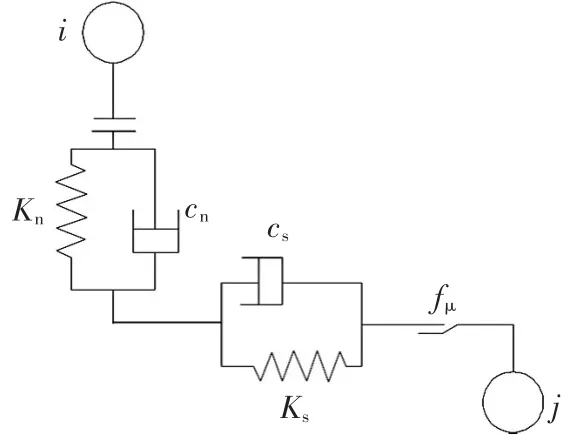
▲图1 离散元接触力学模型

2 车轮牵引性能仿真模型的建立
2.1 仿真参数
仿真模型的建立过程为:①确定颗粒的基本参数及接触参数;②生成土槽模型,并使颗粒达到自平衡状态;③生成车轮模型;④将车轮模型与土槽模型组合到一起,加入车轮驱动参数,开始仿真,输出必要的测量参数值。仿真模型参数见表1。
2.2 土槽建模
建立仿真模型时,二维颗粒离散元主要有两种几何元素,即球(Ball)和墙(Wall)。球体现为一个圆,被认为是刚体性,球与球之间通过点接触。墙体现为没有厚度的线,分为标准墙与一般墙。标准墙主要体现为一条直线,标准墙的一侧是激活的,即只有激活的一侧墙才可以与球接触产生作用力,标准墙可以用来模拟实际土槽的外壁。
本文以标准墙属性建立土槽的外围边界,土槽长0.8 m,高0.275 m。以球的指令生成模拟沙土颗粒。设定颗粒的最小半径为rmin=0.9 mm,最大半径为rmax=1.1 rmin,孔隙率为0.59,生成土槽的程序流程如图2所示。

表1 离散元仿真分析模型沙土参数

▲图2 土槽生成流程图
2.3 车轮建模
车轮模型包括光轮与带有齿片的车轮,本文采用墙的属性建立车轮模型。以一般墙模拟光轮,以标准墙模拟齿片,如图3所示。同时为了真实反映齿片与沙土直接作用状态,每个齿片采用起始点相反的两条标准墙模拟齿片。标准墙起始点的不同决定了墙激活面的方向,采用这种方式建立齿片模型,可以保证齿片的两个侧面均为激活面,真实反映齿片与沙土的相互作用。

▲图3 墙命令生成的车轮及齿片模型
2.4 车轮滚动性能仿真
车轮滚动性能仿真模型如图4所示。X轴正方向为车轮前进方向,土槽长0.8 m,高0.275 m,配置4层不同参数的沙土颗粒。设置作用于车轮上的载荷W=80 N,重力加速度取9.8 m/s2。设定光轮直径为0.27 m,齿片高度Lh分别为5 mm和10 mm,齿片间隔角度Ls=18°,齿片宽度为 7 mm。
由于车轮模型采用墙的方式建立,载荷不能直接施加到车轮上。在仿真过程中,依靠程序循环采集车轮与沙土间相互力的垂直分量,并不断与载荷大小进行对比来反映车轮的滚动状态。当垂直分力小于载荷时,车轮在X方向上的移动速度及转动角速度为零,设定车轮在竖直方向上的速度为-0.01 m/s,此时车轮沉陷;当垂直分力大于载荷时,车轮Y方向上的速度为零,设定X方向上的移动速度为0.01 m/s,此时车轮滚动前进。同时,给定车轮预期停止滚动时的位移动,并实时采集车轮的实际位移,当实际位移大于预定位移时,程序自动结束仿真。此时,输出车轮的位移信息、竖直方向的力、挂钩牵引力及驱动转矩,并保存该仿真分析过程文件*.sav,仿真流程步骤如图5所示。
3 车轮牵引性能离散元仿真结果分析
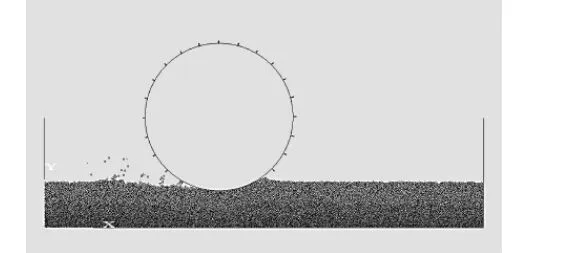
▲图4 车轮滚动性能仿真模型
图6 和图7为负载W=80 N、齿片间隔角度Ls=18°、齿片高度Lh分别为5mm和10mm时,车轮产生的挂钩牵引力PD与驱动转矩Tr的离散元仿真结果。
由图6可知,挂钩牵引力PD和驱动转矩Tr随着滑转率的增加而逐渐增大。

▲图5 车轮滚动性能仿真流程
由图7可知,挂钩牵引力PD和驱动转矩Tr随着滑转率的增加而逐渐增大。且与图6对比可知,齿片高度Lh由5 mm增加到10 mm时,挂钩牵引力PD与驱动转矩Tr显著增加。
4 结论
通过研究轮-地接触特性离散元法模拟仿真的机理及离散单元间相互作用的力学模型,建立车轮牵引性能仿真分析的模型。车轮滚动性能仿真结果直观反映出车轮对沙土颗粒的扰动状态,得到车轮与沙土颗粒接触时的运动特性关系。

▲图6 Ls=18°Lh=5 mm时滑转率S对挂钩牵引力PD和驱动转矩Tr影响的仿真结果

▲图7 Ls=18°Lh=10 mm时滑转率S对挂钩牵引力PD和驱动转矩Tr影响的仿真结果
[1] 谷侃锋,赵明扬.轮式移动机器人沙地行驶控制建模与仿真研究[J].系统仿真学报,2008,20(18).
[2] 邹猛.月球探测车辆驱动轮牵引性能研究[D].长春:吉林大学,2008.
[3] 庄继德.计算汽车地面力学[M].北京:机械工业出版社,2002.
[4] 张锐,李建桥.非规则车轮散体模拟月壤相互作用仿真系统研究[C].张家界:2012颗粒材料计算力学会议,2009.
[5] 孙鹏,崔燚.梯形齿车轮月面牵引性能的离散元分析[J].北京航空航天大学学报,2010,36(3):253-256.
[6] 高峰,李雯.模拟月壤可行驶性的离散元数值分析[J].北京航空航天大学学报,2009,35(4):501-504.
[7] Lav R Khot,Vilas M Salokhe.Experimental Validation of Distinct Element Simulation for Dynamic Wheelsoil Interaction[J].Journal of Terramechanics,2007,44:429-437.
[8] H Nakashina,H Fujii.Parametric Analysis of Lugged Wheel Performance for a Lunar Microrover by Means of DEM [J].Journal of Terramechanics,2007,44:153-162.
[9] H Nakashina,H Fujii.Discrete Element Method Analysis of Single Wheel Performance for a Small Lunar Rover on Sloped Terrain [J].Journal of Terramechanics,2010,47:307-321.
[10]刘一鸣,杨春和.考虑转动阻抗的粗粒土离散元模拟[J].岩土力学,2013,34(增刊 1):486-493.

