谈数学建模思想对大学数学教学作用的一点看法
周蕾
摘要:文章介绍了数学建模的思想方法,提出了将数学建模思想融入到高等数学日常教学中的意义,也说明了把数学建模的思想和方法融入到数学教学中确实是一种行之有效的素质教育方法。
关键词:数学建模;教学作用;能力
目前高等院校的大部分专业都开设了高等数学这门课程,但教学内容多,教学课时较少,学生学习过程中会感到相对枯燥无味,极易产生畏难情绪,学生积极性不高,极大地影响学习效果和教学质量。
近几年,许多院校正在将数学建模教学活动与教学类各主干课程有机结合起来,通过数学建模的思想方法来提高学生的综合素质以及研究与实践能力。
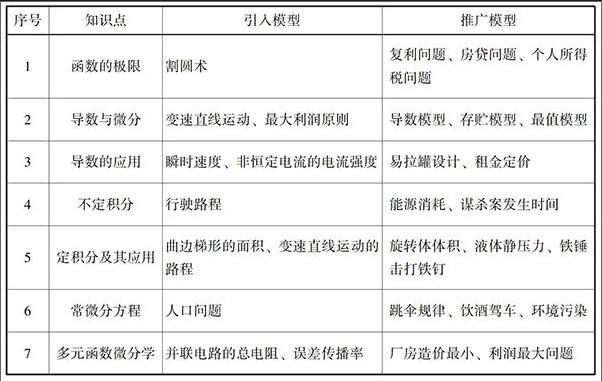
一、数学建模的思想方法数学建模没有统一的方法,但是针对实际问题,建立数学模型的基本过程大体相同,一般有以下几个步骤:①模型准备:认真分析所给实际问题,查找相关资料,收集相关数据。②模型假设:根据研究对象的特征及实际背景,抓住问题的本质,忽略次要因素,对问题做出必要的、合理的假设。③模型建立:根据做出的假设,以数学为工具,建立能够反映实际问题内在数量关系的数学模型。④模型求解与分析:把实际问题归结为一定的数学模型后,就要对模型进行求解与分析。在求解时,尽量采用各种现成的计算方法及各种计算工具,特别是数学软件与计算机技术。⑤模型检验与修改:将求解结果和分析结果反馈到实际问题中,并与问题的实际情况加以比较,如果吻合较好,则模序号知识点引入模型推广模型1函数的极限割圆术复利问题、房贷问题、个人所得税问题2导数与微分变速直线运动、最大利润原则导数模型、存贮模型、最值模型3导数的应用瞬时速度、非恒定电流的电流强度易拉罐设计、租金定价4不定积分行驶路程能源消耗、谋杀案发生时间5定积分及其应用曲边梯形的面积、变速直线运动的路程旋转体体积、液体静压力、铁锤击打铁钉6常微分方程人口问题跳伞规律、饮酒驾车、环境污染7多元函数微分学并联电路的总电阻、误差传播率厂房造价最小、利润最大问题型及其结果可以应用于实际问题;如果吻合不好,则需对模型进行修正,经过不断地修改和检验,直至得到合理的结论为止。因此,数学建模是“学数学”与“用数学”的统一,是一种微型科研的过程,是进行研究性学习的一种有效组织形式。
二、将数学建模思想融入到高等数学教学中的意义将数学建模思想融入到高等数学日常教学中的意义在于打破了原有的高等数学课程只重视理论,忽视应用的教学内容安排。在整个高等数学的教学过程中给学生展示了一个完整的数学,同时也全面地训练了学生的思维推理能力,使学生不仅学到了数学知识,而且增长了应用数学知识解决实际问题的本领。
1对教师的意义
(1)课堂上:数学建模的思想和方法同高等数学的课堂教学相结合离不开教师的主导作用。高等数学课的中心内容并不是要建立数学模型,我们只是通过数学建模强化学生的数学理论知识的应用意识,激发学生学习高等数学的积极性和主动性。所以,在编选教学案例时应从结合教学实际入手,达到既有助于学生理解教学内容,又可以使其用所学的数学知识解决实际问题的效果。
(2)习题上:下表中的推广模型可以作为习题,让学生自己发现问题,并用所学知识来解决这些实际问题。完成的形式可灵活处理,这样就可以通过习题渗透数学建模思想。比如,房贷的问题,学生就比较感兴趣,房子总价是A,首付了B,需贷款C,贷款的月利率D,每月都还,25年内还清,那么每月最少要还多少?通过分析,建立数学模型后,学生发现最后是用极限的知识求解的,当中还涉及等比数列的求和公式。而且,我们还发现现在房价是稳中有降,有更多的现实因素,如刚需、商家促销活动、政府救市等措施,由此展开出去,我们可以得到更复杂的模型,这样一步一步引导学生去思考,最后要求学生完成一篇小论文作为期末考试成绩的一部分。
(3)由于数学建模所涉及的数学知识体系较多、范围较广,教师的教学不再局限于课堂中知识理论的讲解,更要积极拓宽自己的知识范围,培养自身的创造性思维,熟练操作数学软件,不断更新知识和提高科研能力,从而为提高学员教师队伍素质和水平起到至关重要的推动作用。
2对学生的意义
(1)培养学生综合应用数学知识及方法进行分析、推理、计算的能力。数学建模的过程是反复应用数学知识与方法对实际问题进行分析、推理与计算,以得出实际问题的最佳数学模型及模型最优解的过程,因而学生明显感到自己这一方面的能力在具体的建模过程中得到了较大的提高。
(2)培养学生相互交流和文字语言、数学语言的表达能力。因为数学建模竞赛最终要以论文的形式交卷,能否在论文中将建模的思想与结果清晰地表述出来,将影响到参赛成绩的好坏。通过建模竞赛,学生们普遍感到语言表达能力及文字写作能力的重要。
(3)培养学生的创造力、联想力与洞察力。建模题材有较大的灵活性,没有统一的标准答案,学生可针对统一问题从不同角度、用不同的教学方法解决,因而有利于学生发挥其创新能力。此外,对于很多不同的实际问题,尽管其专业背景不同,在一定的简化层次下,它们的数学模型可以是相同或相似的,这就要求学生在建模时触类旁通,发挥其联想能力,挖掘不同事物间本质、相似的关系,从而用熟知、已有的数学知识及方法去建立模型。
(4)培养学生对已有科技理论及成果的应用能力。建模问题来源于社会的众多领域,但学生不可能熟知每一领域的专业知识。在建模过程中,他们需独立查阅相关的文献资料,进行针对性阅读并及时消化,将其应用到建模中来。此外,模型的求解往往需要用数值计算来实现,这样可促使学生为完成建模去利用现有的计算机技术及数学软件。
(5)培养学生团结协作精神的能力。要较好地完成任务,离不开良好的组织与管理、分工与协作;面对问题,要求队员们相互理解、相互尊重,共同探讨,彼此协调以求共识,从而最大限度地提高集体的知识容量、达到较高的工作效率。因而在建模过程中,学生必须学会如何与别人合作以谋求最大成功,如何清楚地表达自己的思想,如何接纳别人的见解以发挥整体的作用。
现在我国许多高校都开展了大学生数学建模活动,学生通过参加数学建模的实践促使他们更好地应用数学、品味数学、理解数学和热爱数学。这也说明了把数学建模的思想和方法融入数学教学中确实是一种行之有效的素质教育方法。
参考文献:
〖=1〗姜启源,谢金星,叶俊编.数学模型(第三版)〖=M〗.北京:高等教育出版社,2006.
〖=2〗贾晓峰,杨晋,张明学.大学生数学模型竞赛与高等学校数学教学改革〖=J〗.工科数学,2000(02):79—82.endprint

