掺杂PZT压电振子弹性疲劳的导纳圆表征法*

陈如麒，朱贵文，沈文彬，陈 敏

(1.华南农业大学公共基础课实验教学中心，广东广州 510642;2.广东药学院基础学院物理与电子学教研室，广东广州 510006;3.中山大学物理科学与工程技术学院，广东广州 510275）

在交通、航空、航天、机械等诸多应用领域，电子元器件都是在电场和力场并存情况下工作，它们长期共同作用使得材料的结构改变、性能失效的主要原因。电力场共同作用下弹性疲劳研究是当今热点之一［1－4］。据相关报道，目前一般采用弯曲疲劳测试法［5－6］、球压法［7］、拉 － 压法［8－9］、多场耦合试验法来研究材料弹性疲劳特性［10］。然而，弯曲疲劳测试法、球压法、拉－压法、对于测量片状或者是薄板型陶瓷材料不适合，它无法表征真实应力下的弹性疲劳，在测量过程中陶瓷片夹持点不易控制，对频率影响很大。多场耦合试验法适合测量陶瓷材料，但是它检测前需要设计测试模具、搭建实验装置，测试成本较高。

导纳圆法测试陶瓷片状材料、夹持点容易定位、实验设备简单、检测成本低，可克服上述测试疲劳方法的不足，更为全面地表征材料疲劳的参数［11－12］。本文用具有高介电常数、压电、热释、光学性能的掺杂锆钛酸铅 (PZT)陶瓷片作为研究对象［13］，用导纳圆法来表征其弹性疲劳特性，从而建立一种定量描述弹性疲劳的检测方法。

1 弹性疲劳

一个理想的固体，其形变位移与外加作用力成正比。当固体在外力长期作用后除去外力时不能回复其原来形状尺寸，就出现弹性疲劳;此时，它的弹性系数也出现变化。一个压电陶瓷在周期性外电压作用下经历很长时间后出现的弹性疲劳和铁电疲劳一起，还将引起压电疲劳;其表现为压电系数和机电耦合系数发生了变化。当外电压变化一个周期时，外加作用反转了两次。故在压电疲劳中，样品的弹性系数、压电系数和机电耦合系数都可描述为外加作用反转次数N的函数［14－15］。

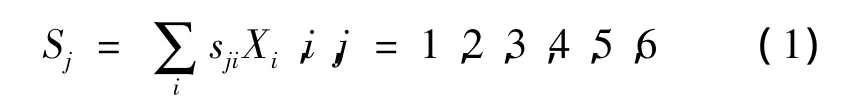
固体在外应力Xi作用下产生的线性应变可写成式中，sji为弹性顺度常数 j=1，2，3 时 Sj为 x，y，z方向的正应变。j=4，5，6 时 Sj为垂直于 x，y，z方向的切应力。36个常数随N的变化，sji(N)描述了弹性疲劳效应。实验研究就是要测出这些函数。在压电研究中，已经找到了分别测量压电体的不同弹性顺度常数sji的方法。

由于样品的对称性要求，36个sji一般地不是互相独立的。对于压电陶瓷，将sji写成矩阵形式，其独立参数可表示为

本文将讨论压电陶瓷的弹性顺度常数s11的测量方法。

掺杂PZT压电振子工作在机械谐振点电路中，观察样品在强烈机械共振情况下作N次伸长和缩短的弹性形变后，用导纳圆图法作出谐振频率fR，然后根据公式计算出描述弹性疲劳参数s11的值。一般来说弹性疲劳是在外加作用下，体系中的杂质和缺陷趋向集中于应力较大区域，致使弹性顺度常数s11增大。增大至一定程度后，小小的应力即足以使体系发生断裂。

2 PZT压电振子实验结果和讨论

实验用来研究压电疲劳的样品是邮电部生产的用于机械滤波器的掺杂PZT压电陶瓷片;其厚度为a=0.70 mm，宽度为b=2.66 mm，长度为l=29.52 mm;a＜＜b＜＜l。陶瓷片两面烧银电极。样品密度ρ=7.6 g/mm3。用1 kHz测得低频电容C=1.0190 nF，tan δ=0.0237。压电振子的等效电路如图1所示，其电导记为G，电纳记为B。利用HP4192A阻抗分析仪在样品电极上加频率为f的正弦电压，可测得样品的G和B值;(G，B)给出复平面上的一个点。可以证明，当f由低频单调增大时，测点按顺时针方向扫过(G，B)复平面上的一个圆周，参见图2(a);称之为导纳圆。导纳圆和G轴相交于点R和A，相应的频率为谐振频率fR和反谐振频率fA。用不同频率f测得的(G，B)测点示于图2(b)，所有测点很好的分布在一个圆周上，其标出了导纳圆心的位置。在压电振子的导纳圆心上，应有G＞0和B＞0。这说明关于压电振子导纳圆的理论是可信的。

图1 压电振子的等效电路Fig.1 Equivalent circuit of piezoelectric vibrator

由图2可估计出原始样品有fR=57.4 kHz，fA=58.8 kHz

当压电振子在共振区附近共振时［16］，

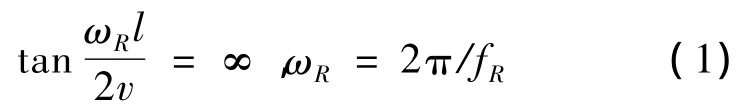
可以得到一系列谐振频率

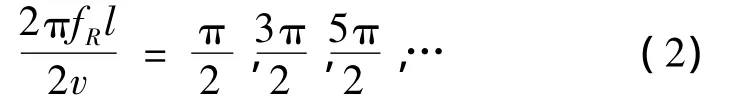
再由压电振子中纵向弹性波的传播速度

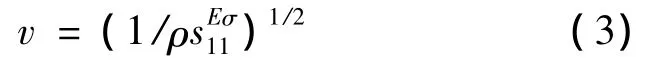
根据式 (1)、(2)、(3)可推出弹性顺度常数表达式为

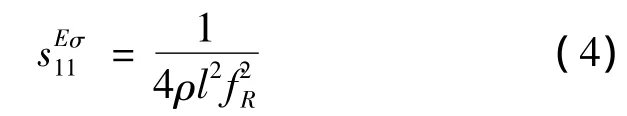
图2 导纳圆图(a)和(b)导纳圆的测量结果(N=0)Fig.2 Admittance circles(a)and

可计算出原始状态 (N=0，N为伸长或缩短次数)时的弹性顺度常数=1.14×10－11(m2/N)。

在测量中，长度为l的压电振子用金属弹簧支持在的中点A和B上，安装方法如图3所示。A和B兼作外加电压的两个电极。当外电压频率为fR时，压电效应激发了沿l方向的长度变化机械谐振;此时，样品的两个自由端是波腹，振动位移量最大，方向相反，如图3箭头所示。而支点A和B恰在不出现振动位移的波节上。若测量时弹簧对样品的夹持点偏离了A和B，测出的fR值会出现错误;而得到的“导纳圆”也会严重变形。

压电振子的安装Fig.3 Installation of piezoelectric vibrator

图4 压电谐振区的振荡电路Fig.4 Oscillator circuit in piezoelectric resonance region

当样品被强迫作N次伸缩振动后测出低频电容C，谐振频率fR和反谐振频率fA。由此计算出低频弹性顺度常数。经历N次极化反转后，以logN为横坐标;×1012为纵坐标作出掺杂PZT材料的弹性疲劳参数示于图5。

图5 PZT材料的弹性疲劳参数Fig.5 Parameters of elastic fatigue for PZT

4 结论

根据式 (4)，ρ和l不随N而变化。由实验测得fR(N)随N增大而单调减小，故必随N增大而单调增加。说明了空位和缺陷都向应力集中的地方扩散。这已初步表现出弹性疲劳。用导纳圆法定量研究了PZT压电陶瓷的弹性疲劳。证实当PZT工作于谐振频率下，则N＞109时出现明显的疲劳，弹性顺度常数s11随N的增大连续单调地增加，则导纳圆法有可能发展成为一种弹性疲劳的无损检测方法。

［1］HAINES J，BORMAND J，PINTARD V，et al.Pressure tuning of the morphotropic phase boundary in piezoelectric lead zirconate titanate［J］.Physical Review B，2007，70(1):14108－14111.

［2］FU R，QIAN C F，ZHANG T Y.Electrical fracture toughness for conductive cracks driven by electric fields in piezoelectric materials［J］. Applied Physics Letters，2000，76(1):126－128.

［3］TEIXEIRA E C，PIASCIK J R，STONER B R.Dynamic fatigue and strength characterization of three ceramic materials［J］.Journal of Materials Science Materials in Medicine，2007，18(6):1219 －1224.

［4］RAMALINGAM S，REIMANIS I E，FULLER E R.Slow crack growth behavior of zirconia-toughened alumina and alumina using the dynamic fatigue indentation technique［J］.Journal of American Ceramic Society，2011，94(2):576－583.

［5］SEDRAKIAN A，BEN ZINEB T，BILLOET J L.A numerical model of fatigue behavior for composite plates:application to a three point bending test［J］.International Conference of Fatigue of Composite，1997，3(5):415 －423.

［6］CAPRINO G，AMORE A D.Flexural fatigue behavior of random continuous fibre-reinforced thermoplastic composites［J］.Composites Science and Technology，1998，58:957－965.

［7］PEDERSEN T O，TVERGAARD V.On low cycle fatigue in metal matrix composites［J］.International Journal of Damage Mechanics，2000，9(2):154 －173.

［8］CAPRINO G.Predicting fatigue life of composite laminates subjected to tension-tension fatigue［J］.Journal of Composite Materials，2000，34(16):1334 －1355.

［9］GAMSTEDT E K，SJOGREN B A.Micromechanisms in tension-compression fatigue of composite laminates containing transverse plies［J］.Composites Science and Technology，1999，59(2):167－178.

［10］邓启煌，王连军，王宏志，等.锆钛酸铅陶瓷在力电耦合场下疲劳性能的评价［J］.无机材料学报，2012，27(4):358－362.

［11］COLE K S，COLE R H.The complex dielectric constant［J］.J Chem Phys，1941，9:341 －351.

［12］范仰才，李景德，符德胜.广义导纳圆［J］.中山大学学报:自然科学版，1995，34(3):31－35.

［13］WARREN W L，DIMOS D，TUTTLE B A.Polarization suppression in Pb(Zr，Ti)03thin films［J］.J Appl Phys，1995，77(12):6695－6702.

［14］李景德，沈韩，陈敏.电介质理论［M］.北京:科学出版社，2003:240－244.

［15］李景德，郭宏凯.压电振子和水声谐振腔的耦合［J］.压电与声光，1993，15(2):47－53.

［16］殷之文.电介质物理学［M］.2版.北京:科学出版社，2003:246－262.