透过率起伏频谱空间相关法颗粒测量技术

万 宸， 沈建琪， 郭露芳， 贾晓伟

（上海理工大学 理学院，上海 200093）

透过率起伏频谱法（TFS）采用窄光束作为入射光照射颗粒，由于颗粒对光的散射和吸收，透射光信号会产生剧烈的波动.通过对透射光信号进行时间或空间平均处理，可获得透过率期望值ETS［1－5］.改变平均参数，ETS 会形成一个频谱，从该频谱中可提取颗粒粒径及浓度信息［4］.对于透过率起伏频谱相关法则采用透过率起伏信号的自相关或互相关处理来代替信号平均处理［6－9］.在自相关技术中，只需用一束窄光束作为入射光，透过率信号 T（t）随时间变化，通过信号的自相关计算可以得到不同时间对应的透过率的乘积T（t）T（t＋τ）.因此改变相关时间可得到ETP 自相关频谱.这种方法被称为透过率起伏频谱时间相关法或自相关法（TFS－TC or TFS－AC）［7］.在互相关技术中，需要用到两束窄光束作为入射光，相应的ETP 为该两束光透过率的乘积.改变两束光的间距同样可获得ETP 互相关频谱.这种技术被称为透过率起伏频谱空间相关法或互相关法（TFS－SC or TFS－CC）［9］.在时间相关法中，实验光路非常简单，但是要通过该方法获得颗粒粒径及浓度信息，必须事先测量流体的流速，且实验结果往往会受到测量区流速的影响，故透过率起伏频谱时间相关法（TFS－TC）只适用于层流情况，这在很大程度上限制了该方法的应用.对于透过率起伏频谱空间相关法（TFS－SC）则不需要事先知道流体流速，但两束光间距的机械调节需要在微米级范围内并且要求与信号采集同步，同时，两束光的直径和传播方向应完全一致，这在实际中很难实现［7］.

本文设计并实施了一种新的透过率起伏空间相关测量方法，该方法采用线光源照射待测样品，用线阵CCD 传感器接收透射光信号，经过空间平均处理可得到空间相关谱，通过该频谱可获得颗粒粒径、浓度、速度信息.

1 透过率起伏频谱空间相关法的理论推导

根据层结构模型［3］，三维颗粒系可看成是一系列单层颗粒的堆积，因此，三维颗粒系的透过率期望值ETS 和透过率乘积ETP 的计算可基于单层颗粒情况来描述

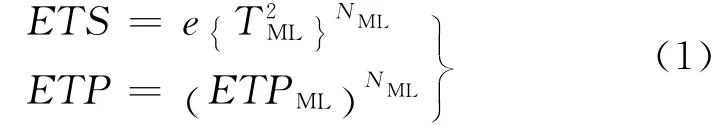
式中，ML 为颗粒层；NML为颗粒系统的层数，定义为［10］

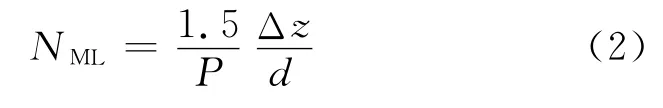
式中，P 为结构参数，且大于1.5；d 为颗粒直径；Δz为颗粒系在入射光传播方向上的厚度；Pd／1.5 为单层颗粒的厚度.

为方便研究，首先假设单层颗粒系含有粒度均一的完全吸收性球形颗粒，层厚度不小于颗粒粒径.所有颗粒在层中随机分布且不互相重叠，如图1所示.

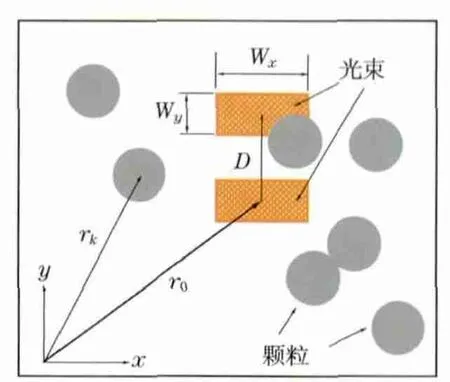
图1 单层颗粒系统原理图Fig.1 Schematic diagram of the monolayer

据几何光学原理，透过率可通过函数描述为

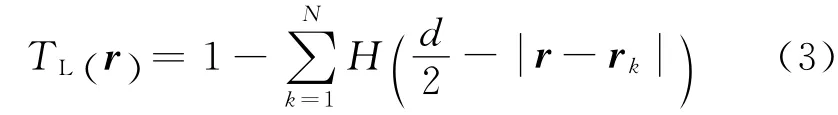
式中，N 为颗粒个数；rk为某个颗粒中心的坐标，Heaviside函数定义为

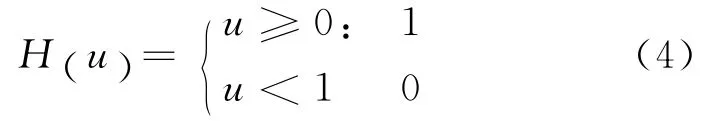
对于矩形光束来说，透过率就是透射光强在光束横截面上取空间平均，即

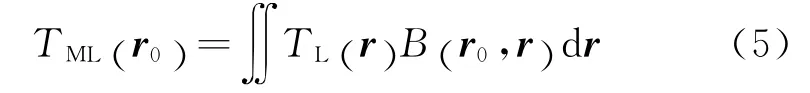
式中，Wx，Wy为矩形光束横截面在x 和y 方向上的长度.这里矩形函数定义为

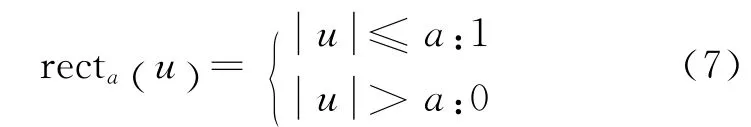
因此，对于间距为D 的两束光，透过率相关乘积可表示为

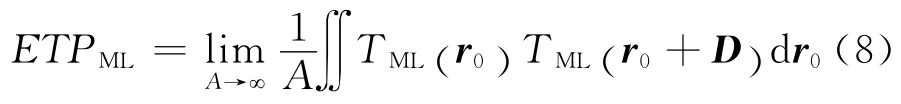
式 中，A 为 层 面 积.根 据Rayleigh 原 理，ETP 在 傅里叶空间里表示为

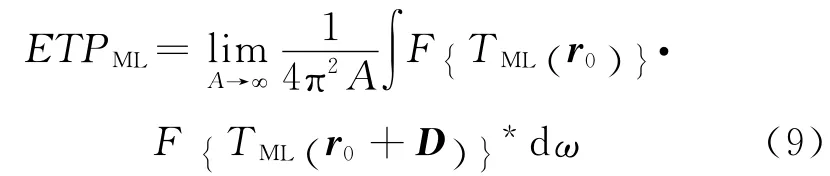
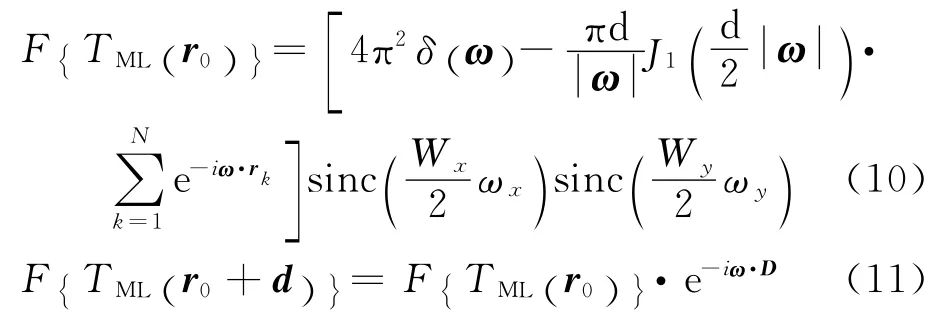
假设两束光间距D 沿y 方向，经过一系列繁复的演算，可以得到通过单层颗粒的透过率相关乘积

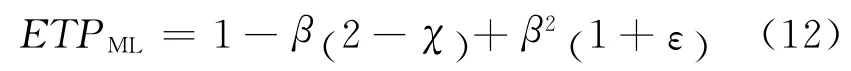
式中，β 为层密度，表示球形颗粒在层面上的投影面积与层面积的比率［10］

式中，CV为颗粒系的体积分数.式（12）中，χ，ε 是特征函数，描述的是透过率起伏频谱特征，其表达式为

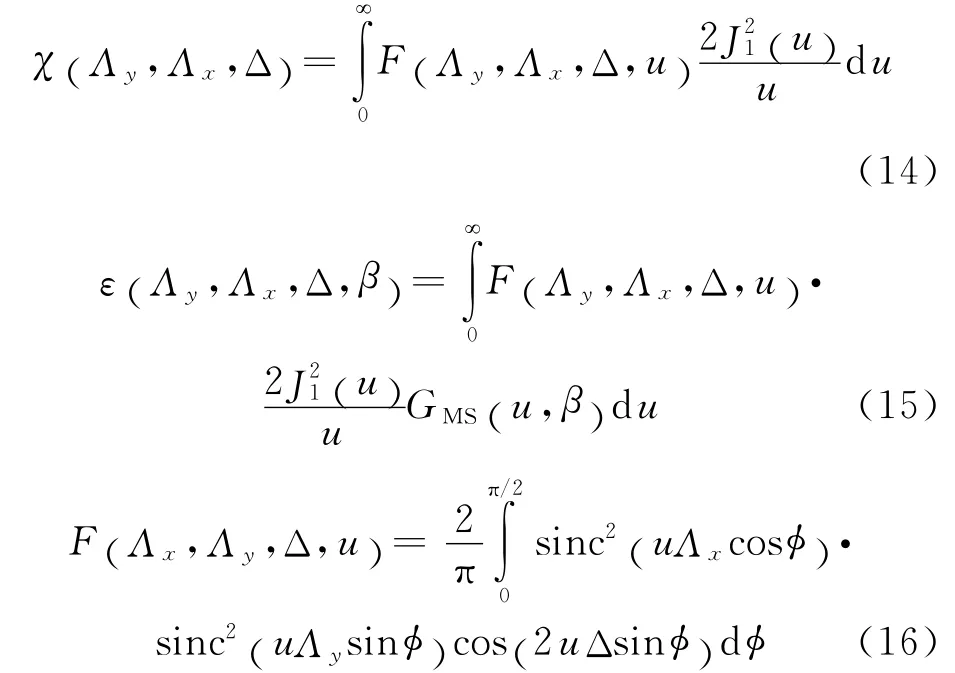
式中，Δ＝d／x 为无因次光束间距（相关参数）；Λx＝Wx／d，Λy＝Wy／d 分别为在x 和y 方向上光束的无因次边长；J1是Bessel函数是层结构因子［11］.当颗粒浓度足够低时，式（12）可简化为

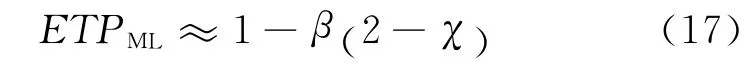
因此，对于三维颗粒系统，同理可得

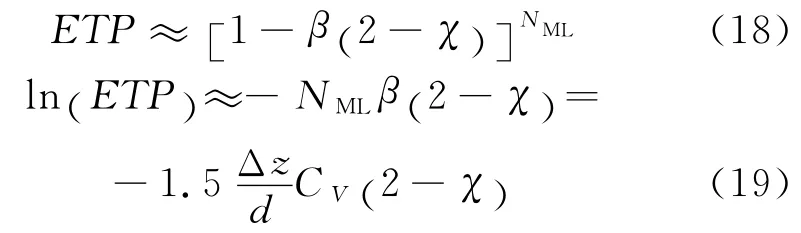
上述模型基于系统中所有颗粒具有相同的粒度（即单分散颗粒系）.对于多分散系颗粒系统，可将不同粒径的颗粒划分到相应的粒径区间，每个粒径区间可看成单分散颗粒系.因此，多分散颗粒系的透过率可看作一系列不同的单分散系颗粒系的透过率的累积.式（19）可改为

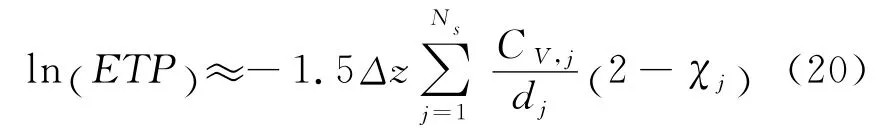
2 特征函数的数值计算及讨论

根据透过率起伏频谱法原理，可以从透过率起伏频谱中获得颗粒粒径信息.在低浓度情况下，透过率起伏频谱主要由特征函数χ 来描述.图2即给出了特征函数χ 的数值计算结果.当光束直径远小于颗粒粒径（Λx＝Wx／d＝0，Λy＝Wy／d＝0）时，单个颗粒就能够完全遮盖住入射光，因此透过率信号为0或1，分别对应在光束传播路径上此时有颗粒或无颗粒情况.当相关参数为零时（Δ＝0），透过率相关乘积ETP 就是透过率期望值ETS 本身，因此，由式（18）可得到

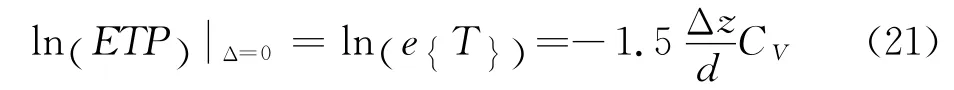
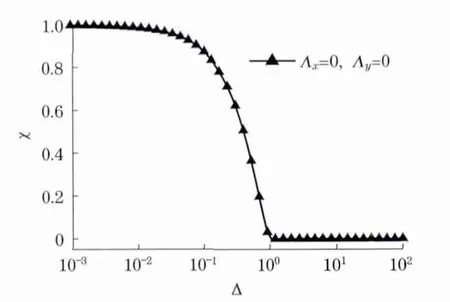
图2 特征函数χ 的数值计算结果Fig.2 Numerical results on the transition function

从图2可以看到，在无限细光束（Wx＜＜d，Wy＜＜d）情况下，其中，Λx＝Λy＝0，当Δ＝0时，χ＝1.这里相关参数为零意味着两束光完全重合，此时两束光信号完全相关.随着相关参数的增大，两束光信号的相关性逐渐减小，因而特征函数χ 的值也逐渐减小.当相关参数大于1时（D≥d），两束光的透过信号相关性完全消失.此时，透过率相关乘积等于透过率平均值的平方.相应的特征函数χ＝0.

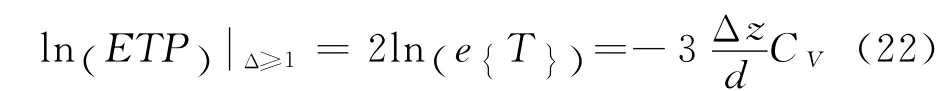
当特征函数降为零时，此时的相关参数的大小反映出颗粒的粒径.同时，颗粒的浓度信息可从式（21）和式（22）中得到.因此，可从透过率起伏空间相关谱中获得颗粒的粒径及浓度信息.

图3（见下页）是特征函数χ 在不同的光束直径情况下的数值计算结果.图3（a）中，Λx＝1.0，Λy从1变到10，图3（b）中，Λy＝1.0，Λx从1变到10.从图中可以看到，当光束横截面变大时，由于透过信号在光束横截面上的空间平均，特征函数在Δ＝0 时的值逐渐减小，降低了透过率起伏频谱的分辨率.综上所0 述，在运用透过率起伏频谱空间相关法（TFS－SC）时，为提高分辨率，最好采用较小直径的光束（光束直径不远大于颗粒粒径）.从图3（a）中还可以看到，随着光束在y方向上的长度Wy增加，谱线的折点会向相关参数值增大的方向漂移.而光束在x 方向上的长度Wx的改变则不会影响谱线的折点.总的来说，当D≥Wy＋d（或Δ≥Λy＋1）［12］时，透过率信号间的相关性完全消失.因此，在TFS－SC测量技术中，选择合适的光束直径对于颗粒粒径的测量非常重要.

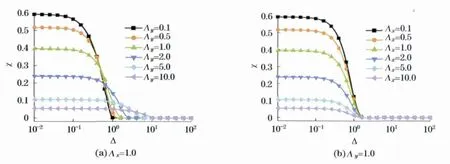
图3 特征函数的数值计算结果Fig.3 Numerical results on the transition function

图4给出了包含两种不同粒径颗粒分散系的透过率起伏频谱的数值模拟结果.矩形光束边长满足Wx／Wy＝0.1.两种颗粒粒径分别为d1＝0.5Wy和d2＝5Wy，体积分数分别为CV，1＝0.03 和CV，2＝0.1.从图中可以看到，当两种颗粒粒径比很大时（如d2／d1＝10），很容易在谱线上看到有两个折点P1和P2.对于较小的颗粒（如粒径信息），可以从谱线的左边部分得到.同样，对于较大的颗粒（如粒径信息），可以从两折点P1和P2之间那部分谱线中得到.当然，图4描述的是比较简单的情况，对于多分散系颗粒系统，谱线中的折点不会这么明显，需要用反演算法［13－14］来从谱线中提取粒径分布和浓度信息.

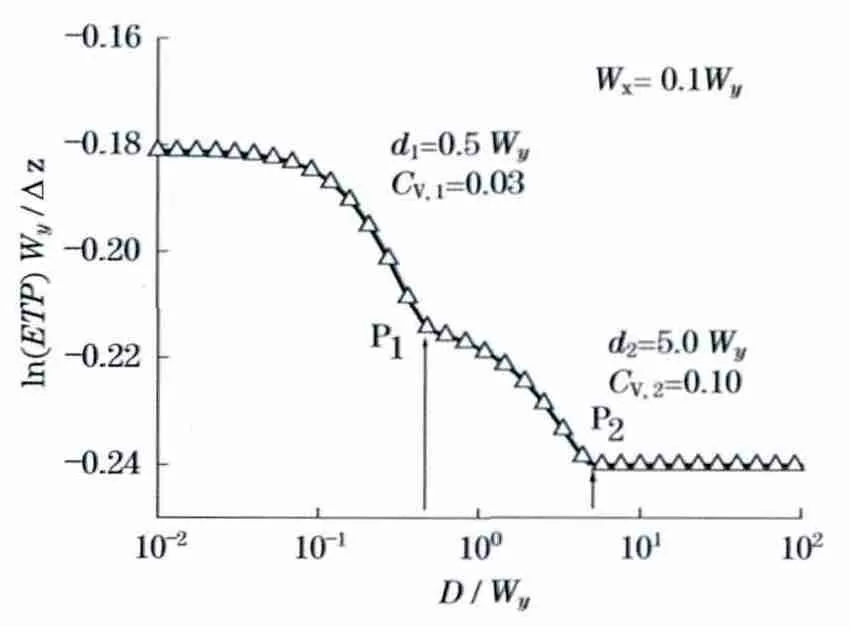
图4 双分散系颗粒系统透过率起伏频谱数值模拟结果Fig.4 Simulated transmission fluctuation spectrum for the Bi－modal particle dispersion

3 实 验

图5给出测量光路图，采用单模光纤激光器为光源，从激光器射出的光束经扩束器（由两不同焦距的凸透镜组成）扩束后，透过狭缝光阑形成一束矩形光束，狭缝的边长分别为Hx＝2mm 和Hy＝20mm.矩形光束经过第一个柱面透镜GL15－020－150后，在x方向上会聚而y方向上光束宽度不变.在柱面透镜焦平面上形成一条与y轴平行的线光束，样品池放置在该焦平面上，使得样品池中的颗粒被线光束垂直照射，通过样品池的透射光最后被另一个柱面透镜GL15－020－100会聚在CCD传感器上.实验中所测样品为自制的海藻酸钠球形颗粒［9］，为近似的单分散系颗粒，粒径d＝2.75mm，测量时放入一个闭合的循环系统，循环系统的动力由真空气泵（PCF5015N）提供且流速可调.透射光的探测器采用线阵 CCD 传感器（NEC 公司的型号μPD3575D，像素1024），其像元大小为14μm×14μm的正方形，两相邻像元中心的间距为14μm.

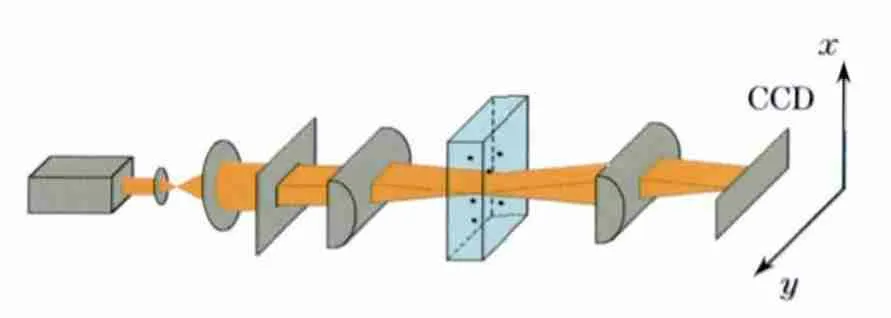
图5 透过率起伏频谱空间相关法实验装置图Fig.5 Experimental setup for the TFS technique with spatial correlation

实验分两步进行：第一步，未加入颗粒时测量透射光信号作为背景光信号；第二步，加入颗粒后的透射光信号测量.每一个像元的透过率Ti就是测量得到的透射光信号与背景光信号的比值，脚标i 表示像元序号（i＝1，2，…，1024）.对于单次测量，对信号做互相关处理

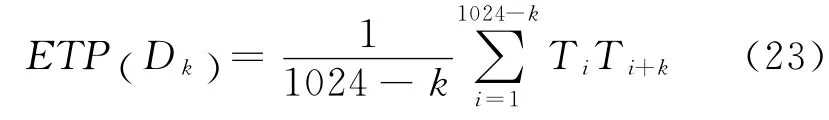
相关光束间距取两个像元的间距，即Dk＝14曲线就是所谓的透过率起伏空间相关谱.为了使测得的谱线更加稳定，需要对透射光进行多次测量然后求平均，实验中重复测量次数M ＝1000，即

由于线光束与y 轴平行，根据几何光学原理，该线光束在y 方向上可看成由许多细光束叠加而成，每束细光束在y 方向上的长度Wy正好等于像元的边长（Wy＝0.014 mm）.光束在x 方向上的长度Wx随着光束的传播，变化相对比较复杂.狭缝光阑的开口宽度Hx＝2 mm，第一个柱面透镜的焦距f＝150 mm，根据夫琅和费衍射，矩形光束在x 方向上的宽度Wx在焦平面位置为0.07 mm，这里所用激光波长λ＝0.658μm，水的折射率n＝1.33，测量区的厚度Δz＝10 mm.实验中考虑到光束的宽度Wx在测量区中并非均匀，而是先会聚后发散，因此，通过计算得到Wx在测量区中的平均值远小于所测颗粒的粒径（2.75 mm）.在测量区中矩形光束的横截面积近似等于10－3mm2，同样远小于所测颗粒的投影面积（σP＝πd2／4＝5.9 mm2），满足原理中所要求的光束直径远小于待测颗粒粒径.

4 实验结果分析

4.1 不同颗粒浓度情况

图6给出了不同颗粒体积分数下的测量结果.在图6（a）中，可以看到频谱转折点位于Dk＝3mm附近，接近所测样品颗粒的粒径（d＝2.75mm），该差别可能源于光束在y 方向上的不严格平行；转折点右侧谱线有轻微的振荡.

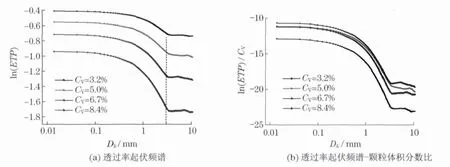
图6 透过率起伏频谱空间相关法测量不同浓度颗粒的实验结果Fig.6 Experimental results on the transmission fluctuation spectra under different particle concentrations

图6（a）中谱线高度反映了颗粒的浓度信息.此时系统在x 方向的流速为7.5L／min.根据式（19）可知透过率起伏频谱与颗粒体积分数成正比，即透过率起伏频谱与相应的体积分数之比曲线应互相重合，如图6（b）所示.实验结果和理论基本吻合，除了在低体积分数（3.2%）时的结果.这可能是由于测量区的颗粒浓度在很大程度上受流场情况影响.在上述测量过程中，由于颗粒在x 方向流速较慢，使得颗粒在循环系统中分布不均匀，在测量区形成颗粒的堆积，因而导致图6（b）中的偏差.

4.2 不同颗粒流速和流向情况

实验还测量了颗粒浓度恒定时颗粒系统在不同流速和不同流向时的透过率起伏频谱.测量结果见下页图7（a），此时颗粒流向沿x 轴方向，体积分数为6.3%.可以看到，不同流速情况下透过率起伏频谱基本重合.

当改变颗粒在测量区中的流动方向，测得透过率起伏频谱见下页图7（b）.此时，系统体积分数为3.2%，颗粒流速为7.5L／min.可以看到，所得谱线基本不变.

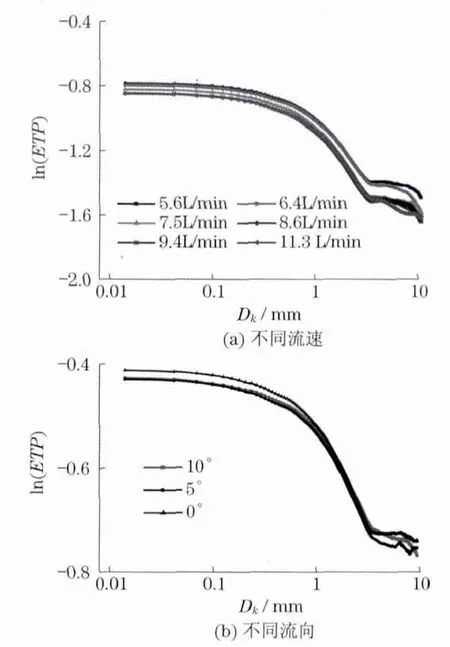
图7 不同流速和流向下的透过率起伏频谱Fig.7 Transmission fluctuation spectra measured in different flow velocities and directions

在不同颗粒浓度、不同流速和流向情况下测量得到的透过率起伏频谱表明：测量结果和理论相吻合，证明了空间相关法颗粒测量技术不受流场的影响.

5 结 论

设计并实施了一种新的透过率起伏频谱空间相关法颗粒测量装置.该装置的核心就是用线光束作为入射光照射颗粒，从而省去了空间相关法中两束光间隔的机械操作，在很大程度上提高了测量效率和精度，使得透过率起伏空间相关频谱法颗粒测量技术在实际中得以实现.实验结果验证了理论的可行性，透过率起伏频谱不仅能够反映出颗粒粒径及浓度信息，而且证明了透过率起伏频谱空间相关法（TFS－SC）颗粒测量技术不受流场流速和流向的影响.需要指出，测量过程中采用线光束作为入射光且颗粒粒径比较大的情况.光束在y 轴方向的宽度维持不变，因此光束在y 轴方向上的尺寸和CCD 传感器像元几乎一致.对于测量较小颗粒，可以考虑在y轴方向上发散线光束作为入射光，这将在后续研究中讨论.此外，本文实验中所测量的是单分散系颗粒，后续研究将考虑多分散系小颗粒情况.

［1］Breitenstein M，Kräuter U，Riebel U.The fundamentals of particle size analysis by transmission fluctuation spectrometry［J］.Part Part Syst Charact，1999，16（6），249－256.

［2］Breitenstein M，Riebel U，Shen J Q.The fundamentals of particle size analysis by transmission fluctuation spectrometry［J］.Part Part Syst Charact，2001，18（3），134－141.

［3］Shen J Q，Riebel U.The fundamentals of particle size analysis by transmission fluctuation spectrometry［J］.Part Part Syst Charact，2003，20（2）：94－103.

［4］Shen J Q，Riebel U.Particle size analysis by transmission fluctuation spectrometry［J］.Part Part Syst Charact，2003，20（4）：250－258.

［5］Shen J Q，Riebel U，Breitenstein M，er al.Fundamentals of transmission fluctuation spectrometry with variable spatial averaging［J］.China Particuology，2003，1（6）：242－246.

［6］Shen J Q，Riebel U，Guo X.Transmission fluctuation spectrometry with spatial correlation［J］.Part Part Syst Charact，2005，22：24－37.

［7］Shen J Q，Riebel U A，Guo X.Measurements on particle size distribution and concentration by transmission fluctuation spectrometry with temporal correlation［J］.Opt Lett，2005，30（16）：2098－2100.

［8］Guo X A，Riebel U.Experimental study on particle size distribution and concentration using transmission fluctuation spectrometry with the autocorrelation technique［J］.Part Part Syst Charact，2005，22（3）：161－171.

［9］Guo X A. Transmission fluctuation correlation spectrometry［D］.Cottbus：BTU Cottbus，2007.

［10］Breitenstein M.Grundlagenuntersuchung zur Statistischen Partikelgöβenspektrometrie mittels Auswertung der Transmissionsfluktuationen von Licht in Dispersen Systemen［D］.Cottbus：BTU Cottbus，2000.

［11］Shen J Q， Riebel U. Transmission fluctuation spectrometry in concentrated suspensions［J］.Part Part Syst Charact，2004，21（6）：429－439.

［12］沈建琪，蔡小舒，于彬.消光起伏自相关频谱法颗粒测量技术［J］.工程热物理学报，2006，27（5）：795－798.

［13］Shen J，Yu B，Wang H R，et al.Smoothness－constrained projection method for particle analysis based on forward light scattering［J］.App Opt，2008，47（11）：1718－28.

［14］Ferri F，Bassini A，Paganini E.Modified version of the Chahine algorithm to invert spectral extinction for particle sizing［J］.App Opt，1995，34（25）：5829－39.