基于ANSYS压力容器不等厚过渡区的强度优化

苏文献， 许 伍

（上海理工大学 能源与动力工程学院，上海 200093）

压力容器通常是由板、壳组合而成的焊接结构，是化工、石油、冶金、轻工、纺织等领域中广泛使用的承压设备［1－2］.在实际应用中，设计的压力容器总是存在过渡区（即不连续区域），如封头与壳体焊接区、隔板与壳体焊接区及接管补强区等.在载荷作用下，过渡区由于变形不协调产生了附加的边缘力和边缘力矩，以及抵抗这种变形的局部应力，导致这些区域的总应力增大，出现了应力集中现象，使得这些区域容易发生强度和疲劳失效.但是确定过渡区域理论解是有很大难度的，而且由于实验的条件限制或者结构的复杂性使得实验测量非常困难和昂贵.有限元理论的发展克服了这些问题，目前国内外诸多学者利用有限元法对多种结构进行应力分析和优化设计［3－5］.在传统的容器设计领域中，为了保证容器的安全性，设计者总是想通过增加容器的壁厚以增强容器的承压能力.随着优化分析设计方法概念的提出，在传统设计的基础上，进行压力容器的优化设计越来越成为化工容器设计的趋势.优化设计是一种在满足限制条件下寻找结构最优化的设计方法.本文应用有限元软件ANSYS结合优化设计方法，对容器的过渡区域进行应力计算和优化设计.

1 ANSYS优化设计理论

优化设计模块OPT 是ANSYS软件包集成的可以用于结构优化设计分析的模块，和APDL 语言一起发挥ANSYS优化设计的功能.

1.1 设计优化的3种变量

在ANSYS优化设计过程中存在3种类型的变量：设计变量、状态变量和目标函数.

优化分析中的独立变量是设计变量，设计变量可以表示成矢量形式

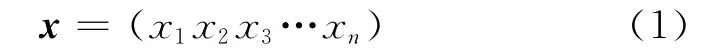
同时，设计变量受到多个具有上下限的约束条件的限制，即

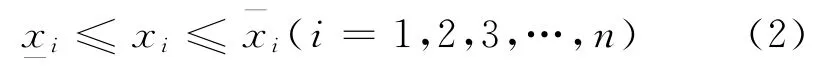
状态变量通常叫做可行的设计空间，用于约束设计变量.在可行性的设计空间中使得目标函数最小化

约束

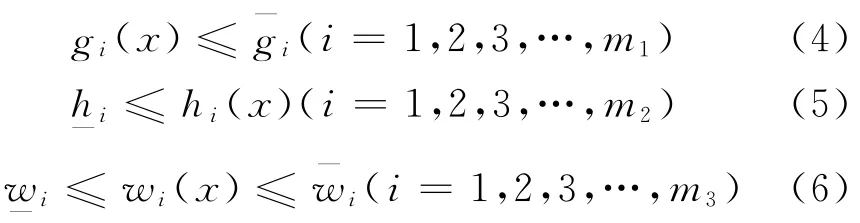
式中，f 为目标函数；gi，hi，wi为状态变量，顶线和底线分别表示上下限边界；m1＋m2＋m3为状态变量的个数.

状态变量也可以看作成独立变量，当然也随着设计变量x的变化而变化.式（3）旨在使目标函数f在式（2）～（6）约束下取得最小.

1.2 可行和不可行设计方案

满足所有约束的方案是一个可行方案；若设计方案不满足一个或几个约束是一个不可行的方案.在预定义的可行性的分析空间内，一个允差被加到每一个状态变量限上，即

只要满足式（8）、式（9）和式（11），设计被认为是可行的，即

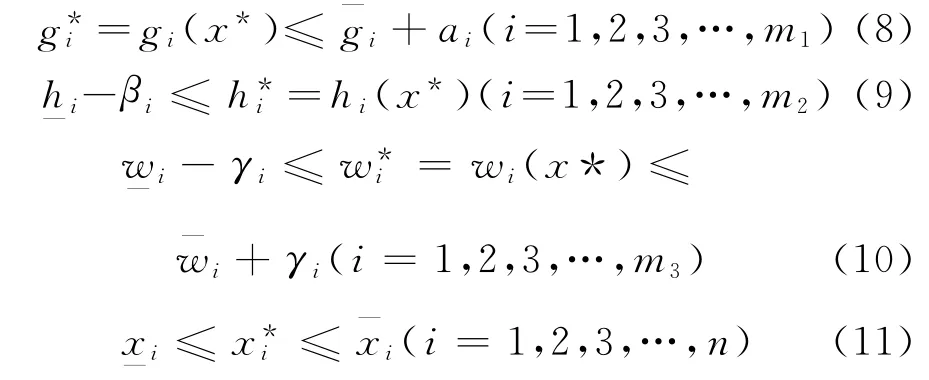
式中，αi，βi，γi为允差.

1.3 最优化的设计方案

满足以下两个条件中的任一条件就是最优化的设计方案：

a.当存在一种或者多种可行方案时，最优化的设计方案是使目标函数最小的方案，也就是说，满足式（3）～（6）的最接近数学目标的方案.

b.当所有的方案都是不可行的，最优化的设计方案是最接近可行的方案而不考虑目标函数值.

1.4 优化方法

ANSYS的优化模块提供了两种优化方法：一阶分析法和子问题逼近法.这两种方法对于大多数实际问题已经足够，ANSYS还允许用户提供外部的优化算法.

1.4.1 子问题逼近法

子问题逼近法是一种先进的零阶方法，即只需要独立变量而不需要独立变量的导数.本方法中，程序用曲线拟合来建立目标函数和设计变量之间的关系.每次优化循环生成一个新的数据点，目标函数完成一次更新.实际上是逼近被求解最小值而并非目标函数.状态变量也是同样处理的，每个状态变量都生成一个逼近并在每次循环后更新.

1.4.2 一阶分析法

一阶方法同零阶方法一样，一阶方法通过对目标函数添加罚函数将问题转换为非约束的.但是，与零阶方法不同的是，一阶方法将真实的有限元结果最小化，而不是对逼近数值进行操作.一阶方法使用因变量对设计变量的偏导数.在每次迭代中，梯度计算（用最大斜度法或共轭方向法）确定搜索方向，并用线搜索法对非约束问题进行最小化.因此，每次迭代都有一系列的子迭代（其中包括搜索方向和梯度计算）组成.这就使得一次优化迭代有多次分析循环.

与零阶方法相比，一阶方法计算量大且结果精确，但是精确度高并不能保证最佳求解.一阶方法可能在不合理的设计序列上收敛.这时可能是找到了一个局部最小值，或是不存在合理设计空间.如果出现这种情况，可以使用子问题逼近法，因其可以更好地研究整个设计空间.也可以先运行随机搜索确定合理设计空间（如果存在的话），然后以合理设计序列为起点重新运行一阶方法.

1.5 优化工具

优化工具是搜索和处理设计空间的技术，也可以当作优化方法使用.ANSYS提供了单步运行法、随机搜索法、乘子评估法、扫描法、梯度法等工具［6］.

1.6 优化准则

优化准则是控制优化过程结束的条件.则在满足下面各式中任一时，则认为迭代收敛，于是迭代结束.

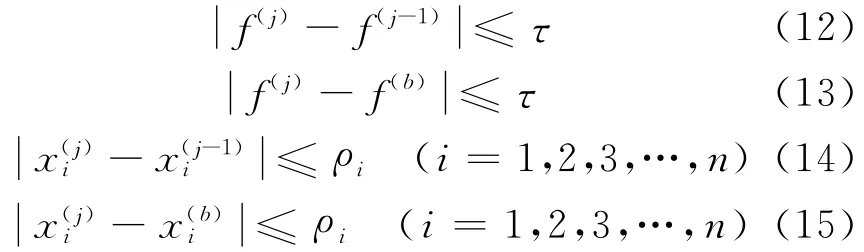
式中，τ，ρi 分别为目标函数和设计变量的允差；f（j），分别为目标函数和设计变量的当前迭代结果和上 一步 迭代结果分别为当前最优的目标函数值和相应的设计变量值.

如果式（12）～（15）都不满足，若满足以下条件时，则迭代终止.

式中，ns，Ns分别为当前的迭代步和最大的设定迭代步.

2 ANSYS有限元分析及优化设计

2.1 结构参数和计算参数

某高压容器过渡结构如图1 所示，设计压力p＝15 MPa，筒体长度H＝4 000 mm，筒体内半经R1＝1 500mm，壁厚t1＝200mm，球壳内半经R2＝1 550mm，壁 厚t2＝100 mm，弹 性 模 量E ＝200GPa，泊松比μ＝0.3.求当L1和L2为何值时，该结构的最大应力强度I最小.

2.2 有限元模型

由于模型、载荷和约束都具有对称性，可将模型简化为轴对称问题进行分析.锥形段长度L1，L2初始值分别选定为筒体延长线与封头相交和过渡段与封头相切时的数值397，390mm，筒体建模长度H应远大于边缘应力的衰减长度2.5，取1 400mm.采用自由网格形式，用四边形单元183对结构进行划分，得到有限元模型.该模型共有1 672个节点、479个单元.在球壳端面施加x 方向约束，筒体端面施加y方向约束，在容器内壁施加内压，则带边界条件和载荷的有限元模型如图2所示.

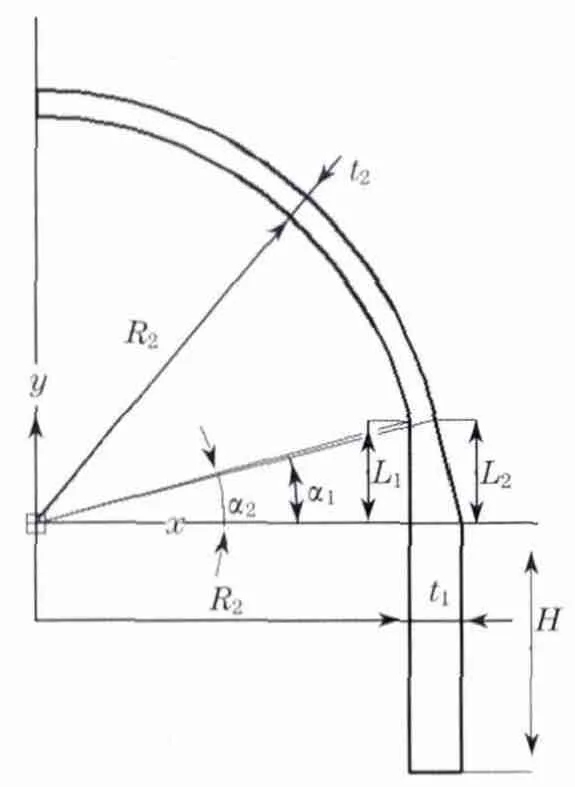
图1 过渡结构简图Fig.1 Schematic diagram of transition structure

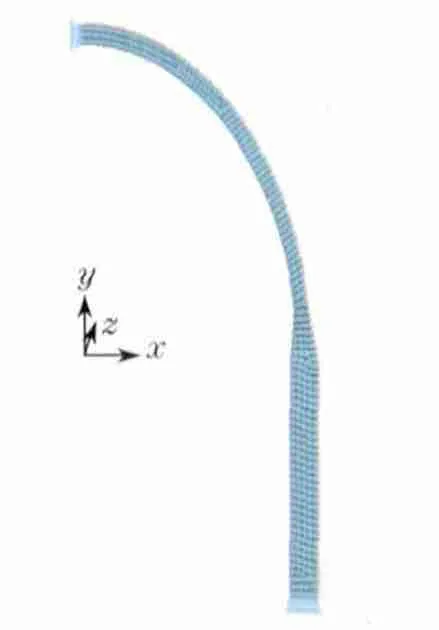
图2 带边界条件和载荷的有限元模型Fig.2 Finite element model under loads and boundary conditions

2.3 有限元分析结果

利用ANSYS后处理显示功能可得到应力强度分布云图，如图3所示（见下页）.从图上可以看出，最大应力强度I出现在球壳和过渡段的内壁面连接处，最大应力强度为192MPa.过应力强度最大点沿壁厚方向定义路径，如图4所示（见下页）.提取该路径上的应力强度分布曲线，如图5所示（见下页）.可以看出，应力强度沿着壁厚方向并非均匀分布，在连接处内表面应力强度最高，沿着壁厚向外方向应力强度逐渐下降，到外面下降到最小值，符合受压容器的应力分布规律.

2.4 优化设计的数学模型

不连续区成锥形过渡结构，容易产生应力集中.当锥形段长度L1和L2变化到某一值，必能使过渡区应力强度水平最低.因此目标函数为过渡区的最大应力强度Imax（L），设计变量选择为锥形过渡段

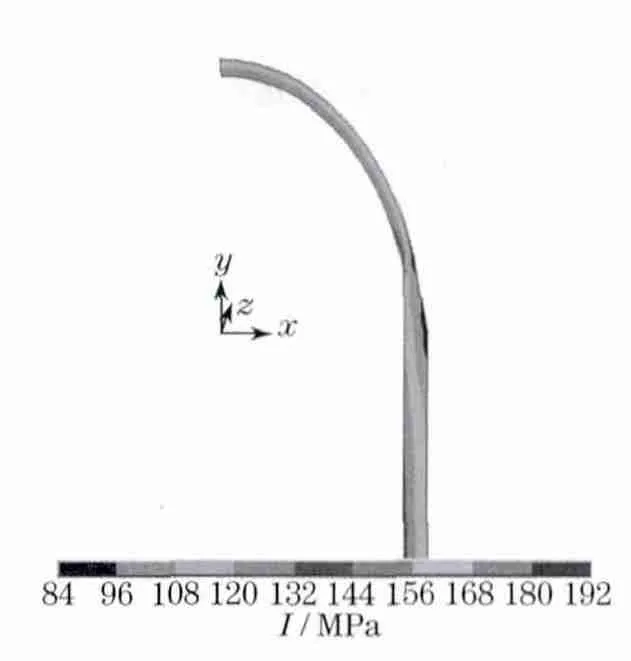
图3 应力强度云图Fig.3 Stress intensity contour

图4 路径Fig.4 Path

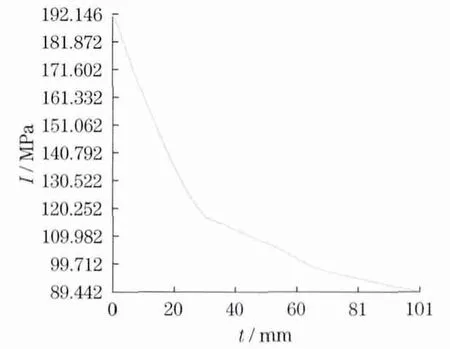
图5 应力强度分布曲线Fig.5 Distribution curve of stress intensity

长度L1和L2，根据文献［7］，有

其中，Y＝（R1＋t1）－（R2＋t2）.L1的上限值应为过渡段与封头相切时的值，则

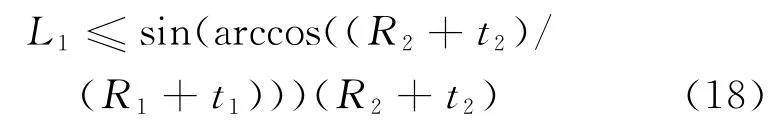
L2的上限值应为筒体内壁延长线和与封头相交时的值，则

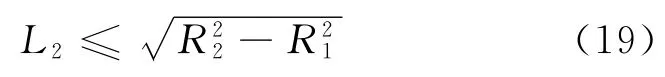
状态变量为夹角a，见图1，则a1和a2的范围为

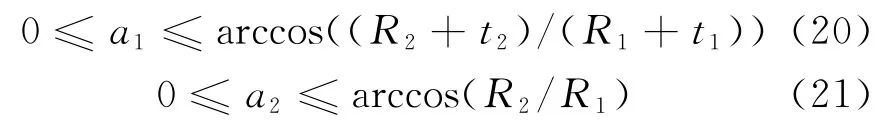
综上所述，可得优化设计的数学模型

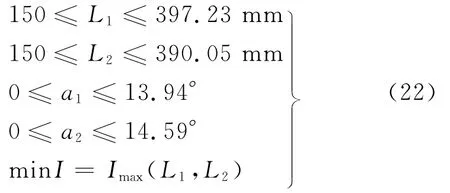
式中，Imax（L1，L2）为筒体和封头通过线性变厚段连接结构的最大当量应力强度.

3 优化设计分析结果

由于一阶分析法容易产生局部最小值，本文采用随机搜索法对压力容器过渡段进行优化设计，最大迭代次数为50次，SET43 为最优解.此时L1＝301.98mm，L2＝278.64mm，结构最大的应力强度I仅为171.75 MPa，比优化前下降了10.6%，优化效果明显；同时也可以看出相切时设计不一定是最优化的设计.目标函数随迭代次数的变化规律如图6所示，目标函数随设计变量L1和L2的变化规律如图7所示，优化后的应力强度分布云图如图8所示.从图6和图7可以看出，还存在一个次最优解，此时I＝172.05 MPa.

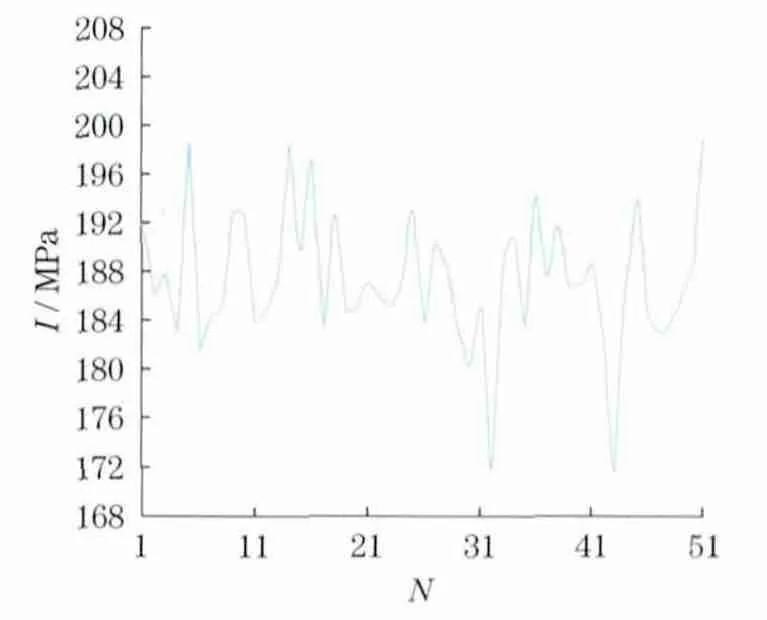
图6 目标函数随迭代次数的变化规律Fig.6 Variation of objective function with iteration times

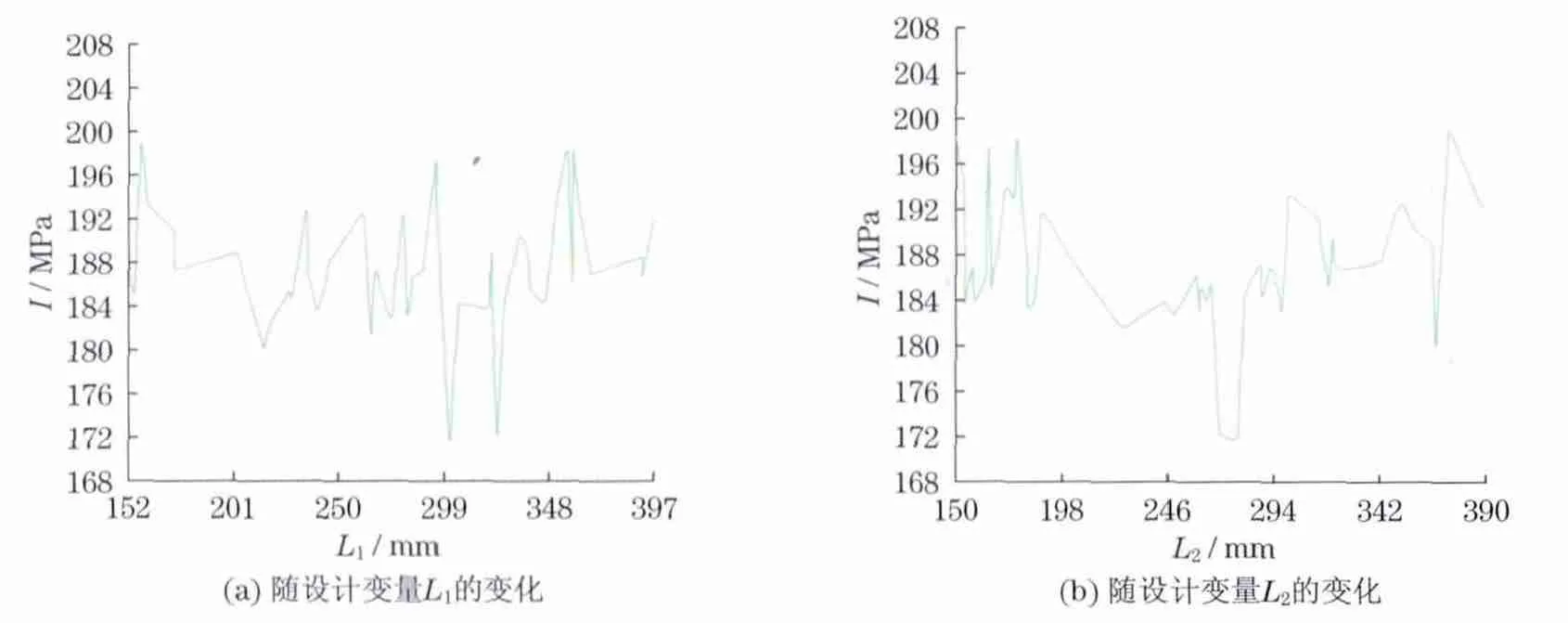
图7 目标函数随设计变量的变化规律Fig.7 Variation of objective function with design variable

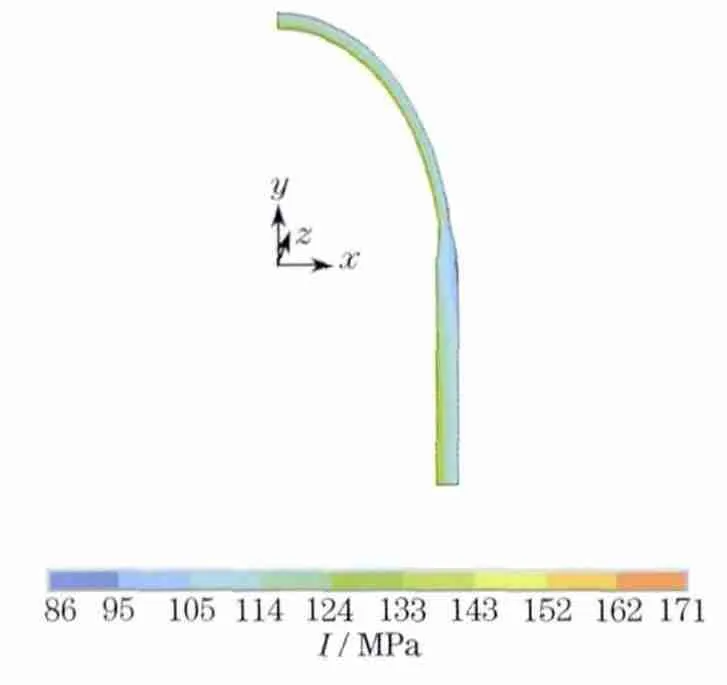
图8 优化后的应力强度分布云图Fig.8 Stress intensity contour after optimization

4 结 论

首先利用ANSYS软件对受压容器的封头和筒体过渡区进行了有限元分析，得到应力强度分布状态；结果表明，最大应力出现在过渡区与封头的内壁连接处.然后利用优化分析模块OPT 对过渡结构进行了结构优化设计，最大应力强度下降了10.6%，优化效果明显，表明局部结构优化设计对压力容器的设计起到了十分重要的作用，同时也可以观察到结构也可能同时存在几种相差不大的次最优结构.这对研究压力容器或其它结构的优化具有一定的参考价值.

［1］郑津洋，董其伍，桑芝富.过程设备设计［M］.3 版.北京：化学工业出版社，2010.

［2］张宏.压力容器的分析设计软件［J］.化工设备设计，1998，35（6）：35－36.

［3］张爱玲，蒋岚，成波.基于ANSYS 的结构优化设计方法［J］.工程结构，2009，29（3）：146－150.

［4］Zhi Y S，Wang Z R.Stress analysis of two－arc approximate ellipsoidal pressure vessel heads and parameter optimization［J］.International Journal of Pressure Vessels and Piping，1996，67（2）：199－202.

［5］Magnucki K，Szyc W，Lewiński J.Minimization of stress concentration factor in cylindrical pressure vessels with ellipsoidal heads original research article［J］.International Journal of Pressure Vessels and Piping，2002，79（12）：841－846.

［6］高要东，刘 学 杰.ANSYS 机 械 工 程 应 用 精 华50 例［M］.3版.北京：电子工业出版社，2011.

［7］中国国家标准化管理委员会.GB 150.1～150.4－2011，压力容器［S］.北京；中国标准出版社，2012.