具有强阻尼的非线性梁方程的全局吸引子＊

任永华，张建文

（太原理工大学 数学学院，山西 太原 030024）

0 引言

在非线性发展方程的领域中，系统的长时间动力学行为是由其所对应的半群的吸引子来描述的.一直以来，对系统解的吸引子的研究受到众多科技工作者的高度关注，并涌现出了大量的文献［1-12］.当函数，g′（u）有界，g（0）＝0，且时，考虑了梯度系统（1）～（3）的渐近行为［11］.对于一般抽象函数，由系统（1）～（3）定义的连续半群是点耗散的，并且系统存在整体吸引子［12］.

目前，弦方程解的吸引子理论已经得到了相当的发展，但对于梁方程的吸引子的研究文献还相对较少.本文在前人研究的基础上，考虑了齐次Dirichlet边界条件下具有强阻尼的梁方程系统在空间E＝V×H中全局吸引子的存在性.

赋予初始条件

和齐次Dirichlet边界条件

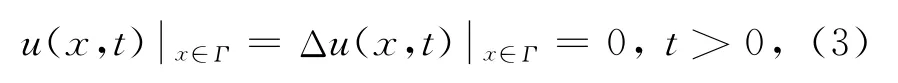
式中：γ＞0，u＝u（x，t）是关于变量x和t的Ω×R+的实值算子函数.Ω⊂Rn是具有充分光滑边界Γ的有界开集.

1 解的存在唯一性

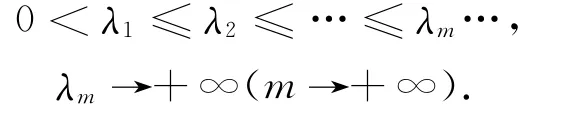
令H＝L2（Ω），V＝H20（Ω）和E＝V×H，且它们的内积和范数分别为

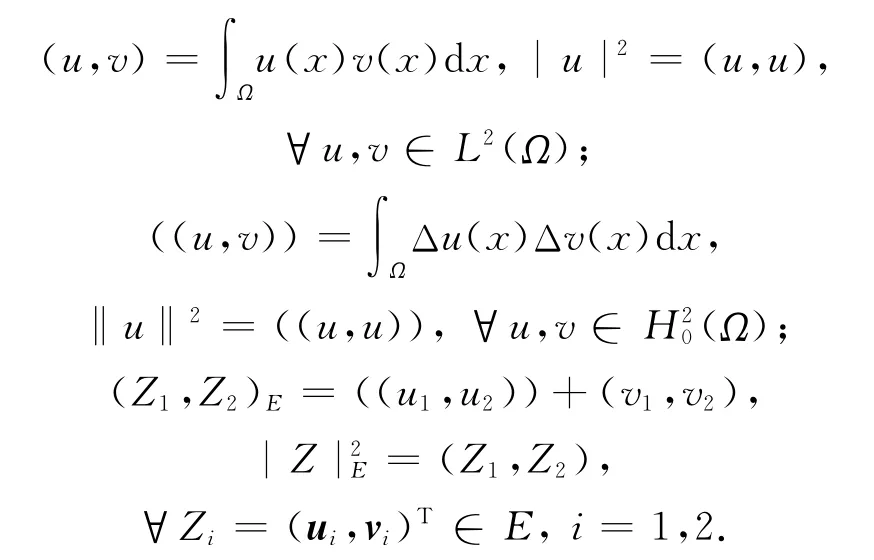
下面考虑系统（1）～（3）.为了证明解的存在性，假设函数g（u，v）满足：

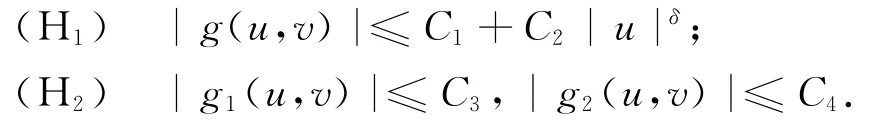
式中：∀（u，v）∈R×R，Ci为非负常数，0＜δ＜1.

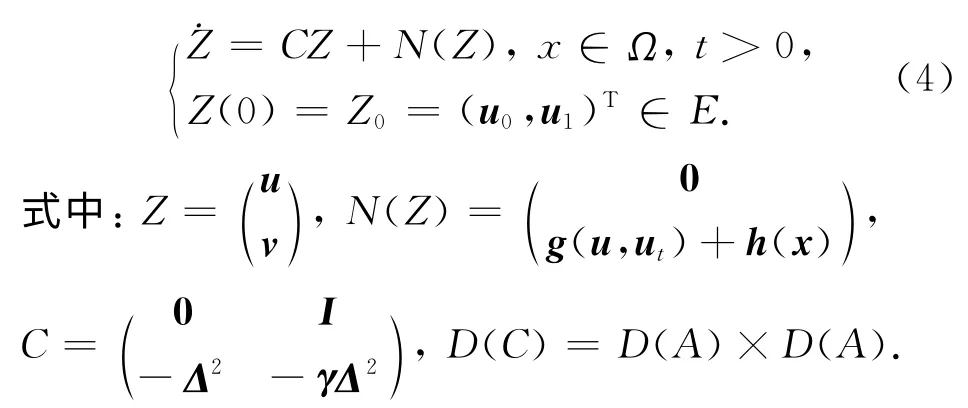
由文献［12］结合上述结论可知，半群eCt的无穷小生成元为C，又由于C是一个扇形算子，则eCt是E中生成的一个解析半群eCt.由参考文献［6］，易知N（U）在E上是全局Lipschitz 连续的.再由微分方程的解的存在唯一性理论，有定理1.

定理1 对于任意给定的Z0∈E，假设α＞0，g（u，v）满足条件（H1）～（H2），那么存在唯一函数Z（t）＝Z（t，Z0）∈C（R+，E），使得Z0＝Z（0，Z0）且Z（t）满足下面的积分方程

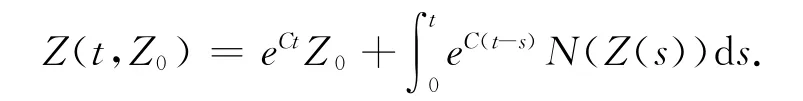
Z（t，Z0）关于t和Z0共同连续，

根据定理1 解的存在唯一性，对于任意的t≥0，引入一个E上的自治动力系统，则可以定义空间E上的一个连续半群｛S（t），t≥0｝.其中映射S（t）：Z0→Z（t，Z0），且Z（t，Z0）是系统（4）的mild 解.

2 全局吸引子的存在性

为了得到本文的主要定理，在空间E上定义加权内积和范数如下：

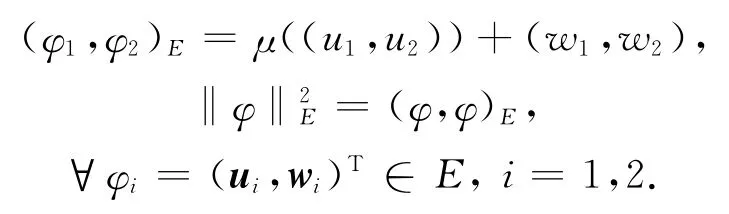
其中：

易知，函数｜·｜E等价于E中的通常范数‖·‖E.

设φ＝（u，w）T∈E，则系统（1）～（3）（或（4））可以等价地写成

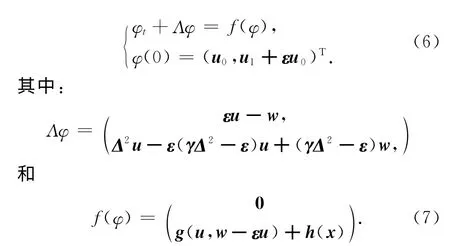
为了研究解的全局吸引子的存在性，首先介绍下面的引理：

引理1 对于∀φ＝（u，w）T，有

证明 对于∀φ＝（u，w）T，当μ＝1-εγ时，有

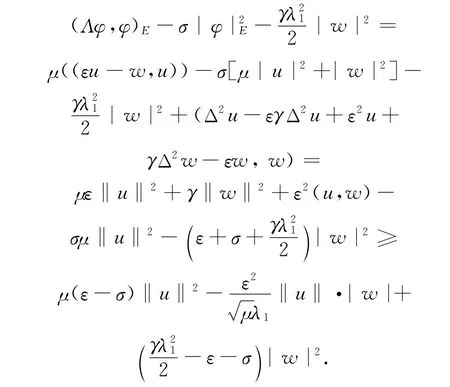
通过简单的计算可得

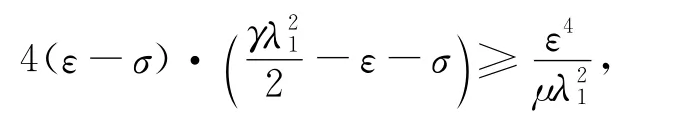
因此，引理得证.

接下来讨论空间E上半群｛S（t），t≥0｝的吸收性质.

引理2 对于∀φ＝（u，w）T，有

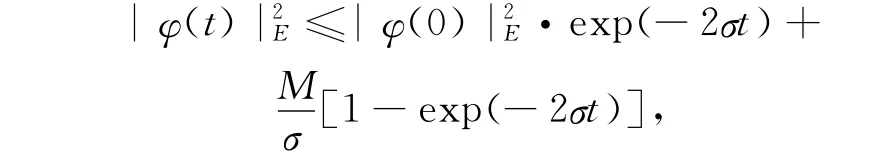
或

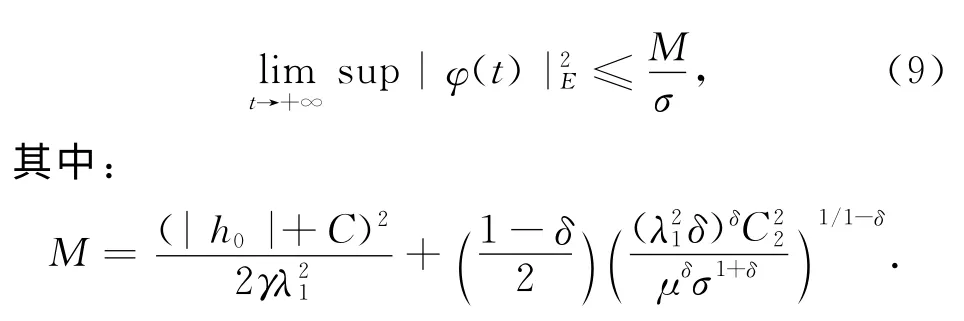
证明 ∀φ＝（u，w）T∈Ε是系统的解.

用φ在E中与问题（6）做内积（.，.）E，得

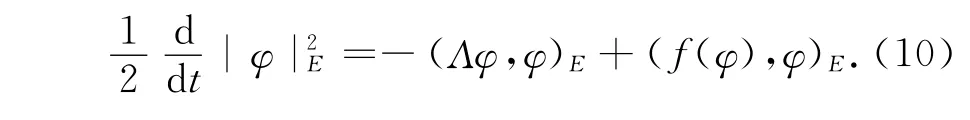
由引理1可知

由式（7）可得

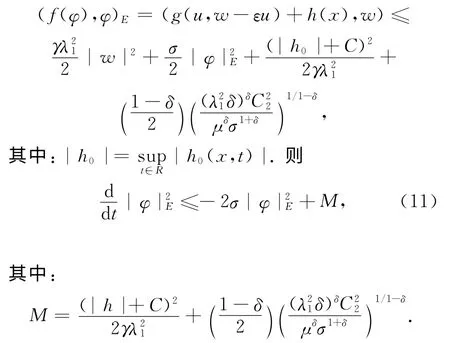
根据Gronwall不等式，可得到下列在空间（E，｜·｜E）中的吸收不等式

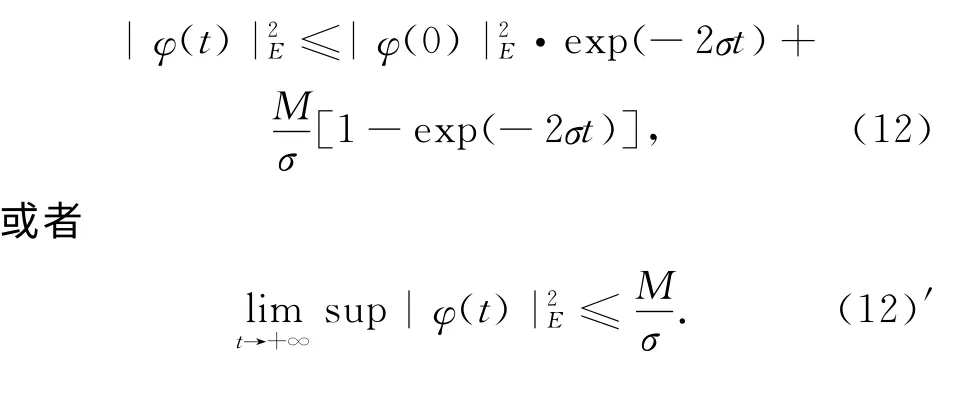
根据上述结论，可直接得出：对应于问题（1）～（3）的半群｛S（t），t≥0｝存在一致有界吸收集B0.也就是说，吸收集

是一致吸收的.因此，当t≥t1（B）时，对于E的任意有界集B，S（t）B⊆B0成立.

引理3 对应于问题（6）的半群｛S（t），t≥0｝在E中存在有界吸收集.

证明 设φ＝（u，v）T是问题（6）的解.令φ1（t）和φ2（t）是初值分别为问题（6）中φ1和φ2的两个解，且分别满足下面两个方程：

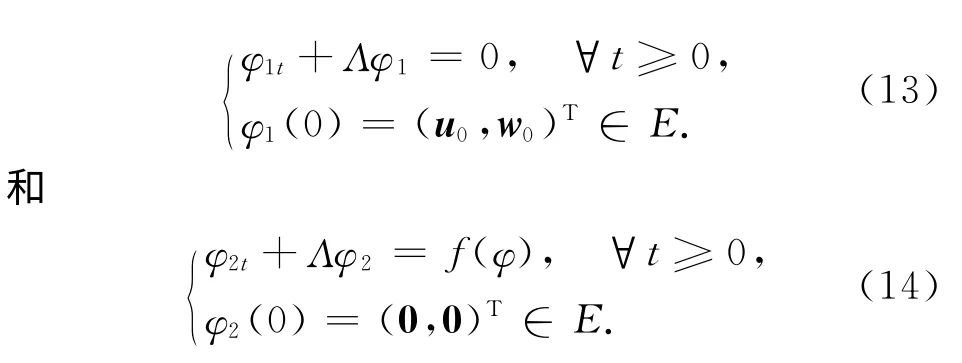
由此可得，Sε（t）＝S1（t）+S2（t）.类似于引理1和2 的证明，可知

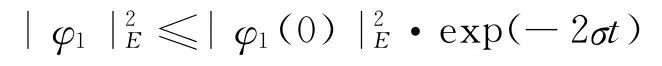
成立，因此可得S1（t）是指数衰减的.

由于φ2（0）＝（0，0）T∈D（C），用Aφ2在E中与方程（14）作内积，可得

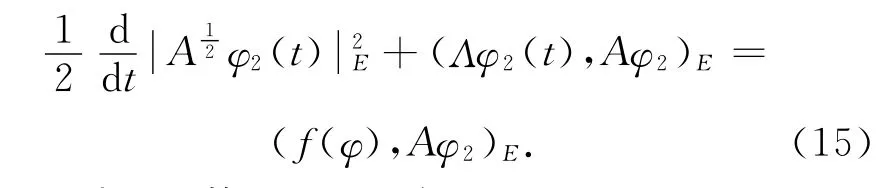
类似于引理1的证明，可得

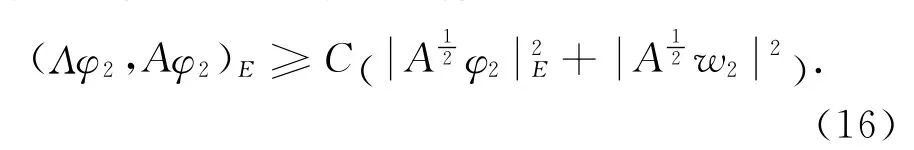
另外，通过简单的计算有

结合上述计算可得

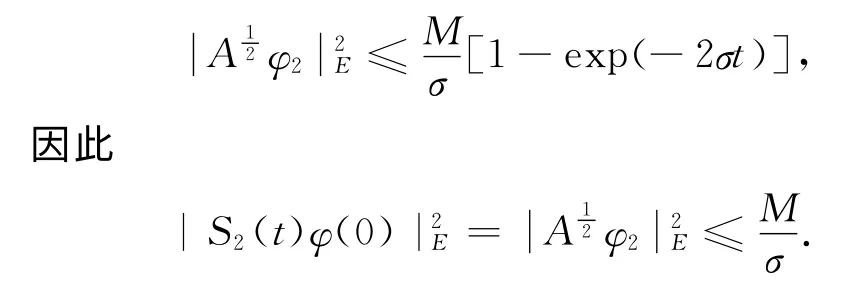
于是，当B0⊂E是一个有界集时，中的有界集.又由于D（A）×紧 嵌 入E，故是D（A）×中的紧集.结合引理2和引理3，可得下列定理.

定理2 假设α＞0，g（u，v）满足条件（H1）和（H2），则系统（1）～（3）在空间E中所定义的算子半群｛Sε（t），t≥0｝存在全局吸引子.

［1］Temam R.Infinite-Dimensional Dynamical Systems in Mechanics and Physics［M］.New York：Springer-Verlag，1988.

［2］Zhang J W，Ren Y H，Wu R H，et al.The global attractor of nonlinear thermoelastic coupled Sine-Gordon system［J］.Acta Phys.Sin.，2012，61：110404-1-5.

［3］Ren Y H.Longtime behavior of a non-autonomous beam equation［J］.Scientific Bulletin，Series A：Applied Mathematics and Physics，2013，75：135-146.

［4］Zhou S F，Fan X M.Kernel sections for non-autonomous strongly damped wave equations［J］.J.Math.Anal.Appl.，2002，275：850-869.

［5］Fan X M，Zhou S F.Kernel sections for non-autonomous strongly damped wave equations of non-degenerate Kirchhoff-type［J］.Applied Mathematics and Computation，2004，158：253-266.

［6］Jiang Y，Xie Y Q.Global attractors for a class nonlinear evolution equation［J］.Mathematical Theory and Applications，2010，30：24-28.

［7］Wang C M，Wang X，Zhong C K.Existence of global attractors for weak dissipation abstract evolution equations［J］.Pure and Applied Mathematics，2012，28：401-411.

［8］Meyries M.Global attractors in stronger norms for a class of parabolic systems with nonlinear boundary conditions［J］.Nonlinear Analysis，2012，75：2922-2935.

［9］Wakasugi Y.Small data global existence for the semilinear wave equation with space-time dependent damping［J］.J.Math.Anal.Appl.，2012，393：66-79.

［10］Pazy A.Semigroups of Linear Operator and Applications to Partial Differential Equations［M］.New York：Springer-Verlag，1983.

［11］Webb G F.Existence and asymptotic behavior for a strongly damped nonlinear wave equation［J］.Canad.J.Math.，1980，32：334-349.

［12］Massatt P.Limiting behavior for strongly damped nonlinear wave equations［J］.J.Differential Equations，1983，48：334-349.