椭圆矩形翅片管通道内流动与换热特性的数值研究＊

陈富强，阴继翔，何泽明

（太原理工大学 电气与动力工程学院，山西 太原 030024）

空冷技术的引入，很好地解决了华北地区富煤缺水的难题.发电厂空冷技术从提出到现在约有50年的历史，并在国际上有了迅速的发展，已出现单机容量686mW 的空冷机组.目前用于发电厂的空冷系统主要有三种：即直接空冷系统，表面凝气式间接空冷系统和混合式凝气间接空冷系统，其中直接空冷技术在空冷电站的应用尤为广泛［1］.直接空冷凝气器的核心元件的发展经历了三个阶段：20 世纪50年代为圆管圆翅片四排管，70年代为矩形翅片椭圆管双排管，90年代为蛇形单排管［2］.矩形翅片椭圆管换热器以其较好的流动与换热特性而倍受关注，曾有许多科技工作者对其进行过实验与数值研究，其中形成换热器通道的形状参数以及流动参数是换热器设计中需要考虑的两个主要因素.马晓茜等［3］对空气横掠椭圆管矩形翅片和圆管圆翅片的单排管进行了实验对比，结果表明：椭圆管矩形翅片比圆管圆翅片具有较优的传热和阻力性能.明廷臻等［4］对电站空冷器椭圆管矩形翅片空气侧的流动与换热特性进行了数值研究，分析了翅片间距、翅片厚度、迎面风速以及环境温度对翅片侧流体与壁面之间的表面传热系数以及流动阻力的影响.黄素逸等［5］对带有4 个扰流孔且矩形翅片尺寸参数随着椭圆管长短轴之比a／b的改变而变化的矩形翅片椭圆管进行了强制对流换热研究，分析了a／b不同时其翅片间距对放热的影响，并根据实验结果拟合出了相应的实验关联式.结果表明：用椭圆管矩形翅片做散热元件，且当a／b＝2.75，lgRe＝4.8时，其放热系数比圆管矩形翅片提高了5%；在同样迎风面或体积下，可布置更多的换热面.闵敬春等［6］给出了椭圆管直翅片二维导热效率的计算方法，利用扇形法计算了长短轴比范围为1～5的椭圆管直翅片换热器在不同工况下的翅片效率，并与等周长法和等面积法的计算结果进行了比较.结果表明：与扇形法计算的效率相比，等周长法的结果偏高，等面积法的结果偏低.总之，对矩形翅片椭圆管换热器的研究多数集中于翅片间距、管排数、翅片厚度、椭圆管偏心距离等［7-10］几何参数对换热及流动的影响分析，而且就目前的测试手段，实验研究难以确定翅片表面的温度，均在翅片为恒壁温的假设条件下完成.而对于椭圆基管周长恒定，椭圆管长短轴尺寸变化对翅片管换热及流动特性的分析研究以及三维流动与换热时翅片效率的研究却鲜有报道.基于上述原因，本文运用等周长法建立了椭圆管长短轴比值K不同时的矩形翅片椭圆管三维几何模型，利用Fluent商用软件对椭圆矩形翅片管通道内层流流动与换热特性进行了数值模拟，考察分析了K值及Re数对流动阻力、换热特性、翅片效率及综合性能的影响，为椭圆矩形翅片管长短轴的选择和优化设计提供了理论依据.

1 物理问题及数值方法

1.1 几何模型

根据翅片管管外空气流动和换热在沿管长方向具有周期性的特点，选取一个周期单元作为计算区域；另外，因翅片沿主流方向具有对称性，故取翅片的一半进行分析研究.横向尺寸由翅片和管子中心纵剖面界定，高度由翅片厚度中分面及翅片间距的一半来界定［11］.本文固定不同K值的管壁周长为222.8mm，即每种管型具有相同的换热表面积，不同长短轴之比的椭圆管尺寸见表1.矩形翅片尺寸保持不变，其宽度W＝49mm，长度L＝119mm，翅片间距s＝4.0mm，翅片厚度δ＝0.35mm.

表1 椭圆管尺寸Tab.1 Elliptical tube size

为了保证计算的稳定性以及满足进出口边界条件设置的需求，将进出口区分别延长2倍、6倍椭圆管当量直径的长度，这样可避免出口边界的回流对计算结果的影响.图1 给出了计算区域示意图，为节省空间，此处没有按实际尺寸绘制.

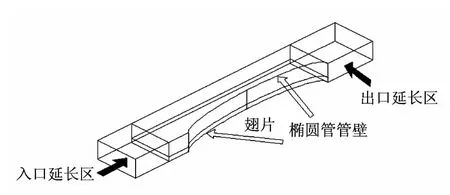
图1 计算区域示意图Fig.1 Schematic diagram of calculation domain

1.2 流动状态的确定

翅片管结构可视为平板穿管的槽道内流动结构（即属于内部流动问题），流动由层流向湍流转变的临界雷诺数在2 300 左右［12］，本文选取的迎面流速范围为1～4.2 m／s，对应的Re均小于2 300，属于层流流动.雷诺数Re及当量直径De的定义如下：

式中：A为入口横截面面积，m2；P为湿周周长，m；uin为入口空气流速，m／s.

1.3 控制方程

本文在进行数值模拟时做了如下假设：①流体为不可压缩流体；②流动为稳态、层流；③流体在壁面处无滑移；④翅管、翅片材料物性参数为常数；⑤不考虑自然对流和辐射换热的影响.流动与换热遵循的微分方程为

式中：φ＝1；u，v，w，T分别代表连续方程、动量方程、能量方程；扩散系数Γ和源项Sφ随变量φ的不同而具有不同的含义.

1.4 边界条件

为了获得物理问题的唯一解，需要定义相应的边界条件.进口为速度边界条件；流体入口温度设为293K；出口采用局部单向化条件；椭圆管壁温度恒定（373K）；翅片表面和进出口端面设为耦合边界条件，其温度需要通过计算确定，由翅片导热及其与空气的对流耦合求解而得；翅片边缘采用绝热边界条件；其余边界均取对称性边界条件.

1.5 数值计算方法

压力与速度的耦合选取SIMPLE 算法完成；对流项的离散采用一阶迎风格式；计算方程组残差收敛条件为：连续性方程为10-4，动量方程与能量方程为10-6.对计算区域采用六面体结构化网格进行划分，为有效求解近壁处较大的速度和温度梯度将壁面附近网格加密，计算区域局部网格如图2 所示.

图2 计算区域局部网格Fig.2 Local grid for calculation domain

2 计算所用参数的定义

1）椭圆管周长

式中：a，b分别为椭圆管长轴半径及短轴半径，m.

2）努塞尔特数

3）阻力系数

式中：uin为入口空气流速，m／s；ΔP为翅片段空气的压降，Pa；L为翅片纵向长度，m.

4）换热因子

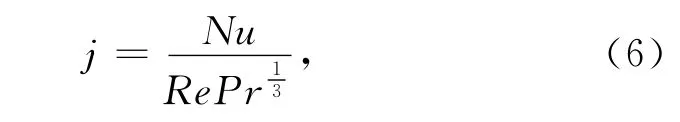
式中：Pr为普朗特数，

3 算法考核

为了验证本文计算方法的可靠性，对K＝5的椭圆矩形翅片管模型进行了模拟计算.图3 为计算所得翅片管空气侧的平均换热系数与文献［4，13］提供的数据的比较.根据几何结构的周期性和对称性，本文计算时选取图1 所示的单元通道作为计算区域，为保证计算的稳定性和可靠性，对进出口处分别进行了适当延长.而文献［4］中提供的数据是对500mm 长的椭圆翅片管空气侧的翅片通道进行数值模拟的结果，导致本文计算结果和文献值存在一定的误差.文献［4］用实验［13］的数据验证了其算法的合理性，限于参考文献中给定的条件不充分，其计算进行了适当的假设，同样使得计算结果［4］与实验结果［13］存在一定误差.本文模拟值与文献［4］和实验［13］各点的相对误差在5%～20% 之间，充分说明了本文算法的有效性和可靠性.

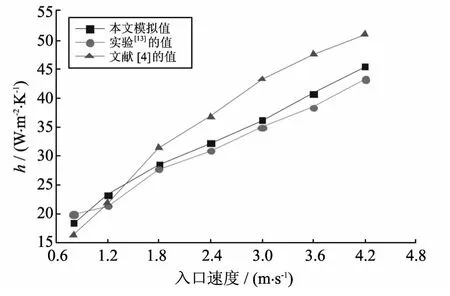
图3 实验结果与数值计算结果的对比Fig.3 Comparison of experimental results and numerical results

4 结果分析与讨论

4.1 翅片表面温度场和局部努塞尔特数的分布

图4为不同雷诺数以及不同长短轴比值K时翅片表面的温度分布.随着雷诺数的增大，空气的扰流增加，翅片表面与周围流体的对流换热增强，使得翅片得到有效冷却，翅片表面的温度明显下降.在基管前端的迎风面处，等温线密集，温度梯度变化相对较大，换热较强.在椭圆管后始终存在着尾流区，由于在尾流区中被加热的热空气温度较高，从而可能会出现翅片被加热的负热流密度现象.负热流密度区域的存在使得翅片的强化换热的作用减弱.

图4 不同雷诺数及管型下翅片表面温度分布Fig.4 Distributions of isothermal on fin surface for different Reand tube type

图5 为不同雷诺数以及不同K值时翅片表面局部努赛尔特数的分布.由图5 可知，翅片前端迎风面的Nu较大，下游方向的Nu值逐渐减小.在椭圆管后端背风面存在尾流区，阻碍了空气流动换热，努赛尔特数最小，换热能力最弱.当Re＝1 350 时，随着K值的增加，椭圆管后端形成尾流区处的范围减小，所以翅片后端及基管附近流体的扰动程度较弱，使得此处的Nu数减小.

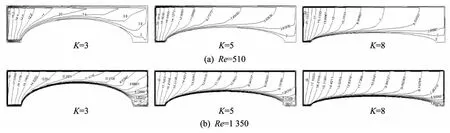
图5 翅片表面局部努赛尔特数分布图Fig.5 Local Nudistributions on fin surface

4.2 相邻翅片中心截面的流线分布

相邻翅片中心截面上的流线分布如图6 所示.在流场中，当流动方向与椭圆管长轴平行时，椭圆管的流线型较好，气流与管的分离点后移，减少了管后的漩涡区，使流体阻力减小.椭圆管长短半轴之比越大，管道截面形状变得细长，使得压降减小，流体和管的分离点越向后，漩涡区越小，流阻也越小.

图6 不同雷诺数及管型下的流线分布Fig.6 Streamline distribution of different Reand tube type

4.3 翅片管外空气侧换热特性

图7 为椭圆管壁和翅片表面平均Nu数随Re数以及K值变化的关系曲线.当K一定时，Nu数随着Re数的增加而增加，因为随着Re数的增大，翅片表面的边界层厚度减薄，翅片表面平均温度降低，平均对流传热增加，对流传热效果得到增强.当Re数一定时，随着椭圆基管长短半轴的比值K的增加，翅片与管壁的平均Nu数逐渐减小，其减小的幅度减缓.K＝10的翅片管Nu数比K＝3的翅片管减小了约4.66%～9.83%.

图7 Re，K的变化对Nu数的影响Fig.7 Variations of Nuwith Reand K

4.4 翅片管外空气侧阻力特性

图8 是K取不同值时，翅片管外空气侧阻力系数f随Re数变化的规律.由图8可知，当K值一定时，阻力系数f随Re数的增大而减小；对于给定的Re数，随K值的增加，阻力系数减小，当K＝10时，阻力系数最小，这是由于K值大的管形具有较好的流线型所致.K＝10的翅片管外空气侧阻力系数比K＝3 的翅片管减小了约51.67%～56.6%.

图8 Re，K变化对阻力系数f的影响Fig.8 Variations of drag coefficient fwith Reand K

4.5 翅片效率的分析

翅片效率是衡量翅片散热有效程度的指标，其定义为：实际散热量与假设整个翅片表面处于翅片根部温度下的散热量之比［14］.对于同种金属材料制成的翅片，在换热条件相同，材料耗费也大体相同的条件下，翅片效率是评价翅片几何形状及尺寸设计是否合理的标准之一.显然，翅片效率越高，散热效果越理想，几何形状及尺寸就设计得越合理［15］，图9 反映了翅片效率与Re及K值的关系，由图可见，随着Re数的增大，翅片效率下降，但下降的幅度逐渐减缓；当Re数一定时，随着K值的增大，翅片效率减小，在K＝3时翅片的效率最大.从图4 可以看出，翅片表面的平均温度随着K值的增大而变小，由翅片效率的定义可知，平均温度越低，效率越低，即比值K越大，翅片效率越低，图4 对上述结论给予了充分的支撑.

图9 Re，K的变化对翅片效率的影响Fig.9 Variations of fin efficiency with Reand K

4.6 综合评价性能

有多种指标用于评价紧凑式换热器的综合性能，其中面积性能系数j／f多用于评判不同的结构参数对换热及流动阻力综合性能的影响.在操作条件一定的情况下，j／f与流体流动的迎风面积Ac成反比.j／f越大，所需的迎风面积越小，即在相同的体积内可布置更多的换热面，换热量增加；若换热量一定时，可使换热器体积、面积减小，紧凑度提高，意味着扩展面（肋片）效率较高.图10给出了综合性能参数j／f随Re数的变化关系，当K＝3 时，综合性能最差；当K＝10时，综合性能最好.

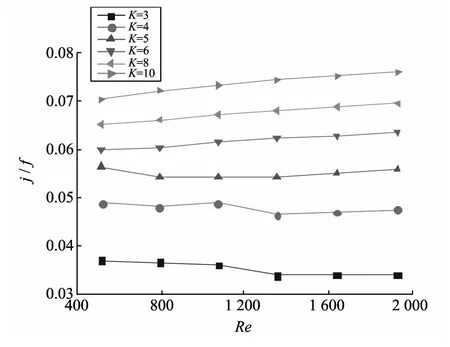
图10 Re，K变化对综合性能参数j／f的影响Fig.10 Variations of performance parameters of j／fwith Reand K

5 结论

1）当椭圆管长短轴之比固定时，就换热特性而言，随着Re数的增加，Nu数增加；当Re一定时，随着K值的增大，Nu数减小，K＝10的翅片管Nu数比K＝3 的翅片管减小了约4.66%～9.83%.

2）当椭圆管长短轴之比固定时，就阻力特性而言，随着Re数的增加，阻力系数减小；当Re一定时，随着K值的增大，f呈减小的趋势，K＝10的翅片管外空气侧阻力系数比K＝3的翅片管减小了约51.67%～56.6%.

3）当椭圆管长短轴之比固定时，就翅片效率而言，随着Re数以及K值的增大，翅片效率减小.

4）在椭圆管等周长的情况下，随着K值的增加，综合性能参数j／f增大，K＝10的管型综合性能最优.

［1］邱丽霞，郝艳红，李润林，等.直接空冷汽轮机及其热力系统［M］.北京：中国电力出版社，2006.

［2］马义伟.发电厂空冷技术的现状和进展［J］.电力设备，2006，7（3）：5-7.Ma Yiwei.Current status and progress of power plant air cooling technology［J］.Electrical Equipment，2006，7（3）：5-7.（in Chinese）

［3］马晓茜，梁淑华.空气横掠二种翅片管冷凝元件的对比实验［J］.电站辅机，1997（3）：13-16.Ma Xiaoqian，Liang Shuhua.Comparison of two kinds of finned tube condensing element air across flow［J］.Power Station Auxiliary Equipment，1997（3）：13-16.（in Chinese）

［4］明廷臻，党艳辉，刘伟，等.椭圆管矩形翅片空冷器流体流动与传热特性数值分析［J］.化工学报，2009，60（6）：1380-1384.Ming Tingzhen，Dang Yanhui，Liu Wei，et al.Numerical analysis of fluid flow and heat transfer characteristics on elliptical tube with rectangular fins of air cooler［J］.CIESC Journal，2009，60（6）：1380-1384.（in Chinese）

［5］杨金宝，黄素逸.横掠椭圆翅片管的放热［J］.流体工程，1987（4）：56-58.Yang Jinbao，Huang Suyi.Heat-transfer of air crossing across elliptic finned tube［J］.Fluid Engineering，1987（4）：56-58.（in Chinese）

［6］闵敬春，陶涛，彭晓峰.椭圆管直翅片换热器翅片效率的计算［J］.工程热物理学报，2001，22（4）：473-476.Min Jingchun，Tao Tao，Peng Xiaofeng.Calculation of fin efficiency of an elliptical finned tube heat exchanger［J］.Journal of Engineering Thermo-physics，2001，22（4）：473-476.（in Chinese）

［7］史佑吉，高伟桐，吴振亚，等.矩形翅片椭圆管传热及阻力性能的试验研究［J］.电机工程学报，1984，4（1）：53-61.Shi Youji，Gao Weitong，Wu Zhenya，et al.Experiments on heat transfer and pressure drop of air flowing across elliptical tube banks with square fins［J］.Journal of Electrical Engineering，1984，4（1）：53-61.（in Chinese）

［8］丁永航，李永光，汪军，等.空气横掠矩形翅片椭圆管束换热规律的数值研究［J］.能源研究与信息，2006，22（3）：159-164.Ding Yonghang，Li Yongguang，Wang Jun，et al.Numerical study on heat transfer of air across rectangular fins in the elliptic-tube heat exchanger［J］.Energy Research and Information，2006，22（3）：159-164.（in Chinese）

［9］冯丽丽，杜小泽，杨勇平，等.椭圆管矩形翅片间空气流动的扰流特征［J］.工程热物理学报，2011，32（1）：119-122.Feng Lili，Du Xiaoze，Yang Yongping，et al.Characteristics of air flow around elliptical tubes with rectan-gular fins［J］.Journal of Engineering Thermophysics，2011，32（1）：119-122.（in Chinese）

［10］党艳辉.直接空冷系统异型管的数值模拟［D］.武汉：华中科技大学，2009.

［11］杨建蒙，王钊，马荣荣.矩形翅片椭圆管气侧换热特性数值研究［J］.计算机科学，2011，38（7A）：59-61.Yang Jianmeng，Wang Zhao，Ma Rongrong.Numerical study on air-side flow and heat transfer characteristics for rectangular-finned elliptical tube［J］.Computer Science，2011，38（7A）：59-61.（in Chinese）

［12］Bilir L，Ilken Z，Erek A.Numerical optimization of a fin-tube gas to liquid heat exchanger［J］.International Journal of Thermal Sciences，2012，52：59-72.

［13］冯丽丽.大型电站空冷凝汽器传热特性实验研究［D］.北京：华北电力大学，2006.

［14］杨世铭，陶文铨.传热学［M］.第4版.北京：高等教育出版社，1998：62-63.

［15］张艳霞，张红，陶汉中.基于场协同理论的管翅式换热器翅片效率的数值模拟研究［J］.建筑科学，2011，27（10）：98-101.Zhang Yanxia，Zhang Hong，Tao Hanzhong.Numerical simulation on fin efficiency of tube-and-fin heat exchanger based on field synergy principle［J］.Building Science，2011，27（10）：98-101.（in Chinese）