一个带有时滞的肺结核模型的稳定性

王海霞，蒋里强，王桂花

（1.郑州师范学院 数学与统计学院，河南 郑州 450044；2.防空兵学院 基础部，河南 郑州 450052）

0 引言

直到最近几年，肺结核还是世界上许多地方引起死亡的主要原因.众所周知，一个人随时都会染上结核病.这就是说，通过偶然接触一个染病者，或者是通过接触一个结核病患者的其他家庭成员是都会染上的.据报道，每年大概有800万人会染上结核病，而且这些人每人每年仅仅通过呼吸又可以传染10～15 人.因此，研究结核病的控制与传染具有重大意义.

本文提出并讨论了两个结核病传染的数学模型：一个常微分方程模型；然后引入一个离散时滞来描述一个易感者从感染到真正成为一个结核患者的时间（即潜伏期），从而得到了一个带有离散时滞的离散时滞模型.各种类型的时滞已被众多学者引入到生物模型中（［1-6］）.本文通过分析时滞模型的超越特征方程，得到了染病平衡点稳定的条件，它只和相关参数有关，而与时滞的具体大小无关.

1 常微分方程模型

受文献［7］中常微分方程模型的启发，采用双线性发生率，提出以下常微分方程模型：

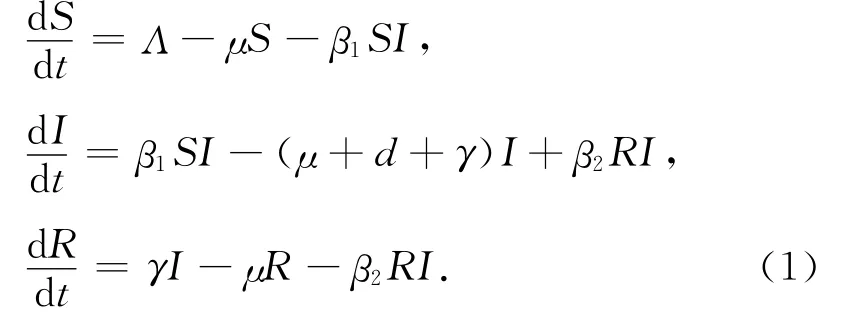
式中：Λ代表人口输入率；μ代表自然死亡率；d代表由结核病引起的死亡率.β1，β2是有效传染率；γ代表治愈率.假设所有参数均非负并且不失一般性，并假设β1≥β2.

注意到，

因此总人口N（N＝S+I+R）会随着时间的变化而变化.在无病的情况下，总人口N（t）收敛于平衡点.从式（2）可知，因此在可行域

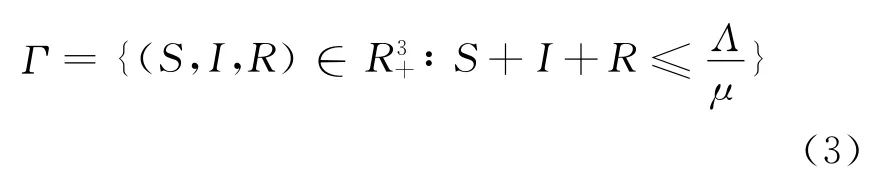
中来讨论模型（1），可以证明这正是关于（1）的正不变区域.记∂Γ和分别代表区别Γ的边界和内部.定义其中ω＝μ+d+γ.R0代表在一个大小为的完全易感人群中一个结核病患者传染易感者的平均数量，通常被称为基本再生数（［8］）.

模型（1）平衡点满足方程

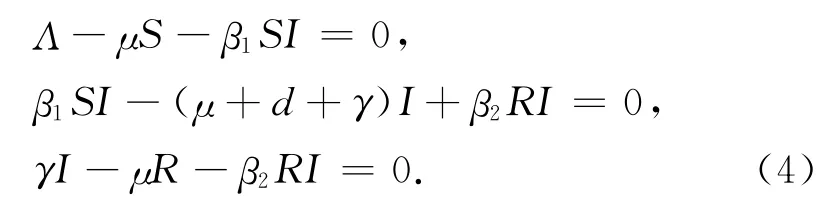
在无病的（I＝0）情况下，解方程（4），得模型的唯一的无病平衡点疾病可能持续存在（I≠0）的情况下对应于模型的地方病平衡点.考虑到平衡点（当存在时）不能被显式表示，本文将在模型参数满足某些特定条件时讨论它们的存在性.注意到方程（4）中第1和第3个方程，有又I≠0，将它们带入方程（4）中第2个方程，即

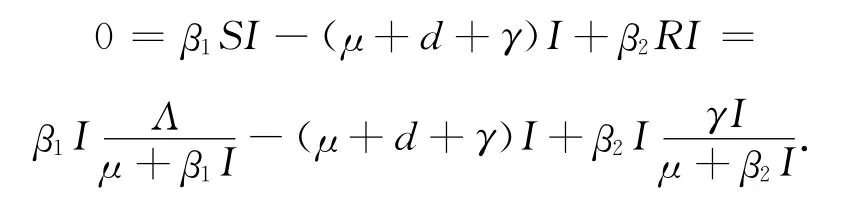
通过一个复杂的计算，得到一个二次方程

假设R0≤1，显然有C≥0，B＞0，从而Q（I）没有正根.也就是说，模型没有地方病平衡点.假设R0＞1，C＜0，此时Q（I）有两个实根，一正一负.因此模型有唯一的地方病平衡点

由上面的分析可以知道，如果R0≤1，则E0是Γ内唯一的平衡点；如果R0＞1，则在˙Γ内有唯一的地方病平衡点.其中而是二次方程Q（I）的正根.

首先考虑无病平衡点E0.模型（1）的雅可比矩阵为

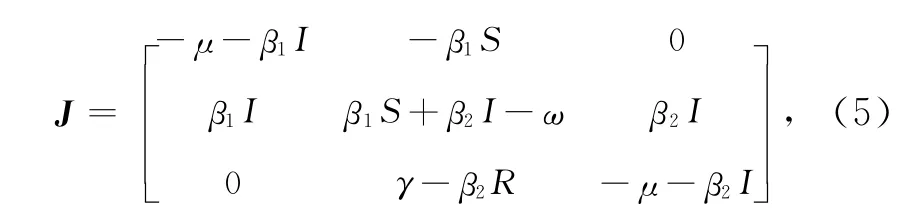
从而模型（1）在E0处的雅可比矩阵为

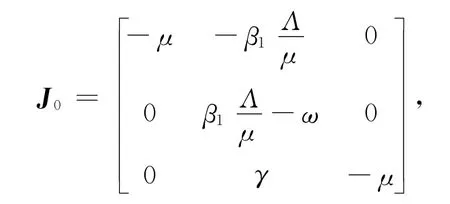
定理1 如果R0＜1，则无病平衡点E0是局部渐近稳定的；如果R0＞1，则无病平衡点E0不稳定.

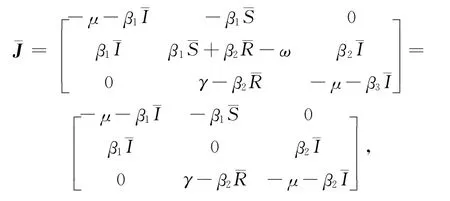
相应的特征方程为

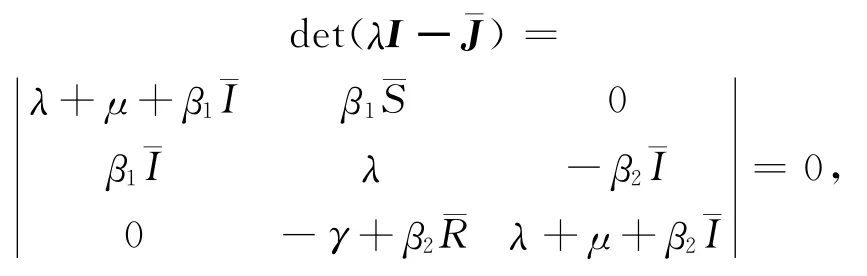
也就是

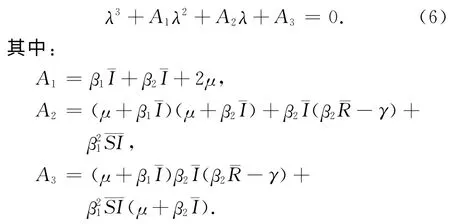
由Routh-Hurwitz判别准则可得到稳定性条件A1＞0，A3＞0和B1＝A1A2-A3＞0.注意到，对所有参数均有A1＞0.

由上，就有

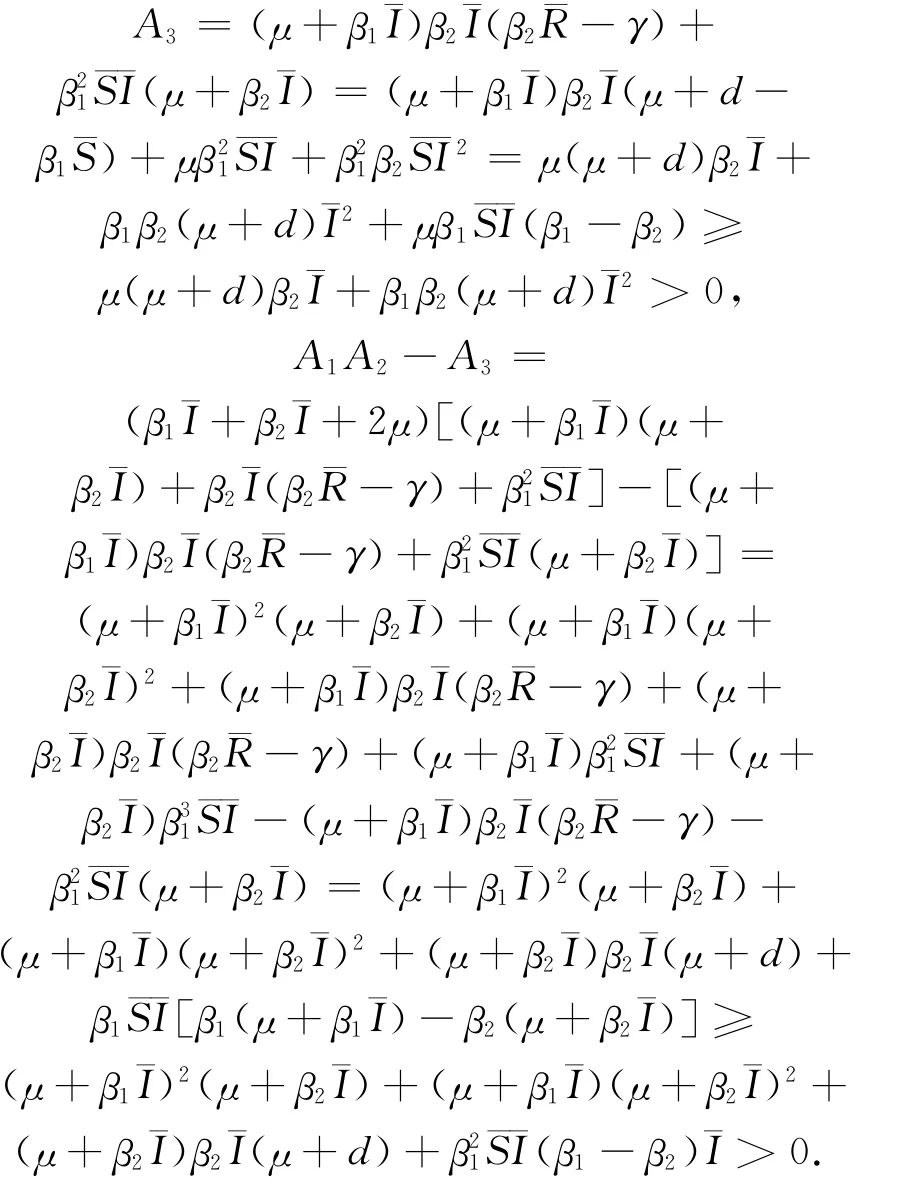
因此，当R0＞1时，地方病平衡点是局部渐近稳定的.综上分析有以下定理：

定理2 如果R0＞1，则地方病平衡点是局部渐近稳定的.

2 时滞模型

在模型（1）中引入一个离散时滞，代表潜伏期，模型如下：

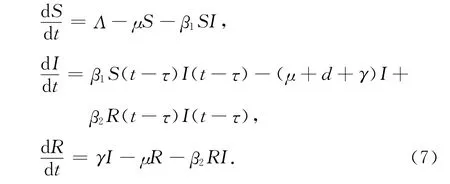
满足初始条件S（θ）＝S0，I（θ）＝0，R（θ）＝R0，θ∈［-τ，0］.这里除了τ代表潜伏期的长度即天数外，其他参数均与模型（1）中的相同.同样，又找到了一个无病平衡点和一个地方病平衡点，其中与第2部分中的一样.既然当τ＝0 且R0＞1 时无病平衡点E0是不稳定的，引入时滞也不会改变其不稳定性，因此当R0＞1时，E0不稳定，而R0＞1也正是地方病平衡点存在的条件.

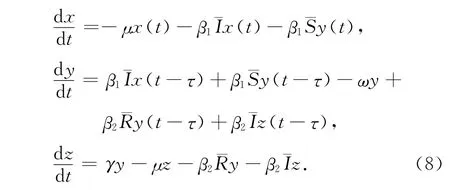
以矩阵的形式表示系统（8），即

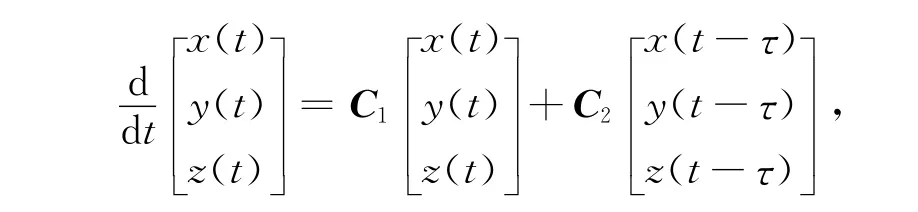
这里C1和C2是3 阶矩阵，

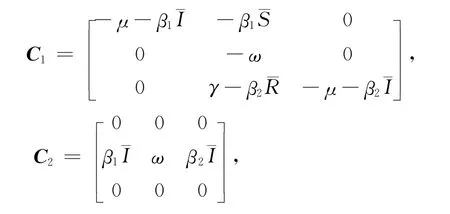
人们知道，当相应特征方程（9）的所有特征根均具有负实部时，平衡点是渐近稳定的［9］.然而，与常微分方程模型的特征方程（6）相比，方程（9）更难以处理.首先，它是一个超越方程，有无穷多个特征根；其次，由于它是超越方程，经典的Routh-Hurwitz判别准则对它将不再适用；再者，尽管也有一些常规的方法［4］可以用来确定超越特征方程的特征根何时均具有负实部，但用这样一个常规的方法来处理这个特定的超越方程也是相当复杂的［10］.

为此，本文将分析性地研究超越特征方程（9）的根的分布.回想一下常微分方程模型（1），当R0＞1时地方病平衡点是稳定的.本文的出发点是假设常微分方程（1）的地方病平衡点是稳定的，然后当导出保证时滞方程（7）仍然稳定时，其中参数满足的条件.为此，考虑τ＝0时的方程（9），也就是方程（6），并且方程（6）的所有特征根均具有负实部.由Rouché′s 定理［11］以及关于τ的连续性，超越方程（9）具有正实部的特征根当且仅当它具有纯虚根.将确定如果方程（9）具有纯虚根，从中将会找到其所有特征根均具有负实部的条件.

记方程（9）的特征根λ＝η（τ）+iξ（τ）（ξ＞0），其中η（τ）和ξ（τ）依赖于时滞τ.既然常微分方程模型的平衡点¯E是稳定的，因此当τ＝0 时η（0）＜0.由连续性知，当τ＞0 且足够小时，仍然有η（0）＜0 并且仍是稳定的.如果对某些τ0＞0使η（τ0）＝0，这时λ＝iξ（τ0）便是方程（9）的纯虚根.换言之，如果这样的ξ（τ0）不存在，也就是说如果对所有时滞，特征方程（9）都没有纯虚根，那么地方病平衡点始终是稳定的.本文将证明对特征方程（9）来说确实是这样的.

显然，如果iξ（ξ＞0）是方程（9）的一个根，当且仅当

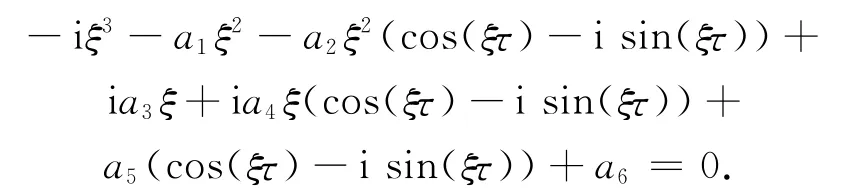
分离其实部和虚部，有

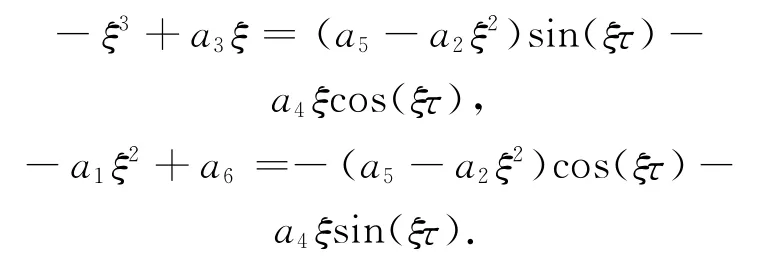
将方程两边平方再相加，得

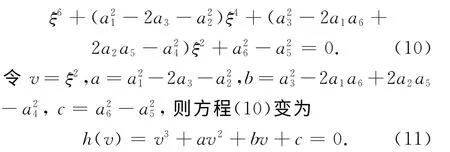
注意到，

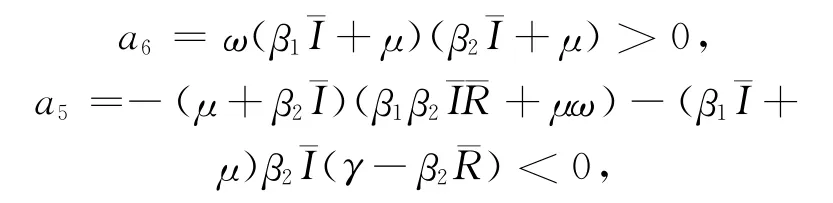
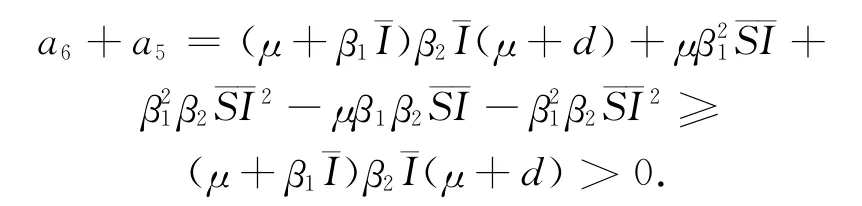
事实上，注意到对所有参数都有

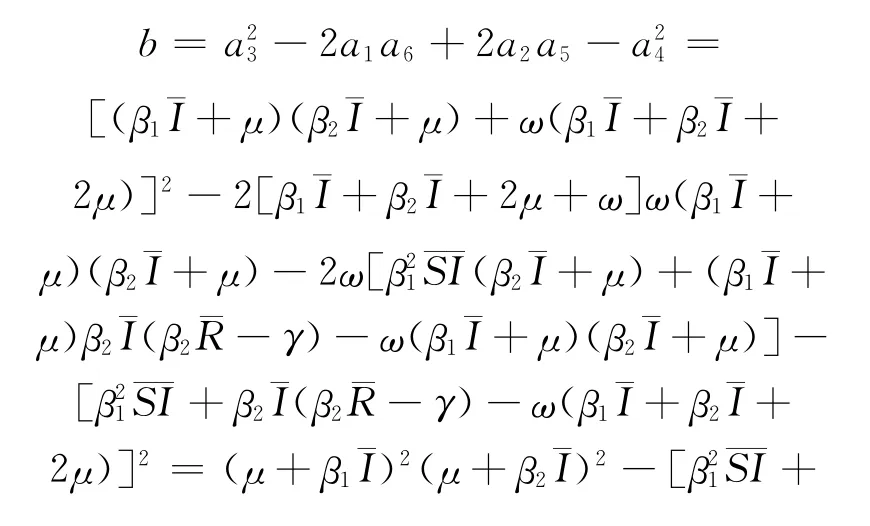
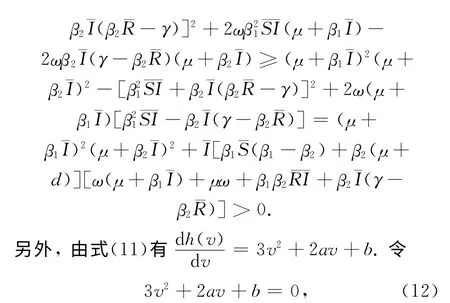
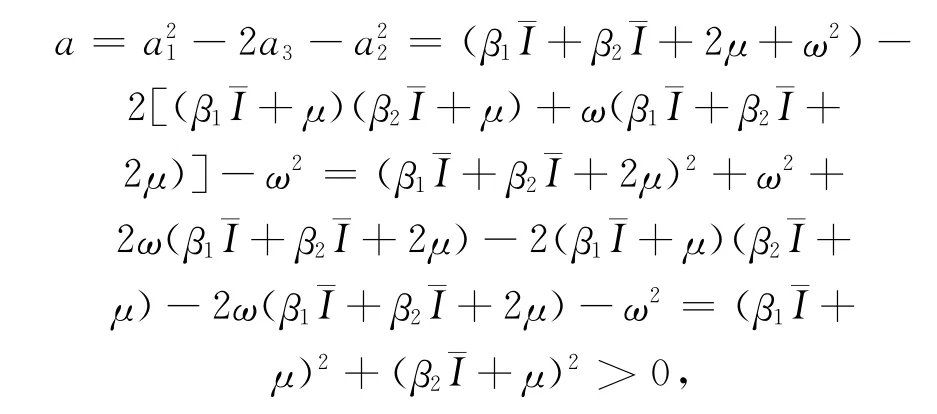
因此b＞0，a＞0，并且a2-3b＜a2.也就是说所以v1和v2均不是正的，因此方程（12）没有正根.又h（0）＝c＞0，从而方程（11）没有正根.

上面的断言意味着不存在这样的ξ使得iξ是特征方程（9）的特征根.所以，特征方程（9）的所有特征根的实部对所有时滞τ≥0 都是负的.综上分析，有如下定理：

定理3 如果R0＞1，则时滞模型（7）的地方病平衡点是绝对稳定的.这就是说，对所有的τ≥0，对所有时滞都是渐近稳定的.

正如人们所知，定理3 表示如果参数满足R0＞1，也就是说只要存在，时滞模型（7）的地方病平衡点对所有时滞都是近稳定的，也即与时滞无关.

3 结束语

提出并讨论了两个肺结核传染病的数学模型：一个常微分方程模型，一个带有时滞的模型.尽管其中的常微分方程模型与肺结核的实际传染情况有所偏差（修改了四维模型是为了给后面讨论时滞模型提供方便），通过稳定性的讨论，得到了一个阈值R0，也就是基本再生数；然后在模型中引入了一个离散时滞，它描述了从感染到进一步成为结核患者的时间，即潜伏期.通过分析超越特征方程，得到了地方病平衡点稳定的条件，它只和相关参数有关，而与时滞的具体大小无关.

［1］Busenberg S，Cooke K.Vertically Transmitted Diseases［M］.Berlin：Springer，1993.

［2］Cushing J M.Integro-differential Equations and Delay Models in Population Dynamics［M］.Heidelberg：Springer，1977.

［3］Kuang Y.Delay-differential Equations with Applications in Population Dynamics［M］.NewYork：Academic Press，1993.

［4］Stépán G.Retarded Dynamical Systems：Stability and Characteristic Functions［M］.UK：Longman，1989.

［5］何泽荣，刘炎.一类基于时滞和年龄分布的种群控制问题［J］.系统科学与数学，2010（1）：53-59.He Zerong，Liu Yan.On a control problem for a class of population systems with time delay and age distribution［J］.Journal of System Science and Mathematical Science，2010（1）：53-59.（in Chinese）

［6］刘祥东，王辉，胡志兴，等.一类具有时滞和治愈率的HIV 病理模型的稳定性［J］.生物数学学报，2011（1）：108-116.Liu Xiangdong，Wang Hui，Hu Zhixing，et al.Stability of the model with delay and cure rate for HIV pathology［J］.Journal of Biomathematics，2011（1）：108-116.（in Chinese）

［7］Castillo-Chavez C，Feng Z.Totreat or not to treat the case of tuberculosis［J］.J.Math.Biol.，1997，35：629-656.

［8］Andersion R M，May R M.Population biology of infectious diseases：Part 1［J］.Nature，1979，280：361-367.

［9］Bellman R，Cooke K L.Differential-Difference Equations［M］.New York：Academic Press，1963.

［10］Culshaw R V.Mathematical Models of Cell-to-Cell and Cell-Free Viral Spread of HIV infection［D］.Halifax Canada：Dalhousie University，1997.

［11］Dieudonne J.Foundations of Modern Analysis［M］.New York：Academic Press，1960.