基于模糊补偿的弹药自动装填机器人滑模控制

李郁峰，李魁武，潘玉田，郭保全

（1.中北大学 计算机与控制工程学院，山西 太原 030051；2.西北机电工程研究所，陕西 咸阳 712099）

0 引言

众所周知，机械手面临很多不确定性因素的影响，例如摩擦力、扰动力、负载变化大以及建模误差等.仅仅依靠机器人动力学模型的控制算法很难获得预期的控制性能.为了克服这些困难，文献［1］提出了一种基于模糊补偿器的自适应控制算法，在文献［2］中利用了一种基于力矩计算的模糊补偿控制器，文献［3-6］利用一种自适应模糊补偿方法对关节的摩擦力进行了补偿，都取得了一定的效果.近年来，滑模变结构控制被广泛应用到机器人控制中，但是单一的滑模控制有很多缺陷.为了克服这些不足，本文将鲁棒自适应模糊系统与滑模控制相结合，利用自适应模糊系统抑制各种不确定性干扰因素的影响，消除了抖振，减小了跟踪误差.

1 弹药自动装填机器人动力学模型

弹药自动装填机器人如图1 所示，q1和q2为关节角位置，r1和r2分别为大臂和小臂的长度.利用拉格朗日方法可求出其动力学模型为［7］

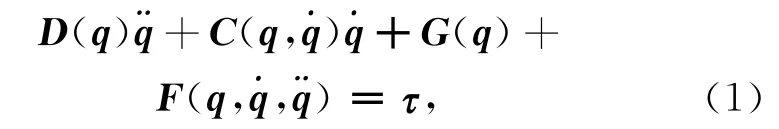
式中：q＝［q1，…，qn］T为n×1维关节位移向量；为n×1维关节速度向量；为n×1维关节加速度向量；D（q）为n×n惯性矩阵；为n×n向心力和哥氏力矩；G（q）为n×1 维重力向量；τ为控制输入向量.是由摩擦力Fr，负载变化和扰动τd的不确定项组成的.

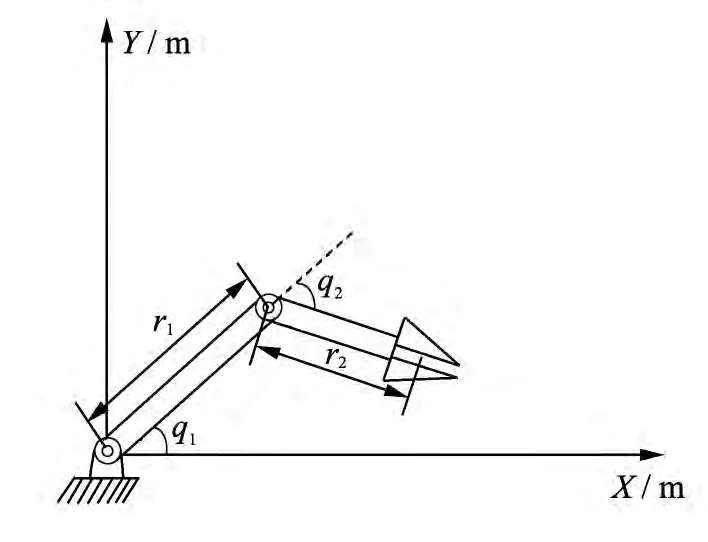
图1 弹药自动装填机器人Fig.1 Ammunition auto-loading manipulator

机器人动力系统具有如下动力学特性［8］：①惯性矩阵M（q）是对称正定阵且有界；②是一个斜对称矩阵，即对任一向量x，则；③重力项满足G（q）≤gb，gb为q的函数.

2 机器人传统滑模控制

弹药自动装填机器人轨迹跟踪的控制目标就是要求关节角位移向量q尽可能好地跟踪期望关节角位移向量qd.

定义跟踪误差

设计滑模面

式中：λ＝diag［λ1，…，λi，…，λn］，为正的对角矩阵.

通过选择控制输入实现对控制目标的控制，滑模面必须满足条件其中ηi为正常数，表明滑模面的能量随着滑模面的衰减而不为零.为了设置控制输入τ，定义参考状态为取控制输入

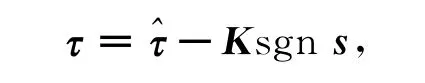
其中：

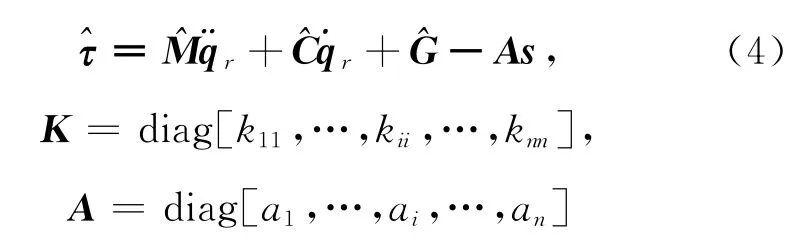
都为正定矩阵，kii和ai都为正常数.于是可得

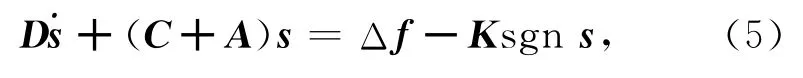
其中：

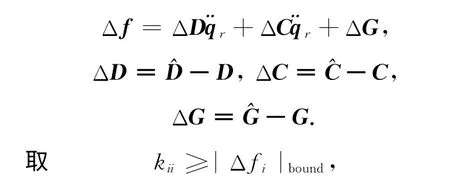
其中｜Δfi｜bound是｜Δfi｜的边界，下面证明整个系统趋于稳定.

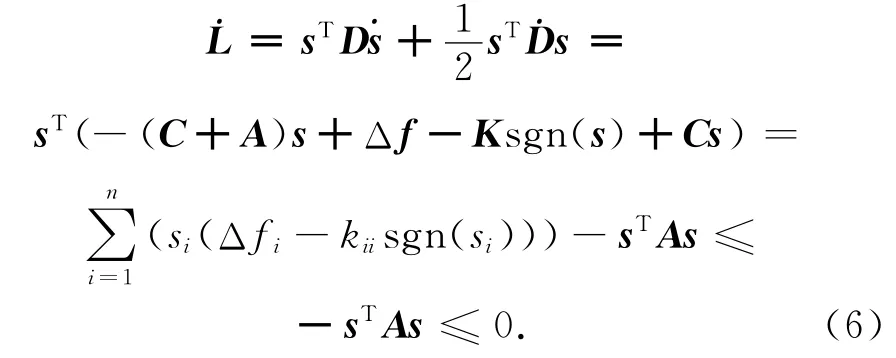
由式（4）知，能够确保滑模面能量随着滑模面衰减而不为零，满足条件.

3 自适应模糊补偿滑模控制

取李雅普诺夫函数

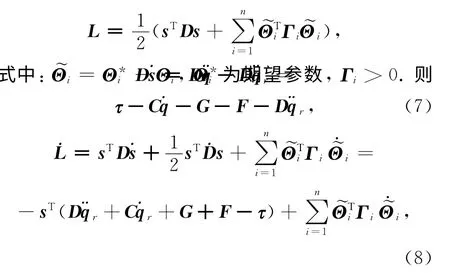
机器人不确定部分同时包括摩擦、外加干扰和负载变化，由于负载变化与速度有关，则将用于逼近不确定项的模糊系统进行分解，可得机器人的动态方程为

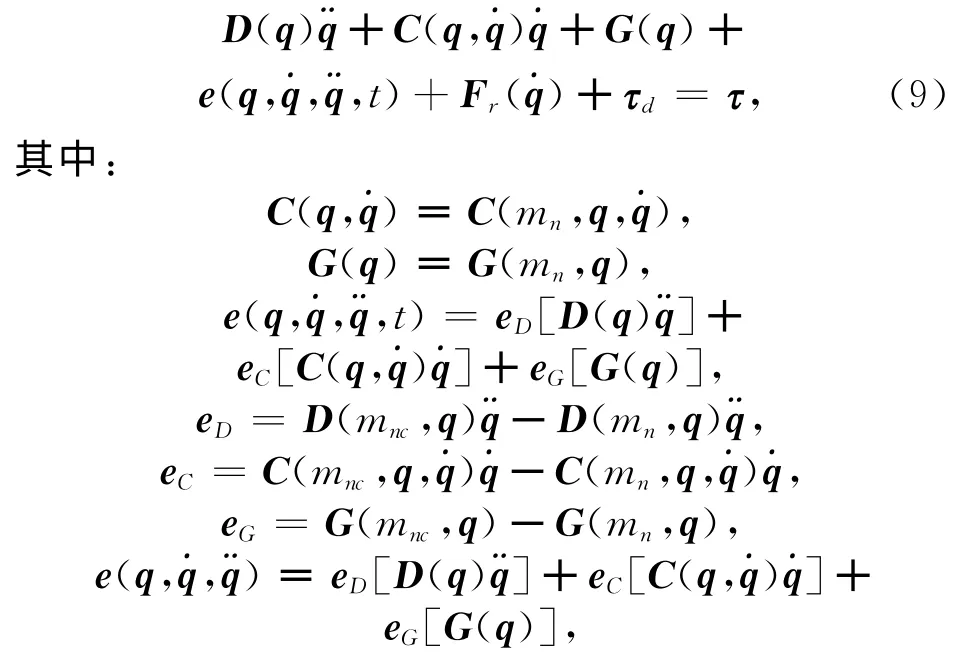
式中：mn为已知的名义值；mnc为实际值.则不确定部分可表示为

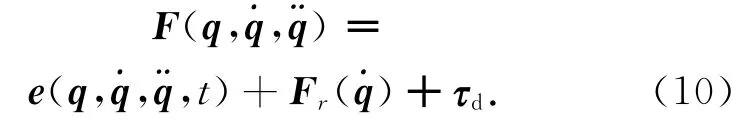
式（10）可分解为

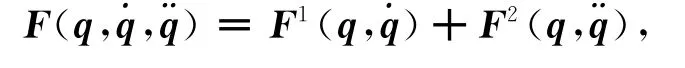
其中：

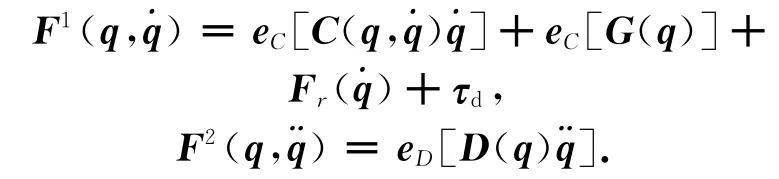
设计鲁棒自适应模糊滑模控制器为

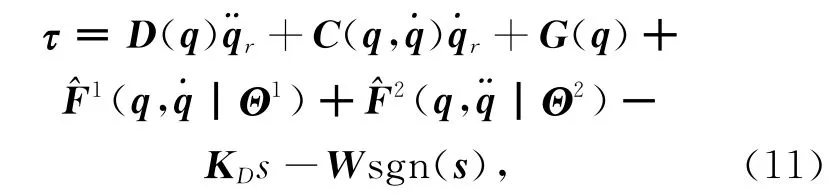
其中：

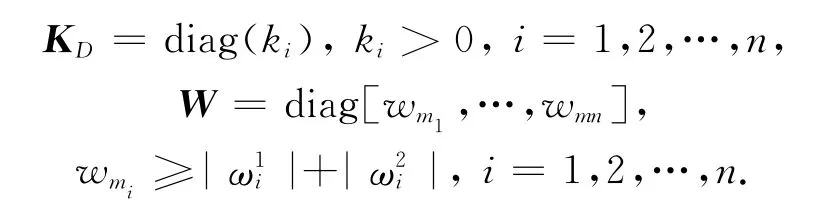
设计自适应律为

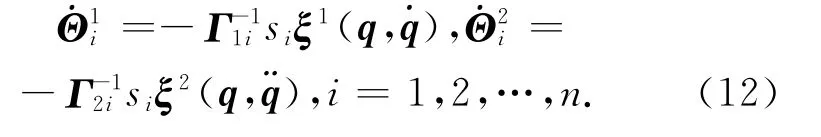
取Lyapunov函数为

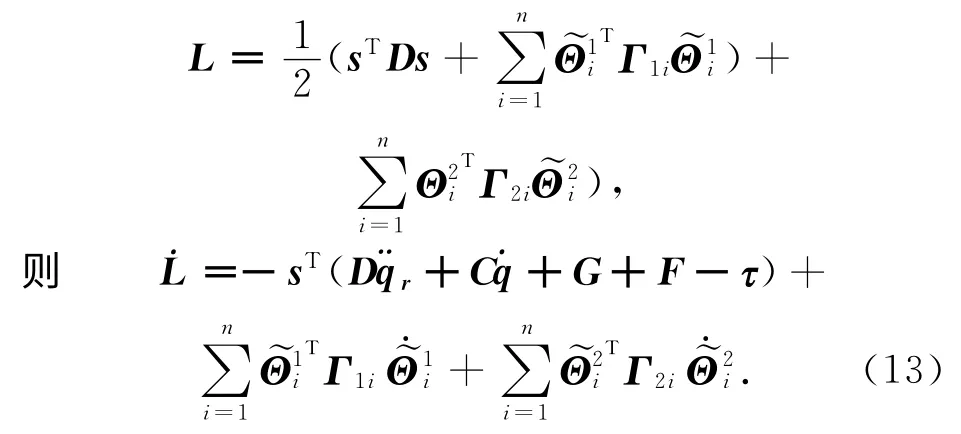
模糊逼近误差分别为

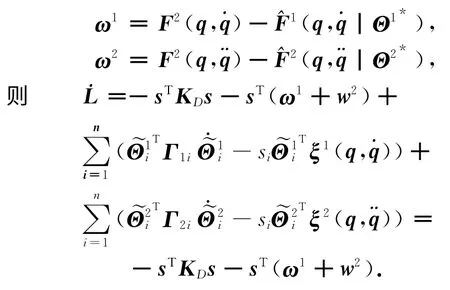
模糊系统设计为

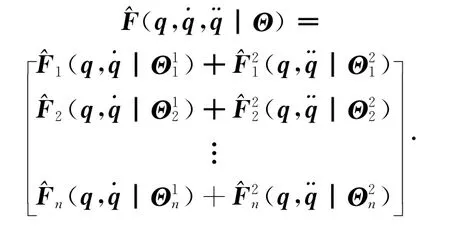
4 仿真实验

针对双关节刚性弹药自动装填机械手，其动力学方程由式（1）可具体表达为［9］

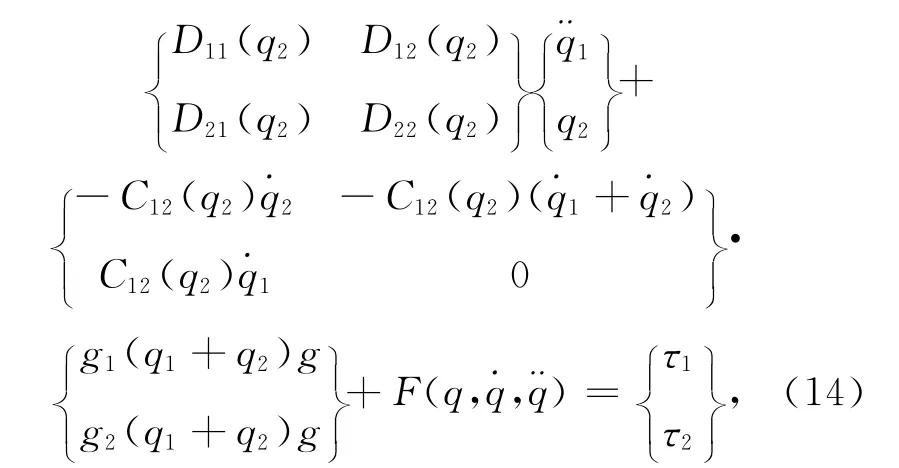
其中：

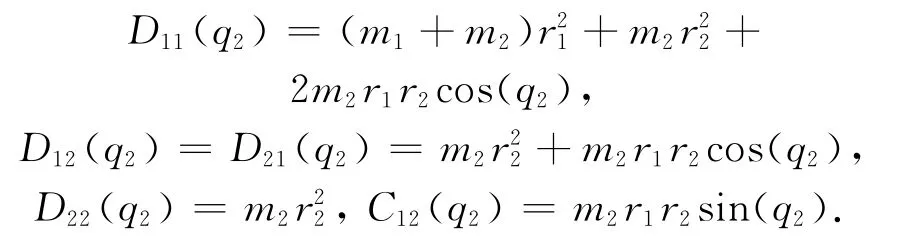
式中：m1和m2分别为连杆1和连杆2的质量；r1和r2分别为大臂和小臂的长度.令

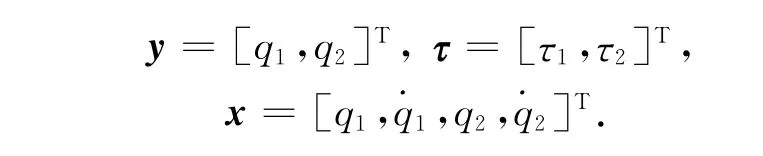
取r1＝1 m，r2＝8 m，m1＝1kg，m2＝1.5kg.控制目标是使两关节的输出q1，q2分别跟踪期望轨迹yd1＝0.3sint和yd2＝0.3sint.隶属函数如图2 所示，定义为

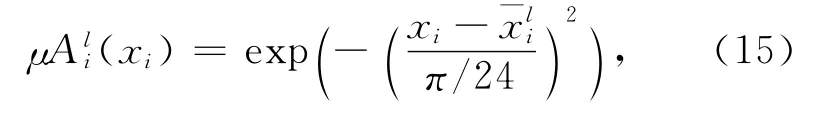
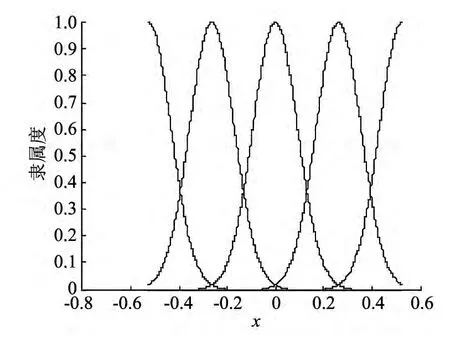
图2 隶属函数图Fig.2 Membership function

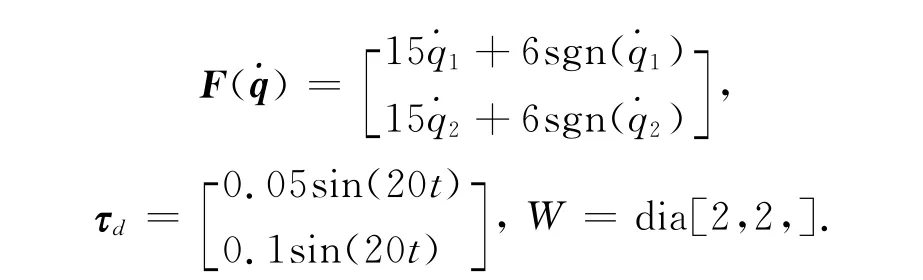
将传统滑模控制与带有自适应模糊补偿的模糊滑模控制分别应用到带有摩擦力、外加干扰力和负载变化的弹药自动装填机器人上，仿真结果如图3～图7 所示.在图3 和图4 中，带有自适应模糊补偿的模糊滑模控制器轨迹跟踪精度明显高于传统滑模控制器.在图5 的速度跟踪图中，本算法要比传统方法误差更小，同时也减小了抖振.在图6 中，本算法有效地解决了力矩控制输入的抖振问题.图7 为摩擦力、外加干扰力和负载变化不确定部分的逼近曲线，减小了不确定部分的影响.

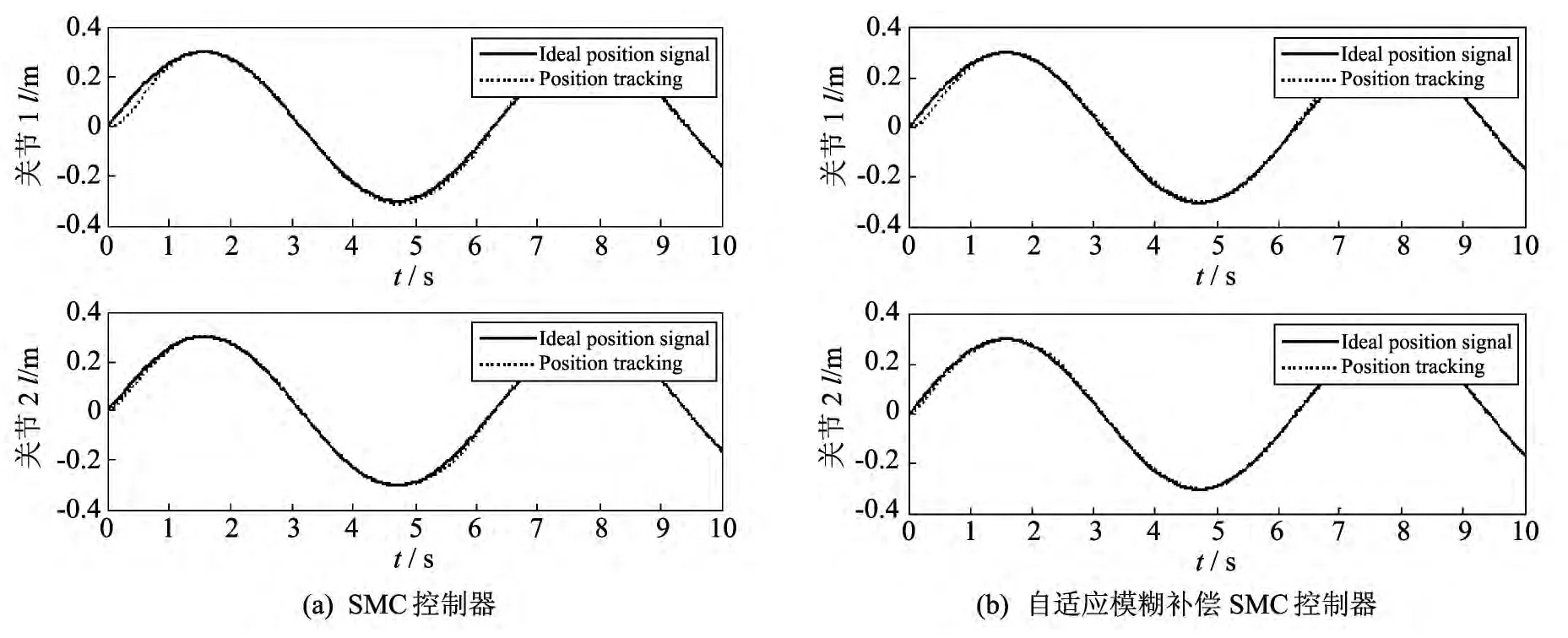
图3 关节1和关节2的位置跟踪Fig.3 Position tracking of joints 1and 2

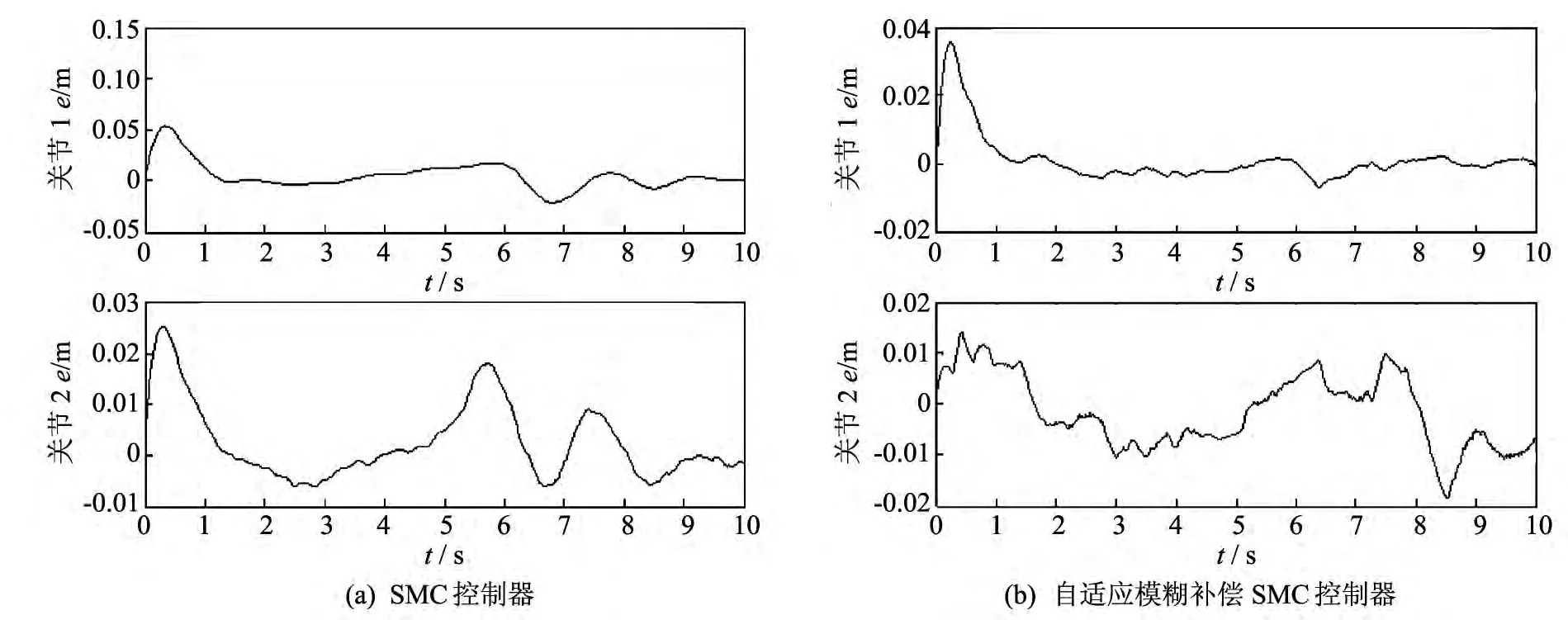
图4 关节1和关节2的位置跟踪误差Fig.4 Position tracking error of joints 1and 2

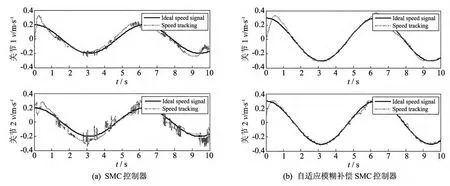
图5 关节1和关节2的速度跟踪Fig.5 Speed tracking of links 1and 2

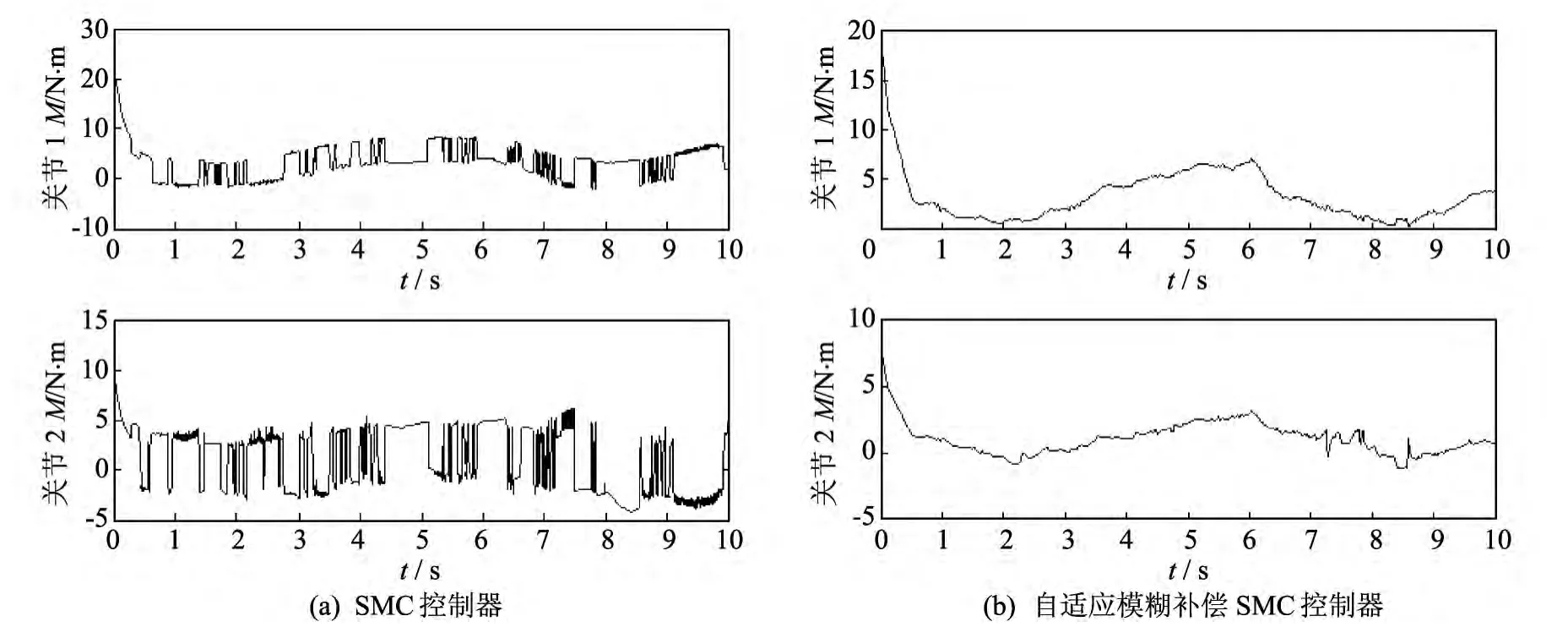
图6 关节1和关节2的力矩控制输入Fig.6 Control torque inputs of links 1and 2

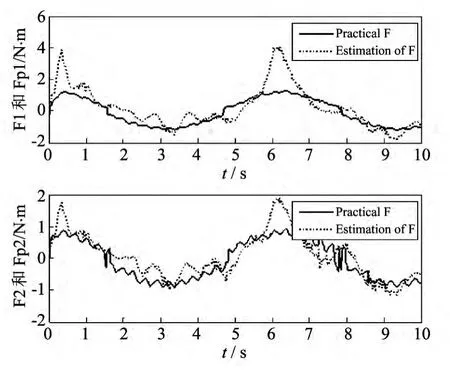
图7 关节1和关节2的不确定部分补偿Fig.7 Uncertain part＇s fuzzy compensation of links 1and 2

5 结论

本文利用自适应模糊系统对外界不确定性扰动、摩擦力的非线性部分、参数变化以及建模误差等不确定部分进行了有效补偿，能够较好地减轻由于不确定部分因素对系统控制性能的影响，消除了传统变结构控制器所固有的抖振现象，减小了跟踪误差，系统性能指标有了明显提高，具有良好的动态性能和稳定鲁棒性，满足了弹药自动装填机器人的性能要求.

［1］Yoo B K，Ham W，C.Adaptive control of robot manipulator using fuzzy compensator［J］.IEEE Transactions on Fuzzy Systems，2000，8（2）：186-199.

［2］Song Zuoshi，Yi Jianqiang，Zhao Dongbin.A computed torque contr-oller for uncertain robotic manipulator systems：fuzzy approach［J］.Fuzzy Sets and Systems，2005，154（3）：208-226.

［3］Chen J S.A robust friction control scheme of robot manipulators［J］.Proceedings of IEEE International Conference on Robotics and Automation，2003，3：345-567.

［4］Kim E.Output feedback tracking control of robot manipulators with model uncertainty via adaptive a fuzzy logic［J］.IEEE Tran.Fuzzy Syst.，2004，12：368-378.

［5］Wang Yongfu，Chai Tianyoui.Compensating modeling and control of robot joint friction based on adaptive fuzzy systems［J］.Chinese Journal of Scientific Instrument，2006，27（2）：186-190.

［6］Ohri J，Dewan L，Soni M K.Fuzzy adaptive dynamic friction compensator for robot［J］.International Journal of Systems Applications，Engineering ＆ Development，2008，4（2）：157-161.

［7］Seul J，Hsia T C.Neural network impedance force control of robot manipulator［J］.IEEE Transactions on Industrial Electronics，1998，45（3）：451-461.

［8］申铁龙.机器人鲁棒控制基础［M］.北京：清华大学出版社，2000.

［9］刘金琨.机器人控制系统的设计与Matlab仿真［M］.北京：清华大学出版社，2008.