一类具有Allee效应的传染病模型时空斑图分析
李桂花,李高峰
(1.中北大学 理学院,山西 太原 030051;2.西南大学 数学与统计学院,重庆 400715;3.新疆农二师库尔勒医院,新疆 库尔勒 841000)
0 引言
寄生虫依靠宿主而生活,它对宿主的影响是多方面的,它或者摄取宿主的营养,对附着组织产生损害,从而影响宿主的生长;或者改变宿主的行为,增加发病率,使宿主易于被捕食者捕食;或者使宿主不能获得充分的生存资源.在种群水平上就是对宿主种群的内禀增长率产生影响,这种影响与寄生虫的感染丰度和频率分布密切相关.
寄生虫从一个宿主传播到另外一个宿主通常是通过自由生活的感染期而取得的.在这种情况下,潜在的宿主和感染期的寄生虫遭遇的机会无疑会受到宿主和寄生虫密度以及它们的空间分布的影 响[1-2].R.M.Anderson,P.J.Whitefied 和A.P.Dobson[3]研究了寄生在体表的复殖吸虫感染期密度对该寄生虫的传播动态的影响.R.M.Anderson[4]研究了穿透表皮的寄生虫感染期的密度对传播动态的影响.A.E.Keymer,R.M.Anderson[5]和A.E.Keymer[6]研究了通过消化道而获得感染的寄生虫的传播过程,其研究表明感染期的寄生虫的密度和空间分布、宿主密度、宿主和寄生虫接触的长短等因素都影响着寄生虫的传播过程.
A.E.Keymer[7]在实验条件下证实了Hymenolepis Diminuta 的囊尾蚴有调节Tribolium Confusum 种群密度的作用.R.M.Anderson和J.Crombie[8]证实了曼氏血吸虫Schistosoma Mansoni的幼虫阶段具有调节中间宿主种群的作用.R.M.Anderson,P.J.Whitefield和C.A.Mills[9]在实验室条件下研究了外寄生虫吸虫的种群动态,对于各种种群参数都进行了详细的研究,其中大量的种群过程是密度制约的.
R.M.Anderson在文献[10]中提出一个数学模型,考虑宿主染病是与自由寄生虫v的接触有关,这里易感者宿主的疾病发生率是双线性的,但是许多实验表明这个疾病的发生率是与寄生虫的剂量有关的,且常常是具有S形的非线性函数,于是R.R.Regoes等[11]建立了下面的模型:

式中:A0表示易感者宿主的输入量;d表示宿主的自然死亡率;β为染病的比例系数;ε为因寄生虫引起的死亡率;c为染病宿主体内自由病毒的释放率;u为寄生虫的死亡率;g(v)是寄生虫浓度v的S形函数,且
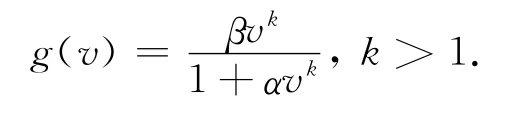
这里β=α=1/mk,m表示染病的剂量;k为S形曲线在点m处的倾角.表明系统(2)在阈值条件下存在两个正平衡点,且一个是不稳定的,另一个是稳定的.当k连续变化时,Li Guihua等[12]发现会有更有趣的更复杂的性态发生(见文献[12]).假设寄生虫的动力学行为比染病者宿主的动力学行为快的多,即u≫δ.令V=uv,则模型(2)为
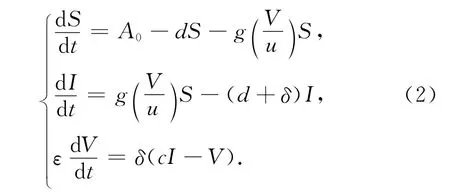
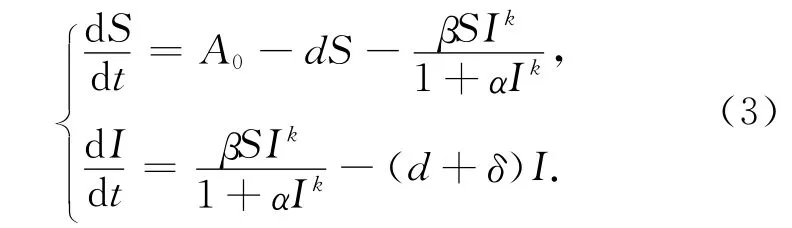
本文将考虑k=1和k=2时空间效应对模型(3)性态的影响,模型如下:
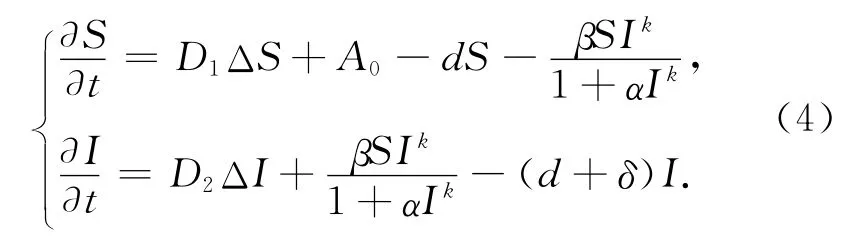
式中:D1,D2分别为易感者宿主S与染病者宿主I的扩散系数.
1 线性稳定性分析
为了简便,将系统(4)作无量纲变换,令
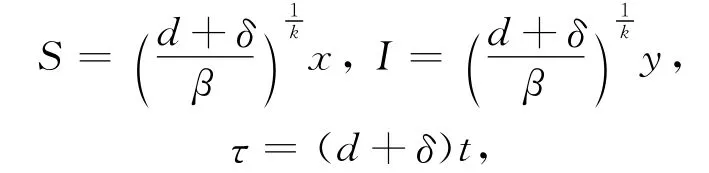
并用t代替τ,得到系统(4)的等价系统
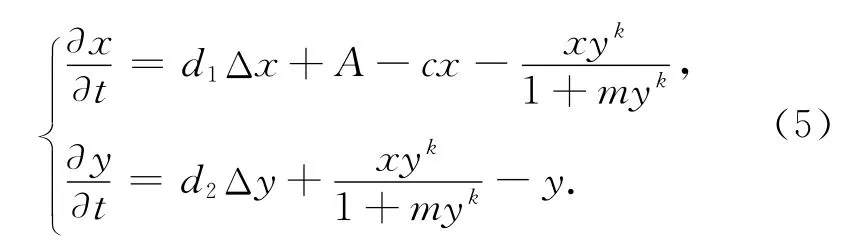
这里:
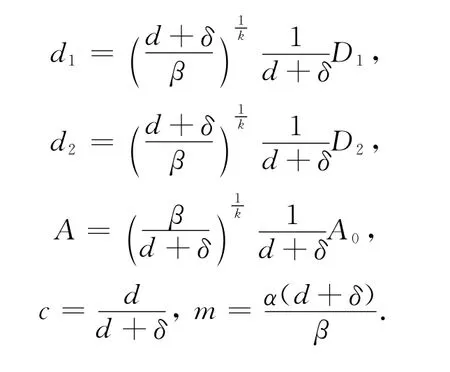
首先考虑最简单的形式,即k=1时系统(5)的动力学性态.当d1=d2=0时,系统(5)的正平衡点存在性及稳定性如下:
定理1 若A>c,则系统(5)存在惟一正均匀定态解
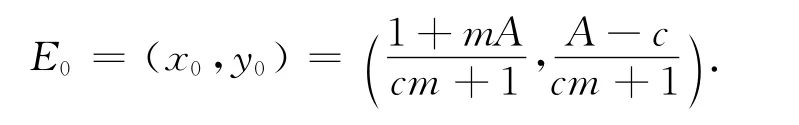
由文献[12]可知,正平衡点只要存在,就一定是全局渐近稳定的.为了分析图灵不稳定的条件,首先计算微扰方程的系数

由于a11,a22始终是小于0,很显然a11d2+a22d1<0.这样由特征方程很容易知道,系统的特征值始终为负,即系统(5)的正均匀定态解是稳定的,不存在图灵分岔.
接着考虑k=2时系统(5)的动力学性态.当d1=d2=0时,系统(5)的正平衡点存在性及稳定性如下:
定理2(a)若A2=4c(1+cm),则系统(5)有惟一正均匀定态解,E*=(x*,y*).
(b)若A2>4c(1+cm),则系统(5)存在两个正均匀定态解,E1=(x1,y1),E2=(x2,y2),且y1<y*<y2.
这里
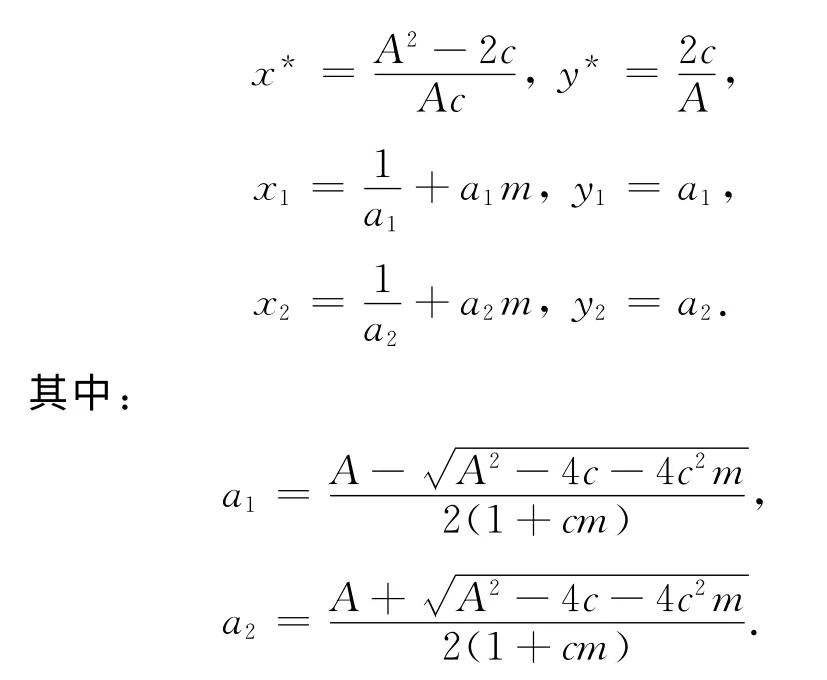
很容易计算当系统存在惟一的均匀定态解时,此均匀定态解为非双曲奇点,其稳定性的计算非常复杂,在这里暂不讨论,仅讨论两个均匀定态解的情形.由文献[12]可知道E1为鞍点,E2为结点或焦点,因此只需要考虑E2附近的微扰分析即可.为了计算上的方便,用a表示a2.
定理3 假定d1=d2=0,且系统(5)存在两个正均匀定态解,则如果下面两个条件之一满足,E2就为渐近稳定的.
(b)1-2c-2c2m>0,且A2(1-c)(1+m+cm)>1+2cm.
系统(5)微扰方程的系数为

因此给出图灵分岔的必要条件为
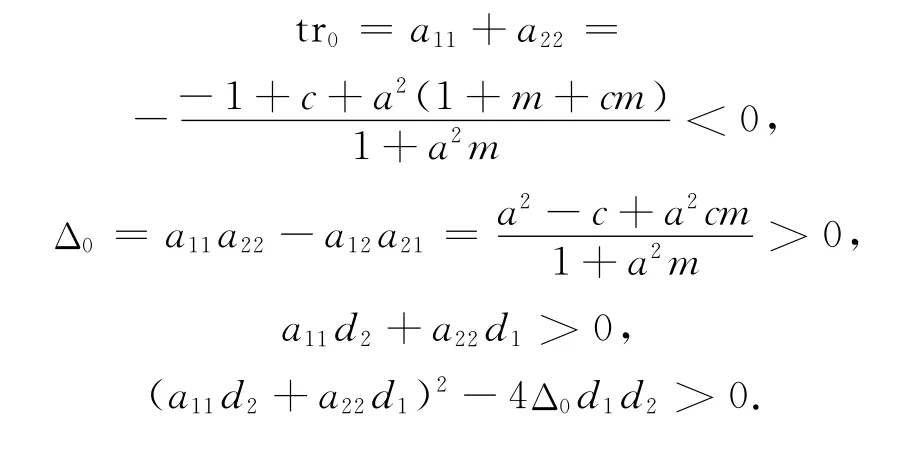
由微扰方程的系数可知a11的值是恒小于零的,根据上面的条件可以得出这样一个结论:如果图灵分岔发生,则一定有a22>0.这意味着易感者宿主对系统起着阻滞子的作用,染病者宿主对系统起着活化子的作用.
Hopf分岔的必要条件为
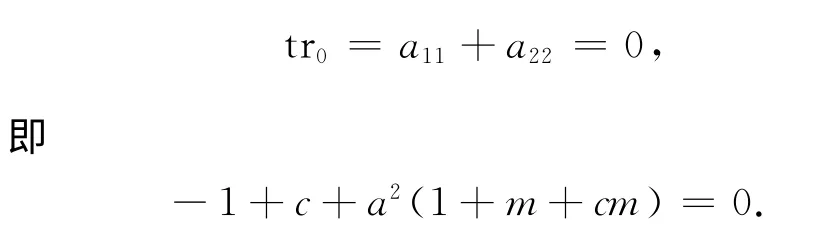
下面分析图灵分岔的稳定性.
2 图灵斑图的稳定性
首先来分析当取定一组具体参数值时,系统发生分岔的区域.设m为分支参数,令d2=1,A=1.2,c=0.2.借助Maple软件计算可以得到当m<4时正均匀定态解存在.图灵分岔发生的首要条件是系统对均匀微扰必须是稳定的,由前面可以知道Δ0>0.只需要计算tr0<0时,m满足的条件即可.通过计算可以知道0 <m<3.884 558 064.当m=3.884 558 064 时,tr0=0,系统存在Hopf分岔.图灵分岔满足的另一个条件是系统对于某些模数的微扰是不稳定的,会出现鞍结点分岔.即系统满足条件
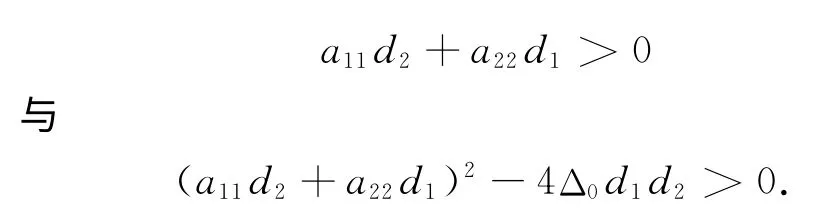
通过分析计算条件,给出了参数m与扩散系数d1的示意图(见图1).参数只有在区域Ⅰ才会出现图灵分岔,在区域Ⅱ与Ⅲ中,图灵分岔条件不满足,但系统稳定与否需要进一步确定.如果固定d1或m,稳定性如何变化,即特征值正负如何呢?若取定d1=15,经计算可以得到m的临界值有两个,分别为m1c=3.322,m2c=0.572 4.当0≤m≤0.572 4或3.322<m<3.884 6时,系统会出现图灵不稳定.从图2 可以看到,当m<0.572 4时,随着m的增加图灵斑图区域逐渐减小(见图2的实线部分);当m>3.322时,随着m的增加,图灵斑图区域逐渐增大(见图2的虚线部分).同时也可以发现m>3.323 的波是m<0.572 4时的波向左平移.
事件,涉及的内容广泛,几乎涵盖了我们生活的方方面面。将事件作为一种营销工具,有具有新闻价值的事件、大型活动、庆典、节事活动等。我们可以将事件营销从规模和类型上进行分类。
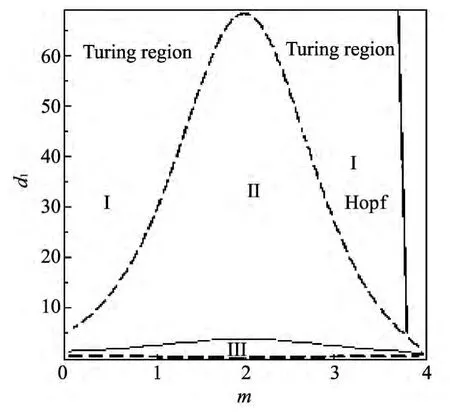
图1 参数m随参数d1的变化图Fig.1 Region graph of parameter mwith d1
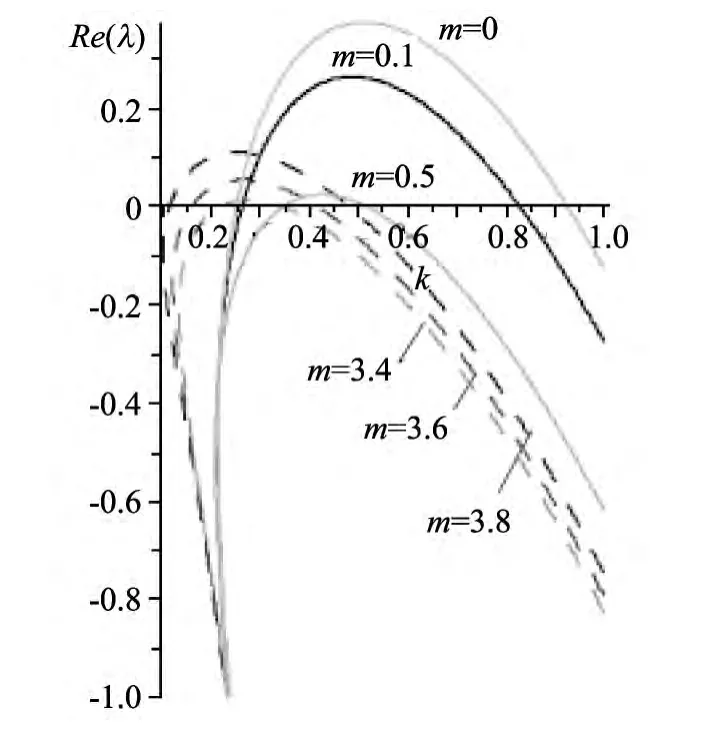
图2 参数m与特征值实部的变化图Fig.2 Graph of parameter mand real part of eigenvalues
3 时空斑图分析
当d1=d2=0时,即常微分(ODE)系统在一定条件下存在两个平衡点,其中染病者宿主密度较小的为鞍点,较大的为结点或焦点.当存在两个正平衡点时,ODE 系统性态可能有下面几种:平衡点稳定,但不存在极限环;平衡点稳定,存在不稳定的极限环;平衡点不稳定,但不存在极限环;平衡点不稳定,存在稳定的极限环.当d1,d2≠0时,即偏微分(PDE)系统性态比较复杂,只考虑稳定与不稳定两种情形.下面取一组固定的值来分析ODE 系统与PDE 系统的可能组合.取d1=15,d2=1,A=1.2,c=0.2,具体组合见表1.在此的稳定性指正均匀稳态解的稳定性.
作者发现,当取上面这组值时,有些组合还没有,因此取另一组值d2,A,c不变,d1=3,具体组合见表2.由表1 和 表2 发现,系统存在稳定的极限环的几种形式还不包含,在此不再列出.原因是当ODE系统存在稳定的极限环时,相应的PDE系统是不稳定的,通过数值模拟发现系统出现一般的图灵斑图,没有什么新的现象发生.
下面分别对上面几种情形进行模拟,看m处在不同区域时,系统的动力学性态如何,性态是否有规律可循.从表1 直观分析系统的性态,可以得到情形1 和情形3 都属于ODE 系统平衡点稳定且不存在极限环,而相应的PDE 系统是不稳定的,因此可以知道系统满足图灵不稳定的条件.在这几种情形下图灵斑图发生,图灵斑图究竟是什么形状呢?下面利用第2部分的有限差分方程的方法来进行数值模拟.对于表1 中的情形1,分别取m=0,0.1,0.3,0.5进行模拟.

表1 当d1=15,d2=1,A=1.2,c=0.2时,ODE与PDE系统动力学性态分类Tab.1 The different dynamic behaviors of ODE and PDE systems when d1=15,d2=1,A=1.2,c=0.2

表2 当d1=3,d2=1,A=1.2,c=0.2时,ODE与PDE系统动力学性态分类Tab.2 The different dynamic behaviors of ODE and PDE systems when d1=3,d2=1,A=1.2,c=0.2
从图3(a)可以看到,当m=0时,系统的图灵斑图完全是点状的;当m=0.1时,系统基本上是条状斑图.因此可以很自然地想到,m在0与0.1之间连续变化时系统的斑图是逐渐由点状过渡到条状斑图的;当m=0.3时,发现系统的图灵斑图是点条共存的,但是这种斑图与图3(b)的点条共存正好是相反的(见图3(c);当m=0.5时,系统的图灵斑图变为点状的,这种点状斑图与图3(a)的点状也是正好相反的(见图3(d)),被称为缺口状斑图.因此有m在0.1与0.572 4之间连续变化时,系统由前一种的条状图灵斑图逐步变为后一种的条状图灵斑图,然后由条状逐渐变为后一种点状图灵斑图.换句话说,随着染病者剂量m∈(0,0.572 4)由小到大变化,染病者宿主的密度分布由疏到密.
表1 的情形2,对于ODE 与PDE 系统的正均匀平衡解均稳定,这种情形不是本文考虑的重点.对于表1的情形3和情形4,通过数值模拟发现,m在这两个区域内的图灵斑图类似(尽管情形4 中ODE系统存在极限环).分别给出m=3.6与m=3.8 时,系统的斑图(见图4),可以看到图4(b)是缺口状斑图到迷宫斑图的过渡.
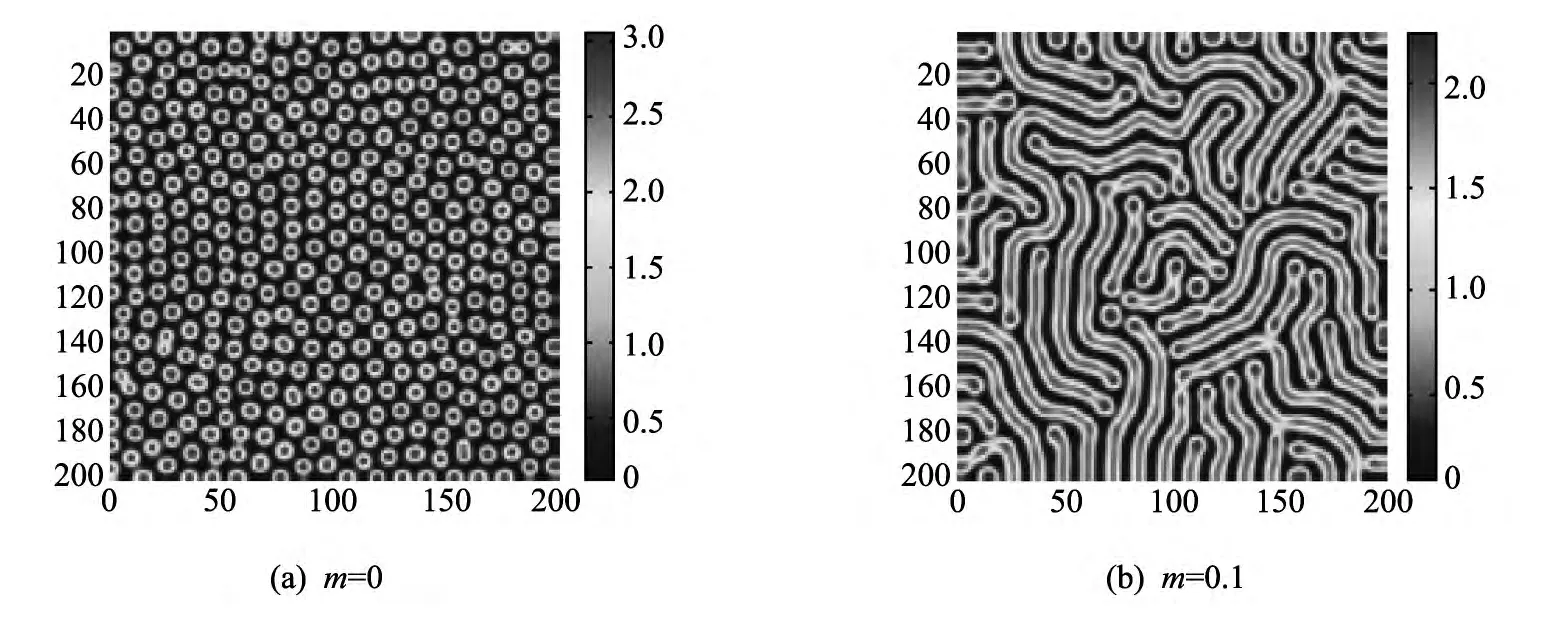
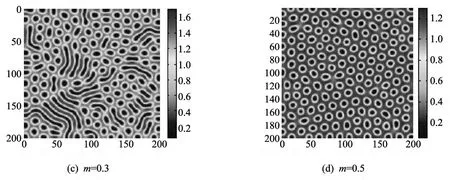
图3 d1=15,d2=1,A=1.2,c=0,2时,系统(5)的图灵斑图Fig.3 Turing pattern of system(5)when d1=15,d2=1,A=1.2,c=0.2
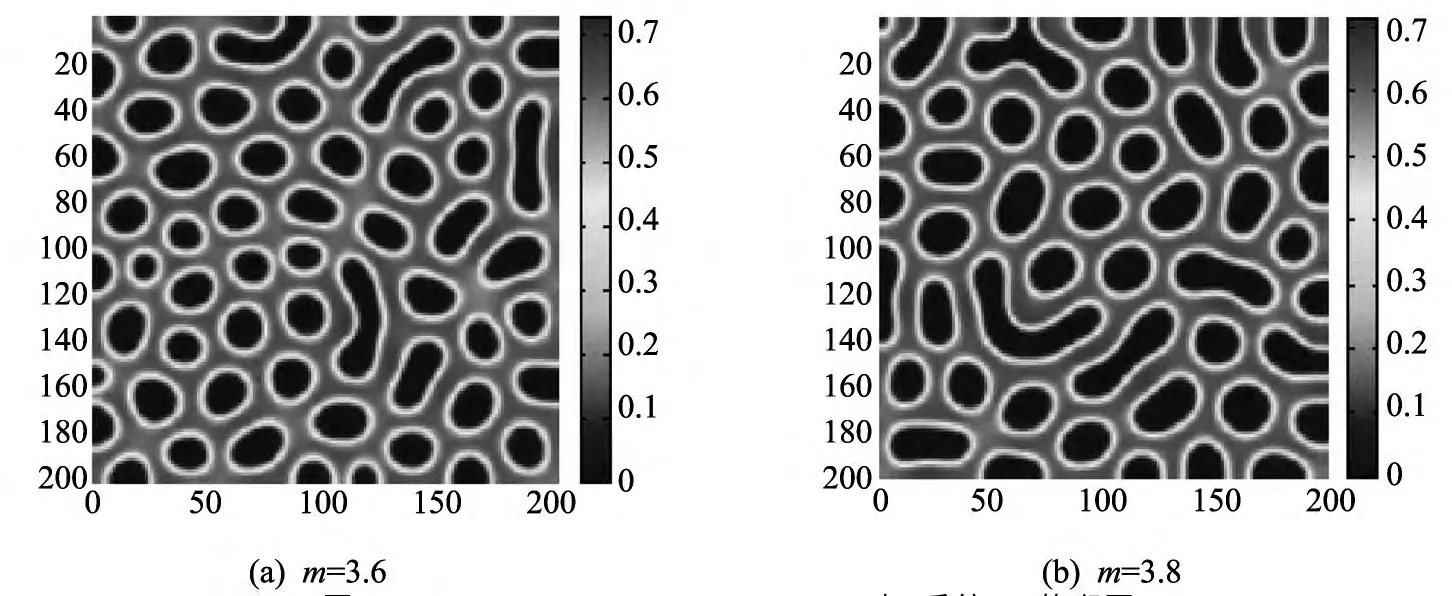
图4 d1=15,d2=1,A=1.2,c=0.2时,系统(5)的斑图Fig.4 Spatial pattern of system(5)when d1=15,d2=1,A=1.2,c=0.2
对于表1 的最后一种情形,取m在这个区间的一个值3.95,其它参数不变.用同样的方法进行数值模拟发现,反应扩散方程出现迷宫斑图,如图5 所示.由文献[13]知道迷宫斑图的形成需要两个必要条件:①系统经历横向失稳;②当两个波峰互相靠近时,它们之间会产生相互排斥作用.这种排斥作用能够使波峰靠近的速度放慢以至最后停止.也就是说,两个波峰不会因合并而湮灭.在此,我们想是不是由于极限环的存在,引起图灵斑图失稳而引起波峰的变化,从而产生迷宫斑图.
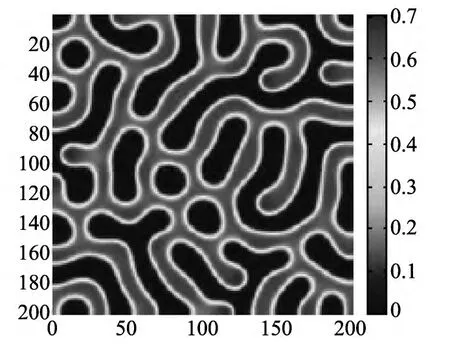
图5 d1=15,d2=1,A=1.2,c=0.2,m=3.95时,系统(5)的迷宫斑图Fig.5 Labyrinth patterns of system(5)when d1=15,d2=1,A=1.2,c=0.2,m=3.95
进一步,对表2中的几种情形分别进行了讨论.第1种情形不做讨论,首先从第2种情形来讨论.对于情形2,与情形1的区别是存在一个不稳定的极限环,就由于这点区别,系统的动力学性态发生了很大的改变.取m=3.8,利用有限差分的方法进行数值模拟发现:在这组参数值下,系统(5)有螺旋波发生(如图6 所示).
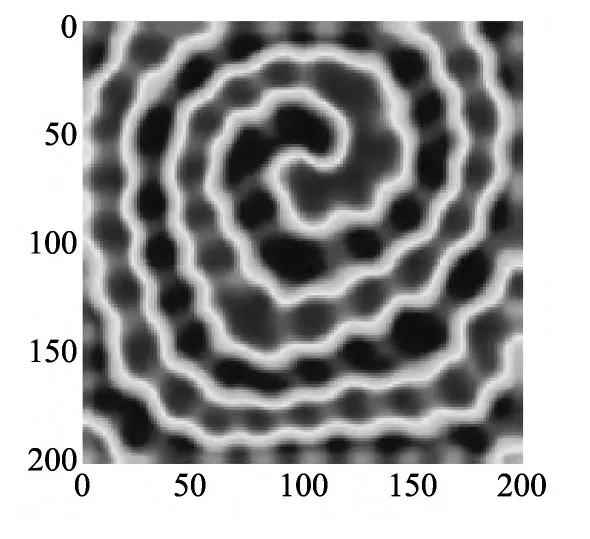
图6 d1=3,d2=1,A=1.2,c=0.2,m=3.8时,系统(5)的螺旋波斑图Fig.6 Spiral waves pattern of system(5)when d1=3,d2=1,A=1.2,c=0.2,m=3.8
对于表2的情形3,发现尽管不存在极限环,但在这个区间上会由共振形成一种静态波,如图7 所示.另外,给出了变量y随时间t的变化图(如图7(b)),发现随着时间的增加,变量y最终趋于一稳态.
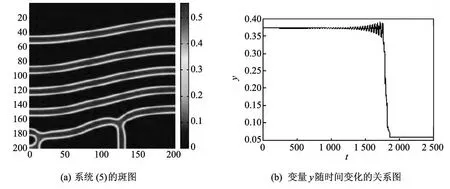
图7 d1=3,d2=1,A=1.2,c=0.2,m=3.9时,系统(5)的斑图与变量y随时间t变化的关系图Fig.7 Spatial patterns of system(5)and relationship diagram of variable y and time twhen d1=3,d2=1,A=1.2,c=0.2,m=3.9
对于情形4,发现在这个区间上会出现迷宫斑图,给出了m=3.95时分别取空间步长为1,时间步长为0.05,运行1万次和10万次时斑图的变化情况(见图8).由图8 可以发现,随着时间的增加,染病者宿主的分布逐渐变得稀疏.另外,从表2 的这几种情形分析,将宿主的扩散率固定在某一数值时,随着染病者剂量函数m的由小变大,系统(5)的斑图由行波、静态波到迷宫斑图.

图8 d1=3,d2=1,A=1.2,c=0.2,m=3.95时,系统(5)的迷宫斑图Fig.8 Labyrinth patterns of system(5)when d1=3,d2=1,A=1.2,c=0.2,m=3.95
通过上面的数值模拟可以发现,螺旋波的出现是由于扩散率的变化引起的,因此考虑扩散率的变化对系统斑图的变化是非常自然的事情.固定m=3.8来分析扩散系数d1的变化,动力学性态会有什么改变.当m=3.8,A=1.2,c=0.2,d2=1时,常微分系统始终存在一不稳定的极限环.分别取d1=0.1,0.5,1,3,3.5,4,利用有限差分法进行数值模拟(如图9),其中(a)~(e)为典型的螺旋波斑图,(f)为混沌斑图.
由图9 可以发现,当d1=0.1,1,3.5时,系统中的缺陷数目有多个;当d1=0.5,3时,系统中的缺陷数目只有一个;当d1=4时,发现螺旋波失稳导致时空混沌(见图9(f));继续增大d1,化为表1的第4种情形.我们知道螺旋波是由缺陷为中心自组织形成的一类特殊的行波,对于一个稳定的螺旋波斑图态,系统中的缺陷(或缺陷密度)很少,并且他们的数目不随时间变化.但是,如果系统中的控制变量超过某些临界值时,螺旋波会自发地产生出新的缺陷,而每个缺陷都趋向于产生新的螺旋波.因此,系统中的缺陷数目会随着时间以指数的形式增加,直到系统达到一个饱和的缺陷密度.此时系统中被缺陷充满,它的长期有序现象不复存在,系统进入时空混沌态.
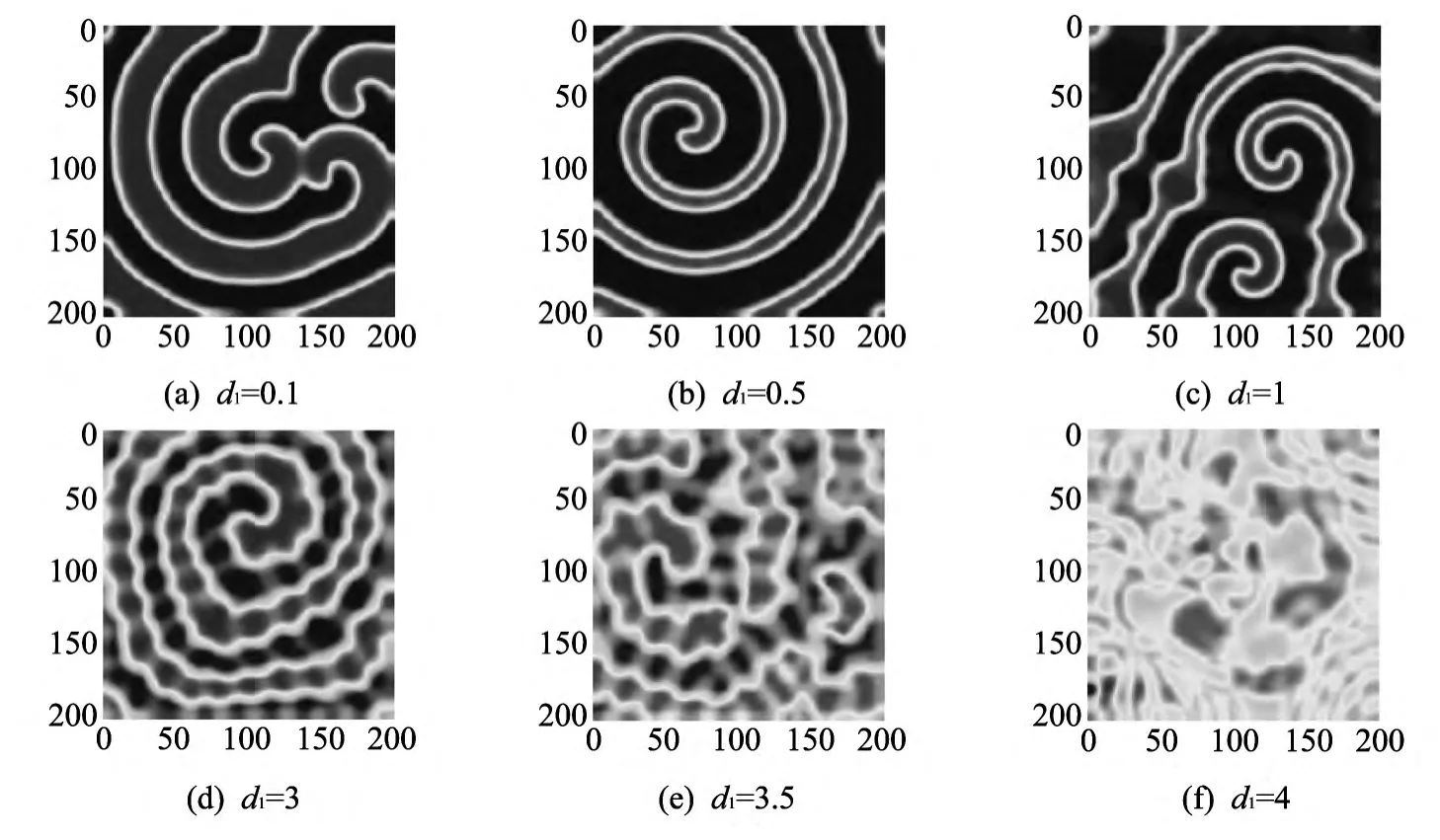
图9 不同d1,d2=1,A=1.2,c=0.2,m=3.8 时,系统(5)螺旋波的不同斑图Fig.9 Different spiral waves patterns of system(5)when different d1,d2=1,A=1.2,c=0.2,m=3.8
4 讨论
讨论了当k=1 和k=2 时系统(5)的时空斑图.当k=1时,系统始终是稳定的,不会发生图灵斑图;当k=2时,根据系统稳定性及极限环的存在性进行了分类.发现一些非常有趣的现象,当ODE系统稳定,且不存在极限环相应的PDE系统不稳定时,则PDE 系统出现图灵斑图,且图灵斑图可能有两种形式,每种形式包括点状与条状斑图.若ODE系统存在一不稳定的极限环,而PDE系统是稳定的话,出现螺旋波.若ODE 系统尽管不存在极限环,但平衡点是不稳定的,而PDE系统是稳定的时,系统同样会出现行波,但这种行波是静态的.若ODE 系统不存在极限环,但平衡点是不稳定的,而PDE 系统也是不稳定的时,则系统出现迷宫斑图.通过数值模拟猜测这种规律是可循的.在本文中,由于时间的关系,仅考虑了一种特殊形式的系统的性态,即k=2.若对于k取更大的值,PDE系统的性态可能更复杂,详细分析可以查阅文献[14].
关于考虑空间因素的传染病模型的研究,已有一些文献,有考虑一般传染病模型(见文献[15-16]),有考虑具体疾病的模型(见文献[17-18]).若考虑空间因素还可以应用到各个领域,比如生态环境等(见文献[19]).另外,考虑反应扩散的传染病模型还有很多文献,在此不一一列出.
[1]Crofton H D.A quantitative approach to parasitism[J].Parasitology,1971,62:179-194.
[2]Anderson R M.The regulation of host population growth by parasitic speies[J].Parasitology,1978,76:119-157.
[3]Anderson R M,Whitefield P J,Dobson A P.Experimental studies of infection dynamics:infection of the definitive host by the cercariae of transversotrema patialense[J].Parasitology,1978,77:189-200.
[4]Anderson R M.Population dynamics of snail infection by microcidia[J].Parasitology,1978,77:201-224.
[5]Keymer A E,Anderson R M.The dynamics of infection of tribolium confusum by hymenolopis diminuta:the influence of infective-stage density and spatial distribution[J].Parasitology,1979,79:195-207.
[6]Keymer A E.The dynamics of infection of tribolium confusum by hymenolopis diminuta,the influence of exposure time and host density[J].Parasitology,1982,84:157.
[7]Keymer A E.Population dynamics of hymenolepis diminutain the intermediate host[J].Journal of Animal Ecology,1981,50:941-950.
[8]Anderson R M.Experimental studies of age-prevalence curves of schistosoma mansoni infection in populations of biomphalaria glabrata[J].Parasitology,1984,89:79-104.
[9]Anderson R M,Whitefield P J.An experimental study of the population dynamics of anectoparasitic digenean transversotrema patialense(soparker):cercarial and adult stages[J].Journal of Animal Ecology,1977,46:555-580.
[10]Anderson R M,May R M.The population dynamics of microparasites and their invertebrate hosts[J].Phil.Trans.R.Soc.Lond.B,1981,291:451-524.
[11]Regoes R R,Ebert D.Dose-dependent infection rates of parasites produce the allee effectin epidemiology[J].Proc.R.Soc.Lond.B,2002,269:271-279.
[12]Li Guihua.Bifurcation analysis of an epidemic model with nonlinear incidence[J].Applied Mathematics and Computation,2009,214(2):411-423.
[13]Britton N F.Essential Mathematical Biology[M].London:Springer,2003.
[14]李桂花,王稳地.传染病动力学模型性态分析[D].西南大学,2008.
[15]Wang Weiming,Cai Yongli.Complex dynamics of a reaction-diffusion epidemic model[J].Nonlinear Analysis:Real World Applications,2012,13(5):2240-2258.
[16]Sun Guiquan,Jin Zhen,Liu Quqnxing,et al.Pattern formation in a spatial S-I model with non-linear incidence rates[J].J.Stat.Mech.,2007,11:11011.
[17]Wang K,Wang W,Song S.Dynamics of an HBV model with diffusion and delay[J].J.Theoret.Biol.,2008(1):36-44.
[18]Xu R,Ma Z.An HBV model with diffusion and time delay[J].J.Theoret.Biol.,2009,257(3):499-509.
[19]Sun Guiquan,Li Li,Wang Zike.Spatial dynamics of a vegetation model in an arid flat environment[J].Nonlinear Dynamics,2013,73(4):2207-2219.

